Polarization identity
In linear algebra, a branch of mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. If a norm arises from an inner product then the polarization identity can be used to express this inner product entirely in terms of the norm. The polarization identity shows that a norm can arise from at most one inner product; however, there exist norms that do not arise from any inner product.
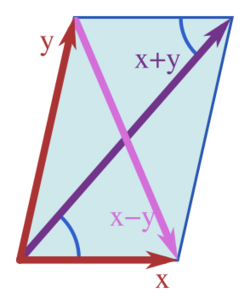
The norm associated with any inner product space satisfies the parallelogram law: [math]\displaystyle{ \|x+y\|^2 + \|x-y\|^2 = 2\|x\|^2 + 2\|y\|^2. }[/math] In fact, as observed by John von Neumann,[1] the parallelogram law characterizes those norms that arise from inner products. Given a normed space [math]\displaystyle{ (H, \|\cdot\|) }[/math], the parallelogram law holds for [math]\displaystyle{ \|\cdot\| }[/math] if and only if there exists an inner product [math]\displaystyle{ \langle \cdot, \cdot \rangle }[/math] on [math]\displaystyle{ H }[/math] such that [math]\displaystyle{ \|x\|^2 = \langle x,\ x\rangle }[/math] for all [math]\displaystyle{ x \in H, }[/math] in which case this inner product is uniquely determined by the norm via the polarization identity.[2][3]
Polarization identities
Any inner product on a vector space induces a norm by the equation [math]\displaystyle{ \|x\| = \sqrt{\langle x, x \rangle}. }[/math] The polarization identities reverse this relationship, recovering the inner product from the norm. Every inner product satisfies: [math]\displaystyle{ \|x + y\|^2 = \|x\|^2 + \|y\|^2 + 2\operatorname{Re}\langle x, y \rangle \qquad \text{ for all vectors } x, y. }[/math]
Solving for [math]\displaystyle{ \operatorname{Re}\langle x, y \rangle }[/math] gives the formula [math]\displaystyle{ \operatorname{Re}\langle x, y \rangle = \frac{1}{2} \left(\|x+y\|^2 - \|x\|^2 - \|y\|^2\right). }[/math] If the inner product is real then [math]\displaystyle{ \operatorname{Re}\langle x, y \rangle = \langle x, y \rangle }[/math] and this formula becomes a polarization identity for real inner products.
Real vector spaces
If the vector space is over the real numbers then the polarization identities are:[4]
[math]\displaystyle{ \begin{alignat}{4} \langle x, y \rangle &= \frac{1}{4} \left(\|x+y\|^2 - \|x-y\|^2\right) \\[3pt] &= \frac{1}{2} \left(\|x+y\|^2 - \|x\|^2 - \|y\|^2\right) \\[3pt] &= \frac{1}{2} \left(\|x\|^2 + \|y\|^2 - \|x-y\|^2\right). \\[3pt] \end{alignat} }[/math]
These various forms are all equivalent by the parallelogram law:[proof 1]
[math]\displaystyle{ 2\|x\|^2 + 2\|y\|^2 = \|x+y\|^2 + \|x-y\|^2. }[/math]
This further implies that [math]\displaystyle{ L^p }[/math] class is not a Hilbert space whenever [math]\displaystyle{ p\neq 2 }[/math], as the parallelogram law is not satisfied. For the sake of counterexample, consider [math]\displaystyle{ x=1_A }[/math] and [math]\displaystyle{ y=1_B }[/math] for any two disjoint subsets [math]\displaystyle{ A,B }[/math] of general domain [math]\displaystyle{ \Omega\subset\mathbb{R}^n }[/math] and compute the measure of both sets under parallelogram law.
Complex vector spaces
For vector spaces over the complex numbers, the above formulas are not quite correct because they do not describe the imaginary part of the (complex) inner product. However, an analogous expression does ensure that both real and imaginary parts are retained. The complex part of the inner product depends on whether it is antilinear in the first or the second argument. The notation [math]\displaystyle{ \langle x | y \rangle, }[/math] which is commonly used in physics will be assumed to be antilinear in the first argument while [math]\displaystyle{ \langle x,\, y \rangle, }[/math] which is commonly used in mathematics, will be assumed to be antilinear its the second argument. They are related by the formula: [math]\displaystyle{ \langle x,\, y \rangle = \langle y \,|\, x \rangle \quad \text{ for all } x, y \in H. }[/math]
The real part of any inner product (no matter which argument is antilinear and no matter if it is real or complex) is a symmetric bilinear map that for any [math]\displaystyle{ x, y \in H }[/math] is always equal to:[4][proof 1] [math]\displaystyle{ \begin{alignat}{4} R(x, y) :&= \operatorname{Re} \langle x \mid y \rangle = \operatorname{Re} \langle x, y \rangle \\ &= \frac{1}{4} \left(\|x+y\|^2 - \|x-y\|^2\right) \\ &= \frac{1}{2} \left(\|x+y\|^2 - \|x\|^2 - \|y\|^2\right) \\[3pt] &= \frac{1}{2} \left(\|x\|^2 + \|y\|^2 - \|x-y\|^2\right). \\[3pt] \end{alignat} }[/math]
It is always a symmetric map, meaning that[proof 1] [math]\displaystyle{ R(x, y) = R(y, x) \quad \text{ for all } x, y \in H, }[/math] and it also satisfies:[proof 1] [math]\displaystyle{ R(y, ix) = - R(x, iy) \quad \text{ for all } x, y \in H. }[/math] Thus [math]\displaystyle{ R(ix, y) = - R(x, iy), }[/math] which in plain English says that to move a factor of [math]\displaystyle{ i }[/math] to the other argument, introduce a negative sign.
Proof of properties of [math]\displaystyle{ R }[/math]
|
|---|
|
Let [math]\displaystyle{ R(x, y) := \frac{1}{4} \left(\|x+y\|^2 - \|x-y\|^2\right). }[/math] Then [math]\displaystyle{ 2\|x\|^2 + 2\|y\|^2 = \|x+y\|^2 + \|x-y\|^2 }[/math] implies [math]\displaystyle{ R(x, y) = \frac{1}{4} \left(\left(2\|x\|^2 + 2\|y\|^2 - \|x-y\|^2\right) - \|x-y\|^2\right) = \frac{1}{2} \left(\|x\|^2 + \|y\|^2 - \|x-y\|^2\right) }[/math] and [math]\displaystyle{ R(x, y) = \frac{1}{4} \left(\|x+y\|^2 - \left(2\|x\|^2 + 2\|y\|^2 - \|x+y\|^2\right)\right) = \frac{1}{2} \left(\|x+y\|^2 - \|x\|^2 - \|y\|^2\right). }[/math] Moreover, [math]\displaystyle{ 4R(x, y) = \|x+y\|^2 - \|x-y\|^2 = \|y+x\|^2 - \|y-x\|^2 = 4R(y, x), }[/math] which proves that [math]\displaystyle{ R(x, y) = R(y, x). }[/math] From [math]\displaystyle{ 1 = i (-i) }[/math] it follows that [math]\displaystyle{ y-ix = i(-iy-x) = -i(x+iy) }[/math] and [math]\displaystyle{ y+ix = i(-iy+x) = i(x-iy) }[/math] so that [math]\displaystyle{ -4R(y, ix) = \|y-ix\|^2 - \|y+ix\|^2 = \|(-i)(x+iy)\|^2 - \|i(x-iy)\|^2 = \|x+iy\|^2 - \|x-iy\|^2 = 4R(x, iy), }[/math] which proves that [math]\displaystyle{ R(y, ix) = - R(x, iy). }[/math] [math]\displaystyle{ \blacksquare }[/math] |
Unlike its real part, the imaginary part of a complex inner product depends on which argument is antilinear.
Antilinear in first argument
The polarization identities for the inner product [math]\displaystyle{ \langle x \,|\, y \rangle, }[/math] which is antilinear in the first argument, are
- [math]\displaystyle{ \begin{alignat}{4} \langle x \,|\, y \rangle &= \frac{1}{4} \left(\|x+y\|^2 - \|x-y\|^2 - i\|x + iy\|^2 + i\|x - iy\|^2\right) \\ &= R(x, y) - i R(x, iy) \\ &= R(x, y) + i R(ix, y) \\ \end{alignat} }[/math]
where [math]\displaystyle{ x, y \in H. }[/math] The second to last equality is similar to the formula expressing a linear functional [math]\displaystyle{ \varphi }[/math] in terms of its real part: [math]\displaystyle{ \varphi(y) = \operatorname{Re} \varphi(y) - i (\operatorname{Re} \varphi)(i y). }[/math]
Antilinear in second argument
The polarization identities for the inner product [math]\displaystyle{ \langle x, \ y \rangle, }[/math] which is antilinear in the second argument, follows from that of [math]\displaystyle{ \langle x \,|\, y \rangle }[/math] by the relationship: [math]\displaystyle{ \langle x, \ y \rangle := \langle y \,|\, x \rangle = \overline{\langle x \,|\, y \rangle} \quad \text{ for all } x, y \in H. }[/math] So for any [math]\displaystyle{ x, y \in H, }[/math][4]
- [math]\displaystyle{ \begin{alignat}{4} \langle x,\, y \rangle &= \frac{1}{4} \left(\|x+y\|^2 - \|x-y\|^2 + i\|x + iy\|^2 - i\|x - iy\|^2\right) \\ &= R(x, y) + i R(x, iy) \\ &= R(x, y) - i R(ix, y). \\ \end{alignat} }[/math]
This expression can be phrased symmetrically as:[5] [math]\displaystyle{ \langle x, y \rangle = \frac{1}{4} \sum_{k=0}^3 i^k \left\|x + i^k y\right\|^2. }[/math]
Summary of both cases
Thus if [math]\displaystyle{ R(x, y) + i I(x, y) }[/math] denotes the real and imaginary parts of some inner product's value at the point [math]\displaystyle{ (x, y) \in H \times H }[/math] of its domain, then its imaginary part will be: [math]\displaystyle{ I(x, y) ~=~ \begin{cases} ~R({\color{red}i} x, y) & \qquad \text{ if antilinear in the } {\color{red}1} \text{st argument} \\ ~R(x, {\color{blue}i} y) & \qquad \text{ if antilinear in the } {\color{blue}2} \text{nd argument} \\ \end{cases} }[/math] where the scalar [math]\displaystyle{ i }[/math] is always located in the same argument that the inner product is antilinear in.
Using [math]\displaystyle{ R(ix, y) = - R(x, iy), }[/math] the above formula for the imaginary part becomes: [math]\displaystyle{ I(x, y) ~=~ \begin{cases} -R(x, {\color{black}i} y) & \qquad \text{ if antilinear in the } {\color{black}1} \text{st argument} \\ -R({\color{black}i} x, y) & \qquad \text{ if antilinear in the } {\color{black}2} \text{nd argument} \\ \end{cases} }[/math]
Reconstructing the inner product
In a normed space [math]\displaystyle{ (H, \|\cdot\|), }[/math] if the parallelogram law [math]\displaystyle{ \|x+y\|^2 ~+~ \|x-y\|^2 ~=~ 2\|x\|^2+2\|y\|^2 }[/math] holds, then there exists a unique inner product [math]\displaystyle{ \langle \cdot,\ \cdot\rangle }[/math] on [math]\displaystyle{ H }[/math] such that [math]\displaystyle{ \|x\|^2 = \langle x,\ x\rangle }[/math] for all [math]\displaystyle{ x \in H. }[/math][4][1]
We will only give the real case here; the proof for complex vector spaces is analogous.
By the above formulas, if the norm is described by an inner product (as we hope), then it must satisfy [math]\displaystyle{ \langle x, \ y \rangle = \frac{1}{4} \left(\|x+y\|^2 - \|x-y\|^2\right) \quad \text{ for all } x, y \in H, }[/math]
which may serve as a definition of the unique candidate [math]\displaystyle{ \langle \cdot, \cdot \rangle }[/math] for the role of a suitable inner product. Thus, the uniqueness is guaranteed.
It remains to prove that this formula indeed defines an inner product and that this inner product induces the norm [math]\displaystyle{ \|\cdot\|. }[/math] Explicitly, the following will be shown:
- [math]\displaystyle{ \langle x, x \rangle = \|x\|^2, \quad x \in H }[/math]
- [math]\displaystyle{ \langle x, y \rangle = \langle y, x \rangle, \quad x, y \in H }[/math]
- [math]\displaystyle{ \langle x+z, y\rangle = \langle x, y\rangle + \langle z, y\rangle \quad \text{ for all } x, y, z \in H, }[/math]
- [math]\displaystyle{ \langle \alpha x, y \rangle = \alpha\langle x, y \rangle \quad \text{ for all } x, y \in H \text{ and all } \alpha \in \R }[/math]
(This axiomatization omits positivity, which is implied by (1) and the fact that [math]\displaystyle{ \|\cdot\| }[/math] is a norm.)
For properties (1) and (2), substitute: [math]\displaystyle{ \langle x, x \rangle = \frac{1}{4} \left(\|x+x\|^2 - \|x-x\|^2\right) = \|x\|^2, }[/math] and [math]\displaystyle{ \|x-y\|^2 = \|y-x\|^2. }[/math]
For property (3), it is convenient to work in reverse. It remains to show that [math]\displaystyle{ \|x+z+y\|^2 - \|x+z-y\|^2 \overset{?}{=} \|x+y\|^2 - \|x-y\|^2 + \|z+y\|^2 - \|z-y\|^2 }[/math] or equivalently, [math]\displaystyle{ 2\left(\|x+z+y\|^2 + \|x-y\|^2\right) - 2\left(\|x+z-y\|^2 + \|x+y\|^2\right) \overset{?}{=} 2\|z+y\|^2 - 2\|z-y\|^2. }[/math]
Now apply the parallelogram identity: [math]\displaystyle{ 2\|x+z+y\|^2 + 2\|x-y\|^2 = \|2x+z\|^2 + \|2y+z\|^2 }[/math] [math]\displaystyle{ 2\|x+z-y\|^2 + 2\|x+y\|^2 = \|2x+z\|^2 + \|z-2y\|^2 }[/math] Thus it remains to verify: [math]\displaystyle{ \cancel{\|2x+z\|^2} + \|2y+z\|^2 - (\cancel{\|2x+z\|^2} + \|z-2y\|^2) \overset{?}{{}={}} 2\|z+y\|^2 - 2\|z-y\|^2 }[/math] [math]\displaystyle{ \|2y+z\|^2 - \|z-2y\|^2 \overset{?}{=} 2\|z+y\|^2 - 2\|z-y\|^2 }[/math]
But the latter claim can be verified by subtracting the following two further applications of the parallelogram identity: [math]\displaystyle{ \|2y+z\|^2 + \|z\|^2 = 2\|z+y\|^2 + 2\|y\|^2 }[/math] [math]\displaystyle{ \|z-2y\|^2 + \|z\|^2 = 2\|z-y\|^2 + 2\|y\|^2 }[/math]
Thus (3) holds.
It can be verified by induction that (3) implies (4), as long as [math]\displaystyle{ \alpha \in \Z. }[/math] But "(4) when [math]\displaystyle{ \alpha \in \Z }[/math]" implies "(4) when [math]\displaystyle{ \alpha \in \Q }[/math]". And any positive-definite, real-valued, [math]\displaystyle{ \Q }[/math]-bilinear form satisfies the Cauchy–Schwarz inequality, so that [math]\displaystyle{ \langle \sdot,\sdot \rangle }[/math] is continuous. Thus [math]\displaystyle{ \langle \sdot,\sdot \rangle }[/math] must be [math]\displaystyle{ \R }[/math]-linear as well.
Another necessary and sufficient condition for there to exist an inner product that induces a given norm [math]\displaystyle{ \|\cdot\| }[/math] is for the norm to satisfy Ptolemy's inequality, which is:[6] [math]\displaystyle{ \|x - y\| \, \|z\| ~+~ \|y - z\| \, \|x\| ~\geq~ \|x - z\| \, \|y\| \qquad \text{ for all vectors } x, y, z. }[/math]
Applications and consequences
If [math]\displaystyle{ H }[/math] is a complex Hilbert space then [math]\displaystyle{ \langle x \mid y \rangle }[/math] is real if and only if its imaginary part is [math]\displaystyle{ 0 = R(x, iy) = \frac{1}{4} \left(\|x+iy\|^2 - \|x-iy\|^2\right), }[/math] which happens if and only if [math]\displaystyle{ \|x+iy\| = \|x-iy\|. }[/math] Similarly, [math]\displaystyle{ \langle x \mid y \rangle }[/math] is (purely) imaginary if and only if [math]\displaystyle{ \|x+y\| = \|x-y\|. }[/math] For example, from [math]\displaystyle{ \|x+ix\| = |1+i| \|x\| = \sqrt{2} \|x\| = |1-i| \|x\| = \|x-ix\| }[/math] it can be concluded that [math]\displaystyle{ \langle x | x \rangle }[/math] is real and that [math]\displaystyle{ \langle x | ix \rangle }[/math] is purely imaginary.
Isometries
If [math]\displaystyle{ A : H \to Z }[/math] is a linear isometry between two Hilbert spaces (so [math]\displaystyle{ \|A h\| = \|h\| }[/math] for all [math]\displaystyle{ h \in H }[/math]) then [math]\displaystyle{ \langle A h, A k \rangle_Z = \langle h, k \rangle_H \quad \text{ for all } h, k \in H; }[/math] that is, linear isometries preserve inner products.
If [math]\displaystyle{ A : H \to Z }[/math] is instead an antilinear isometry then [math]\displaystyle{ \langle A h, A k \rangle_Z = \overline{\langle h, k \rangle_H} = \langle k, h \rangle_H \quad \text{ for all } h, k \in H. }[/math]
Relation to the law of cosines
The second form of the polarization identity can be written as [math]\displaystyle{ \|\textbf{u}-\textbf{v}\|^2 = \|\textbf{u}\|^2 + \|\textbf{v}\|^2 - 2(\textbf{u} \cdot \textbf{v}). }[/math]
This is essentially a vector form of the law of cosines for the triangle formed by the vectors [math]\displaystyle{ \textbf{u}, \textbf{v}, }[/math] and [math]\displaystyle{ \textbf{u}-\textbf{v}. }[/math] In particular, [math]\displaystyle{ \textbf{u}\cdot\textbf{v} = \|\textbf{u}\|\,\|\textbf{v}\| \cos\theta, }[/math] where [math]\displaystyle{ \theta }[/math] is the angle between the vectors [math]\displaystyle{ \textbf{u} }[/math] and [math]\displaystyle{ \textbf{v}. }[/math]
The equation is numerically unstable if u and v are similar because of catastrophic cancellation and should be avoided for numeric computation.
Derivation
The basic relation between the norm and the dot product is given by the equation [math]\displaystyle{ \|\textbf{v}\|^2 = \textbf{v} \cdot \textbf{v}. }[/math]
Then [math]\displaystyle{ \begin{align} \|\textbf{u} + \textbf{v}\|^2 &= (\textbf{u} + \textbf{v}) \cdot (\textbf{u} + \textbf{v}) \\[3pt] &= (\textbf{u} \cdot \textbf{u}) + (\textbf{u} \cdot \textbf{v}) + (\textbf{v} \cdot \textbf{u}) + (\textbf{v} \cdot \textbf{v}) \\[3pt] &= \|\textbf{u}\|^2 + \|\textbf{v}\|^2 + 2(\textbf{u} \cdot \textbf{v}), \end{align} }[/math] and similarly [math]\displaystyle{ \|\textbf{u} - \textbf{v}\|^2 = \|\textbf{u}\|^2 + \|\textbf{v}\|^2 - 2(\textbf{u} \cdot \textbf{v}). }[/math]
Forms (1) and (2) of the polarization identity now follow by solving these equations for [math]\displaystyle{ \textbf{u} \cdot \textbf{v}, }[/math] while form (3) follows from subtracting these two equations. (Adding these two equations together gives the parallelogram law.)
Generalizations
Symmetric bilinear forms
The polarization identities are not restricted to inner products. If [math]\displaystyle{ B }[/math] is any symmetric bilinear form on a vector space, and [math]\displaystyle{ Q }[/math] is the quadratic form defined by [math]\displaystyle{ Q(v) = B(v, v), }[/math] then [math]\displaystyle{ \begin{align} 2 B(u, v) &= Q(u + v) - Q(u) - Q(v), \\ 2 B(u, v) &= Q(u) + Q(v) - Q(u - v), \\ 4 B(u, v) &= Q(u + v) - Q(u - v). \end{align} }[/math]
The so-called symmetrization map generalizes the latter formula, replacing [math]\displaystyle{ Q }[/math] by a homogeneous polynomial of degree [math]\displaystyle{ k }[/math] defined by [math]\displaystyle{ Q(v) = B(v, \ldots, v), }[/math] where [math]\displaystyle{ B }[/math] is a symmetric [math]\displaystyle{ k }[/math]-linear map.[7]
The formulas above even apply in the case where the field of scalars has characteristic two, though the left-hand sides are all zero in this case. Consequently, in characteristic two there is no formula for a symmetric bilinear form in terms of a quadratic form, and they are in fact distinct notions, a fact which has important consequences in L-theory; for brevity, in this context "symmetric bilinear forms" are often referred to as "symmetric forms".
These formulas also apply to bilinear forms on modules over a commutative ring, though again one can only solve for [math]\displaystyle{ B(u, v) }[/math] if 2 is invertible in the ring, and otherwise these are distinct notions. For example, over the integers, one distinguishes integral quadratic forms from integral symmetric forms, which are a narrower notion.
More generally, in the presence of a ring involution or where 2 is not invertible, one distinguishes [math]\displaystyle{ \varepsilon }[/math]-quadratic forms and [math]\displaystyle{ \varepsilon }[/math]-symmetric forms; a symmetric form defines a quadratic form, and the polarization identity (without a factor of 2) from a quadratic form to a symmetric form is called the "symmetrization map", and is not in general an isomorphism. This has historically been a subtle distinction: over the integers it was not until the 1950s that relation between "twos out" (integral quadratic form) and "twos in" (integral symmetric form) was understood – see discussion at integral quadratic form; and in the algebraization of surgery theory, Mishchenko originally used symmetric L-groups, rather than the correct quadratic L-groups (as in Wall and Ranicki) – see discussion at L-theory.
Homogeneous polynomials of higher degree
Finally, in any of these contexts these identities may be extended to homogeneous polynomials (that is, algebraic forms) of arbitrary degree, where it is known as the polarization formula, and is reviewed in greater detail in the article on the polarization of an algebraic form.
See also
- Inner product space – Generalization of the dot product; used to define Hilbert spaces
- Law of cosines – Property of all triangles on a Euclidean plane
- Mazur–Ulam theorem
- Minkowski distance – Mathematical metric in normed vector space
- Parallelogram law – The sum of the squares of the 4 sides of a parallelogram equals that of the 2 diagonals
- Ptolemy's inequality
Notes and references
- ↑ 1.0 1.1 Lax 2002, p. 53.
- ↑ Philippe Blanchard, Erwin Brüning (2003). "Proposition 14.1.2 (Fréchet–von Neumann–Jordan)". Mathematical methods in physics: distributions, Hilbert space operators, and variational methods. Birkhäuser. p. 192. ISBN 0817642285. https://books.google.com/books?id=1g2rikccHcgC&pg=PA192.
- ↑ Gerald Teschl (2009). "Theorem 0.19 (Jordan–von Neumann)". Mathematical methods in quantum mechanics: with applications to Schrödinger operators. American Mathematical Society Bookstore. p. 19. ISBN 978-0-8218-4660-5. https://www.mat.univie.ac.at/~gerald/ftp/book-schroe/.
- ↑ 4.0 4.1 4.2 4.3 Schechter 1996, pp. 601-603.
- ↑ Butler, Jon (20 June 2013). "norm - Derivation of the polarization identities?". https://math.stackexchange.com/questions/425173/derivation-of-the-polarization-identities. See Harald Hanche-Olson's answer.
- ↑ Apostol, Tom M. (1967). "Ptolemy's Inequality and the Chordal Metric" (in en). Mathematics Magazine 40 (5): 233–235. doi:10.2307/2688275. https://www.tandfonline.com/doi/pdf/10.1080/0025570X.1967.11975804.
- ↑ Butler 2013. See Keith Conrad (KCd)'s answer.
Bibliography
- Template:Lax Functional Analysis
- Rudin, Walter (January 1, 1991). Functional Analysis. International Series in Pure and Applied Mathematics. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277. https://archive.org/details/functionalanalys00rudi.
- Schechter, Eric (1996). Handbook of Analysis and Its Foundations. San Diego, CA: Academic Press. ISBN 978-0-12-622760-4. OCLC 175294365.
 |