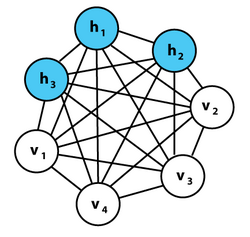
Boltzmann machine

Short description: Type of stochastic recurrent neural network

A graphical representation of an example Boltzmann machine. Each undirected edge represents dependency. In this example there are 3 hidden units and 4 visible units. This is not a restricted Boltzmann machine.

A Boltzmann machine (also called Sherrington–Kirkpatrick model with external field or stochastic Ising–Lenz–Little model) is a stochastic spin-glass model with an external field, i.e., a Sherrington–Kirkpatrick model, that is a stochastic Ising Model. It is a statistical physics technique applied in the context of cognitive science. It is also classified as Markov random field.

Boltzmann machines are theoretically intriguing because of the locality and Hebbian nature of their training algorithm (being trained by Hebb's rule), and because of their parallelism and the resemblance of their dynamics to simple physical processes. Boltzmann machines with unconstrained connectivity have not been proven useful for practical problems in machine learning or inference, but if the connectivity is properly constrained, the learning can be made efficient enough to be useful for practical problems.

They are named after the Boltzmann distribution in statistical mechanics, which is used in their sampling function. They were heavily popularized and promoted by Geoffrey Hinton, Terry Sejnowski and Yann LeCun in cognitive sciences communities and in machine learning. As a more general class within machine learning these models are called "energy based models" (EBM), because Hamiltonian of spin glasses are used as a starting point to define the learning task.

Structure

A graphical representation of a Boltzmann machine with a few weights labeled. Each undirected edge represents dependency and is weighted with weight [math]\displaystyle{ w_{ij} }[/math]. In this example there are 3 hidden units (blue) and 4 visible units (white). This is not a restricted Boltzmann machine.

A Boltzmann machine, like a Sherrington–Kirkpatrick model , is a network of units with a total "energy" (Hamiltonian) defined for the overall network. Its units produce binary results. Boltzmann machine weights are stochastic. The global energy [math]\displaystyle{ E }[/math] in a Boltzmann machine is identical in form to that of Hopfield networks and Ising models:

[math]\displaystyle{ E = -\left(\sum_{i\lt j} w_{ij} \, s_i \, s_j + \sum_i \theta_i \, s_i \right) }[/math]

Where:

• [math]\displaystyle{ w_{ij} }[/math] is the connection strength between unit [math]\displaystyle{ j }[/math] and unit [math]\displaystyle{ i }[/math].
• [math]\displaystyle{ s_i }[/math] is the state, [math]\displaystyle{ s_i \in \{0,1\} }[/math], of unit [math]\displaystyle{ i }[/math].
• [math]\displaystyle{ \theta_i }[/math] is the bias of unit [math]\displaystyle{ i }[/math] in the global energy function. ([math]\displaystyle{ -\theta_i }[/math] is the activation threshold for the unit.)

Often the weights [math]\displaystyle{ w_{ij} }[/math] are represented as a symmetric matrix [math]\displaystyle{ W=[w_{ij}] }[/math] with zeros along the diagonal.

Unit state probability

The difference in the global energy that results from a single unit [math]\displaystyle{ i }[/math] equaling 0 (off) versus 1 (on), written [math]\displaystyle{ \Delta E_i }[/math], assuming a symmetric matrix of weights, is given by:

[math]\displaystyle{ \Delta E_i = \sum_{j\gt i} w_{ij} \, s_j + \sum_{j\lt i} w_{ji} \, s_j + \theta_i }[/math]

This can be expressed as the difference of energies of two states:

[math]\displaystyle{ \Delta E_i = E_\text{i=off} - E_\text{i=on} }[/math]

Substituting the energy of each state with its relative probability according to the Boltzmann factor (the property of a Boltzmann distribution that the energy of a state is proportional to the negative log probability of that state) gives:

[math]\displaystyle{ \Delta E_i = -k_B\,T\ln(p_\text{i=off}) - (-k_B\,T\ln(p_\text{i=on})) }[/math]

where [math]\displaystyle{ k_B }[/math] is the Boltzmann constant and is absorbed into the artificial notion of temperature [math]\displaystyle{ T }[/math]. We then rearrange terms and consider that the probabilities of the unit being on and off must sum to one:

[math]\displaystyle{ \frac{\Delta E_i}{T} = \ln(p_\text{i=on}) - \ln(p_\text{i=off}) }[/math]

[math]\displaystyle{ \frac{\Delta E_i}{T} = \ln(p_\text{i=on}) - \ln(1 - p_\text{i=on}) }[/math]

[math]\displaystyle{ \frac{\Delta E_i}{T} = \ln\left(\frac{p_\text{i=on}}{1 - p_\text{i=on}}\right) }[/math]

[math]\displaystyle{ -\frac{\Delta E_i}{T} = \ln\left(\frac{1 - p_\text{i=on}}{p_\text{i=on}}\right) }[/math]

[math]\displaystyle{ -\frac{\Delta E_i}{T} = \ln\left(\frac{1}{p_\text{i=on}} - 1\right) }[/math]

[math]\displaystyle{ \exp\left(-\frac{\Delta E_i}{T}\right) = \frac{1}{p_\text{i=on}} - 1 }[/math]

Solving for [math]\displaystyle{ p_\text{i=on} }[/math], the probability that the [math]\displaystyle{ i }[/math]-th unit is on gives:

[math]\displaystyle{ p_\text{i=on} = \frac{1}{1+\exp(-\frac{\Delta E_i}{T})} }[/math]

where the scalar [math]\displaystyle{ T }[/math] is referred to as the temperature of the system. This relation is the source of the logistic function found in probability expressions in variants of the Boltzmann machine.

Equilibrium state

The network runs by repeatedly choosing a unit and resetting its state. After running for long enough at a certain temperature, the probability of a global state of the network depends only upon that global state's energy, according to a Boltzmann distribution, and not on the initial state from which the process was started. This means that log-probabilities of global states become linear in their energies. This relationship is true when the machine is "at thermal equilibrium", meaning that the probability distribution of global states has converged. Running the network beginning from a high temperature, its temperature gradually decreases until reaching a thermal equilibrium at a lower temperature. It then may converge to a distribution where the energy level fluctuates around the global minimum. This process is called simulated annealing.

To train the network so that the chance it will converge to a global state according to an external distribution over these states, the weights must be set so that the global states with the highest probabilities get the lowest energies. This is done by training.

Training

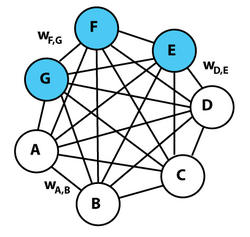
The units in the Boltzmann machine are divided into 'visible' units, V, and 'hidden' units, H. The visible units are those that receive information from the 'environment', i.e. the training set is a set of binary vectors over the set V. The distribution over the training set is denoted [math]\displaystyle{ P^{+}(V) }[/math].

The distribution over global states converges as the Boltzmann machine reaches thermal equilibrium. We denote this distribution, after we marginalize it over the hidden units, as [math]\displaystyle{ P^{-}(V) }[/math].

Our goal is to approximate the "real" distribution [math]\displaystyle{ P^{+}(V) }[/math] using the [math]\displaystyle{ P^{-}(V) }[/math] produced by the machine. The similarity of the two distributions is measured by the Kullback–Leibler divergence, [math]\displaystyle{ G }[/math]:

[math]\displaystyle{ G = \sum_{v}{P^{+}(v)\ln\left({\frac{P^{+}(v)}{P^{-}(v)}}\right)} }[/math]

where the sum is over all the possible states of [math]\displaystyle{ V }[/math]. [math]\displaystyle{ G }[/math] is a function of the weights, since they determine the energy of a state, and the energy determines [math]\displaystyle{ P^{-}(v) }[/math], as promised by the Boltzmann distribution. A gradient descent algorithm over [math]\displaystyle{ G }[/math], changes a given weight, [math]\displaystyle{ w_{ij} }[/math] by subtracting the partial derivative of [math]\displaystyle{ G }[/math] with respect to the weight.

Boltzmann machine training involves two alternating phases. One is the "positive" phase where the visible units' states are clamped to a particular binary state vector sampled from the training set (according to [math]\displaystyle{ P^{+} }[/math]). The other is the "negative" phase where the network is allowed to run freely, i.e. only the input nodes have their state determined by external data, but the output nodes are allowed to float. The gradient with respect to a given weight, [math]\displaystyle{ w_{ij} }[/math], is given by the equation:

[math]\displaystyle{ \frac{\partial{G}}{\partial{w_{ij}}} = -\frac{1}{R}[p_{ij}^{+}-p_{ij}^{-}] }[/math]

where:

• [math]\displaystyle{ p_{ij}^{+} }[/math] is the probability that units i and j are both on when the machine is at equilibrium on the positive phase.
• [math]\displaystyle{ p_{ij}^{-} }[/math] is the probability that units i and j are both on when the machine is at equilibrium on the negative phase.
• [math]\displaystyle{ R }[/math] denotes the learning rate

This result follows from the fact that at thermal equilibrium the probability [math]\displaystyle{ P^{-}(s) }[/math] of any global state [math]\displaystyle{ s }[/math] when the network is free-running is given by the Boltzmann distribution.

This learning rule is biologically plausible because the only information needed to change the weights is provided by "local" information. That is, the connection (synapse, biologically) does not need information about anything other than the two neurons it connects. This is more biologically realistic than the information needed by a connection in many other neural network training algorithms, such as backpropagation.

The training of a Boltzmann machine does not use the EM algorithm, which is heavily used in machine learning. By minimizing the KL-divergence, it is equivalent to maximizing the log-likelihood of the data. Therefore, the training procedure performs gradient ascent on the log-likelihood of the observed data. This is in contrast to the EM algorithm, where the posterior distribution of the hidden nodes must be calculated before the maximization of the expected value of the complete data likelihood during the M-step.

Training the biases is similar, but uses only single node activity:

[math]\displaystyle{ \frac{\partial{G}}{\partial{\theta_{i}}} = -\frac{1}{R}[p_{i}^{+}-p_{i}^{-}] }[/math]

Problems

Theoretically the Boltzmann machine is a rather general computational medium. For instance, if trained on photographs, the machine would theoretically model the distribution of photographs, and could use that model to, for example, complete a partial photograph.

Unfortunately, Boltzmann machines experience a serious practical problem, namely that it seems to stop learning correctly when the machine is scaled up to anything larger than a trivial size. This is due to important effects, specifically:

• the required time order to collect equilibrium statistics grows exponentially with the machine's size, and with the magnitude of the connection strengths
• connection strengths are more plastic when the connected units have activation probabilities intermediate between zero and one, leading to a so-called variance trap. The net effect is that noise causes the connection strengths to follow a random walk until the activities saturate.

Types

Restricted Boltzmann machine

Graphical representation of a restricted Boltzmann machine. The four blue units represent hidden units, and the three red units represent visible states. In restricted Boltzmann machines there are only connections (dependencies) between hidden and visible units, and none between units of the same type (no hidden-hidden, nor visible-visible connections).

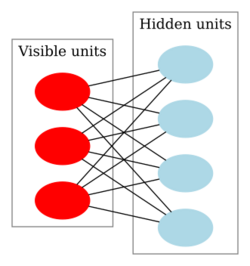
Although learning is impractical in general Boltzmann machines, it can be made quite efficient in a restricted Boltzmann machine (RBM) which does not allow intralayer connections between hidden units and visible units, i.e. there is no connection between visible to visible and hidden to hidden units. After training one RBM, the activities of its hidden units can be treated as data for training a higher-level RBM. This method of stacking RBMs makes it possible to train many layers of hidden units efficiently and is one of the most common deep learning strategies. As each new layer is added the generative model improves.

An extension to the restricted Boltzmann machine allows using real valued data rather than binary data.

One example of a practical RBM application is in speech recognition.

Deep Boltzmann machine

A deep Boltzmann machine (DBM) is a type of binary pairwise Markov random field (undirected probabilistic graphical model) with multiple layers of hidden random variables. It is a network of symmetrically coupled stochastic binary units. It comprises a set of visible units [math]\displaystyle{ \boldsymbol{\nu} \in \{0,1\}^D }[/math] and layers of hidden units [math]\displaystyle{ \boldsymbol{h}^{(1)} \in \{0,1\}^{F_1}, \boldsymbol{h}^{(2)} \in \{0,1\}^{F_2}, \ldots, \boldsymbol{h}^{(L)} \in \{0,1\}^{F_L} }[/math]. No connection links units of the same layer (like RBM). For the DBM, the probability assigned to vector ν is

[math]\displaystyle{ p(\boldsymbol{\nu}) = \frac{1}{Z}\sum_h e^{\sum_{ij}W_{ij}^{(1)}\nu_i h_j^{(1)} + \sum_{jl}W_{jl}^{(2)}h_j^{(1)}h_l^{(2)}+\sum_{lm}W_{lm}^{(3)}h_l^{(2)}h_m^{(3)}}, }[/math]

where [math]\displaystyle{ \boldsymbol{h} = \{\boldsymbol{h}^{(1)}, \boldsymbol{h}^{(2)}, \boldsymbol{h}^{(3)} \} }[/math] are the set of hidden units, and [math]\displaystyle{ \theta = \{\boldsymbol{W}^{(1)}, \boldsymbol{W}^{(2)}, \boldsymbol{W}^{(3)} \} }[/math] are the model parameters, representing visible-visible, visible-hidden and hidden-hidden interactions. In a DBN only the top two layers form a restricted Boltzmann machine (which is an undirected graphical model), while lower layers form a directed generative model. In a DBM all layers are symmetric and undirected.

Like DBNs, DBMs can learn complex and abstract internal representations of the input in tasks such as object or speech recognition, using limited, labeled data to fine-tune the representations built using a large set of unlabeled sensory input data. However, unlike DBNs and deep convolutional neural networks, they pursue the inference and training procedure in both directions, bottom-up and top-down, which allow the DBM to better unveil the representations of the input structures.

However, the slow speed of DBMs limits their performance and functionality. Because exact maximum likelihood learning is intractable for DBMs, only approximate maximum likelihood learning is possible. Another option is to use mean-field inference to estimate data-dependent expectations and approximate the expected sufficient statistics by using Markov chain Monte Carlo (MCMC). This approximate inference, which must be done for each test input, is about 25 to 50 times slower than a single bottom-up pass in DBMs. This makes joint optimization impractical for large data sets, and restricts the use of DBMs for tasks such as feature representation.

Spike-and-slab RBMs

The need for deep learning with real-valued inputs, as in Gaussian RBMs, led to the spike-and-slab RBM (ssRBM), which models continuous-valued inputs with binary latent variables. Similar to basic RBMs and its variants, a spike-and-slab RBM is a bipartite graph, while like GRBMs, the visible units (input) are real-valued. The difference is in the hidden layer, where each hidden unit has a binary spike variable and a real-valued slab variable. A spike is a discrete probability mass at zero, while a slab is a density over continuous domain; their mixture forms a prior.

An extension of ssRBM called µ-ssRBM provides extra modeling capacity using additional terms in the energy function. One of these terms enables the model to form a conditional distribution of the spike variables by marginalizing out the slab variables given an observation.

In Mathematics

Main articles: Gibbs measure and Log-linear model

In more general mathematical setting, the Boltzmann distribution is also known as the Gibbs measure. In statistics and machine learning it is called a log-linear model. In deep learning the Boltzmann distribution is used in the sampling distribution of stochastic neural networks such as the Boltzmann machine.

History

The Boltzmann machine is based on a spin-glass model of Sherrington-Kirkpatrick's stochastic Ising Model.

The original contribution in applying such energy based models in cognitive science appeared in papers by Hinton and Sejnowski.

The seminal publication by John Hopfield connected physics and statistical mechanics, mentioning spin glasses.

The idea of applying the Ising model with annealed Gibbs sampling is present in Douglas Hofstadter's Copycat project.

Similar ideas (with a change of sign in the energy function) are found in Paul Smolensky's "Harmony Theory".

The explicit analogy drawn with statistical mechanics in the Boltzmann Machine formulation led to the use of terminology borrowed from physics (e.g., "energy" rather than "harmony"), which became standard in the field. The widespread adoption of this terminology may have been encouraged by the fact that its use led to the adoption of a variety of concepts and methods from statistical mechanics. The various proposals to use simulated annealing for inference were apparently independent.

Ising models became considered to be a special case of Markov random fields, which find widespread application in linguistics, robotics, computer vision and artificial intelligence.

See also

• Restricted Boltzmann machine
• Helmholtz machine
• Markov Random Field
• Ising Model
• Hopfield network
• Learning rule that uses conditional "local" information can be derived from the reversed form of [math]\displaystyle{ G }[/math],

[math]\displaystyle{ G' = \sum_{v}{P^{-}(v)\ln\left({\frac{P^{-}(v)}{P^{+}(v)}}\right)} }[/math].

References

1. https://www.mis.mpg.de/preprints/2018/preprint2018_87.pdf

Further reading

• Hinton, G. E.; Sejnowski, T. J. (1986). D. E. Rumelhart. ed. "Learning and Relearning in Boltzmann Machines". Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Volume 1: Foundations: 282–317. http://www.cs.toronto.edu/~hinton/absps/pdp7.pdf. 
• "Training Products of Experts by Minimizing Contrastive Divergence". Neural Computation 14 (8): 1771–1800. 2002. doi:10.1162/089976602760128018. PMID 12180402. http://www.cs.toronto.edu/~hinton/absps/nccd.pdf. 
• "A fast learning algorithm for deep belief nets". Neural Computation 18 (7): 1527–1554. 2006. doi:10.1162/neco.2006.18.7.1527. PMID 16764513. http://www.cs.toronto.edu/~hinton/absps/fastnc.pdf. 

External links

• Scholarpedia article by Hinton about Boltzmann machines
• Talk at Google by Geoffrey Hinton