Astronomy:Multistage rocket


A multistage rocket or step rocket[1] is a launch vehicle that uses two or more rocket stages, each of which contains its own engines and propellant. A tandem or serial stage is mounted on top of another stage; a parallel stage is attached alongside another stage. The result is effectively two or more rockets stacked on top of or attached next to each other. Two-stage rockets are quite common, but rockets with as many as five separate stages have been successfully launched.
By jettisoning stages when they run out of propellant, the mass of the remaining rocket is decreased. Each successive stage can also be optimized for its specific operating conditions, such as decreased atmospheric pressure at higher altitudes. This staging allows the thrust of the remaining stages to more easily accelerate the rocket to its final speed and height.
In serial or tandem staging schemes, the first stage is at the bottom and is usually the largest, the second stage and subsequent upper stages are above it, usually decreasing in size. In parallel staging schemes solid or liquid rocket boosters are used to assist with launch. These are sometimes referred to as "stage 0". In the typical case, the first-stage and booster engines fire to propel the entire rocket upwards. When the boosters run out of fuel, they are detached from the rest of the rocket (usually with some kind of small explosive charge or explosive bolts) and fall away. The first stage then burns to completion and falls off. This leaves a smaller rocket, with the second stage on the bottom, which then fires. Known in rocketry circles as staging, this process is repeated until the desired final velocity is achieved. In some cases with serial staging, the upper stage ignites before the separation—the interstage ring is designed with this in mind, and the thrust is used to help positively separate the two vehicles.
A multistage rocket is required to reach orbital speed. Single-stage-to-orbit designs are sought, but have not yet been demonstrated.
Performance



The reason multi-stage rockets are required is the limitation the laws of physics place on the maximum velocity achievable by a rocket of given fueled-to-dry mass ratio. This relation is given by the classical rocket equation:
where:
- is delta-v of the vehicle (change of velocity plus losses due to gravity and atmospheric drag);
- is the initial total (wet) mass, equal to final (dry) mass plus propellant;
- is the final (dry) mass, after the propellant is expended;
- is the effective exhaust velocity (determined by propellant, engine design and throttle condition);
- is the natural logarithm function.
The delta v required to reach low Earth orbit (or the required velocity of a sufficiently heavy suborbital payload) requires a wet to dry mass ratio larger than can realistically be achieved in a single rocket stage. The multistage rocket overcomes this limit by splitting the delta-v into fractions. As each lower stage drops off and the succeeding stage fires, the rest of the rocket is still traveling near the burnout speed. Each lower stage's dry mass includes the propellant in the upper stages, and each succeeding upper stage has reduced its dry mass by discarding the useless dry mass of the spent lower stages.[2]
A further advantage is that each stage can use a different type of rocket engine, each tuned for its particular operating conditions. Thus the lower-stage engines are designed for use at atmospheric pressure, while the upper stages can use engines suited to near vacuum conditions. Lower stages tend to require more structure than upper as they need to bear their own weight plus that of the stages above them. Optimizing the structure of each stage decreases the weight of the total vehicle and provides further advantage.
The advantage of staging comes at the cost of the lower stages lifting engines which are not yet being used, as well as making the entire rocket more complex and harder to build than a single stage. In addition, each staging event is a possible point of launch failure, due to separation failure, ignition failure, or stage collision. Nevertheless, the savings are so great that every rocket ever used to deliver a payload into orbit has had staging of some sort.
One of the most common measures of rocket efficiency is its specific impulse, which is defined as the thrust per flow rate (per second) of propellant consumption:[3]
- =
When rearranging the equation such that thrust is calculated as a result of the other factors, we have:
These equations show that a higher specific impulse means a more efficient rocket engine, capable of burning for longer periods of time. In terms of staging, the initial rocket stages usually have a lower specific impulse rating, trading efficiency for superior thrust in order to quickly push the rocket into higher altitudes. Later stages of the rocket usually have a higher specific impulse rating because the vehicle is further outside the atmosphere and the exhaust gas does not need to expand against as much atmospheric pressure.
When selecting the ideal rocket engine to use as an initial stage for a launch vehicle, a useful performance metric to examine is the thrust-to-weight ratio, and is calculated by the equation:
The common thrust-to-weight ratio of a launch vehicle is within the range of 1.3 to 2.0.[3] Another performance metric to keep in mind when designing each rocket stage in a mission is the burn time, which is the amount of time the rocket engine will last before it has exhausted all of its propellant. For most non-final stages, thrust and specific impulse can be assumed constant, which allows the equation for burn time to be written as:
Where and are the initial and final masses of the rocket stage respectively. In conjunction with the burnout time, the burnout height and velocity are obtained using the same values, and are found by these two equations:
When dealing with the problem of calculating the total burnout velocity or time for the entire rocket system, the general procedure for doing so is as follows:[3]
- Partition the problem calculations into however many stages the rocket system comprises.
- Calculate the initial and final mass for each individual stage.
- Calculate the burnout velocity, and sum it with the initial velocity for each individual stage. Assuming each stage occurs immediately after the previous, the burnout velocity becomes the initial velocity for the following stage.
- Repeat the previous two steps until the burnout time and/or velocity has been calculated for the final stage.
It is important to note that the burnout time does not define the end of the rocket stage's motion, as the vehicle will still have a velocity that will allow it to coast upward for a brief amount of time until the acceleration of the planet's gravity gradually changes it to a downward direction. The velocity and altitude of the rocket after burnout can be easily modeled using the basic physics equations of motion.
When comparing one rocket with another, it is impractical to directly compare the rocket's certain trait with the same trait of another because their individual attributes are often not independent of one another. For this reason, dimensionless ratios have been designed to enable a more meaningful comparison between rockets. The first is the initial to final mass ratio, which is the ratio between the rocket stage's full initial mass and the rocket stage's final mass once all of its fuel has been consumed. The equation for this ratio is:
Where is the empty mass of the stage, is the mass of the propellant, and is the mass of the payload.[4] The second dimensionless performance quantity is the structural ratio, which is the ratio between the empty mass of the stage, and the combined empty mass and propellant mass as shown in this equation:[4]
The last major dimensionless performance quantity is the payload ratio, which is the ratio between the payload mass and the combined mass of the empty rocket stage and the propellant:
After comparing the three equations for the dimensionless quantities, it is easy to see that they are not independent of each other, and in fact, the initial to final mass ratio can be rewritten in terms of structural ratio and payload ratio:[4]
These performance ratios can also be used as references for how efficient a rocket system will be when performing optimizations and comparing varying configurations for a mission.
Component selection and sizing
For initial sizing, the rocket equations can be used to derive the amount of propellant needed for the rocket based on the specific impulse of the engine and the total impulse required in N·s. The equation is:
where g is the gravity constant of Earth.[3] This also enables the volume of storage required for the fuel to be calculated if the density of the fuel is known, which is almost always the case when designing the rocket stage. The volume is yielded when dividing the mass of the propellant by its density. Asides from the fuel required, the mass of the rocket structure itself must also be determined, which requires taking into account the mass of the required thrusters, electronics, instruments, power equipment, etc.[3] These are known quantities for typical off the shelf hardware that should be considered in the mid to late stages of the design, but for preliminary and conceptual design, a simpler approach can be taken. Assuming one engine for a rocket stage provides all of the total impulse for that particular segment, a mass fraction can be used to determine the mass of the system. The mass of the stage transfer hardware such as initiators and safe-and-arm devices are very small by comparison and can be considered negligible.
For modern day solid rocket motors, it is a safe and reasonable assumption to say that 91 to 94 percent of the total mass is fuel.[3] It is also important to note there is a small percentage of "residual" propellant that will be left stuck and unusable inside the tank, and should also be taken into consideration when determining amount of fuel for the rocket. A common initial estimate for this residual propellant is five percent. With this ratio and the mass of the propellant calculated, the mass of the empty rocket weight can be determined. Sizing rockets using a liquid bipropellant requires a slightly more involved approach because there are two separate tanks that are required: one for the fuel, and one for the oxidizer. The ratio of these two quantities is known as the mixture ratio, and is defined by the equation:
Where is the mass of the oxidizer and is the mass of the fuel. This mixture ratio not only governs the size of each tank, but also the specific impulse of the rocket. Determining the ideal mixture ratio is a balance of compromises between various aspects of the rocket being designed, and can vary depending on the type of fuel and oxidizer combination being used. For example, a mixture ratio of a bipropellant could be adjusted such that it may not have the optimal specific impulse, but will result in fuel tanks of equal size. This would yield simpler and cheaper manufacturing, packing, configuring, and integrating of the fuel systems with the rest of the rocket,[3] and can become a benefit that could outweigh the drawbacks of a less efficient specific impulse rating. But suppose the defining constraint for the launch system is volume, and a low density fuel is required such as hydrogen. This example would be solved by using an oxidizer-rich mixture ratio, reducing efficiency and specific impulse rating, but will meet a smaller tank volume requirement.
Optimal staging and restricted staging
Optimal
The ultimate goal of optimal staging is to maximize the payload ratio (see ratios under performance), meaning the largest amount of payload is carried up to the required burnout velocity using the least amount of non-payload mass, which comprises everything else. This goal assumes that the cost of a rocket launch is proportional to the total liftoff mass of the rocket, which is a rule of thumb in rocket engineering. Here are a few quick rules and guidelines to follow in order to reach optimal staging:[3]
- Initial stages should have lower , and later/final stages should have higher .
- The stages with the lower should contribute less ΔV.
- The next stage is always a smaller size than the previous stage.
- Similar stages should provide similar ΔV.
The payload ratio can be calculated for each individual stage, and when multiplied together in sequence, will yield the overall payload ratio of the entire system. It is important to note that when computing payload ratio for individual stages, the payload includes the mass of all the stages after the current one. The overall payload ratio is:
Where n is the number of stages the rocket system comprises. Similar stages yielding the same payload ratio simplify this equation, however that is seldom the ideal solution for maximizing payload ratio, and ΔV requirements may have to be partitioned unevenly as suggested in guideline tips 1 and 2 from above. Two common methods of determining this perfect ΔV partition between stages are either a technical algorithm that generates an analytical solution that can be implemented by a program, or simple trial and error.[3] For the trial and error approach, it is best to begin with the final stage, calculating the initial mass which becomes the payload for the previous stage. From there it is easy to progress all the way down to the initial stage in the same manner, sizing all the stages of the rocket system.
Restricted
Restricted rocket staging is based on the simplified assumption that each of the stages of the rocket system have the same specific impulse, structural ratio, and payload ratio, the only difference being the total mass of each increasing stage is less than that of the previous stage. Although this assumption may not be the ideal approach to yielding an efficient or optimal system, it greatly simplifies the equations for determining the burnout velocities, burnout times, burnout altitudes, and mass of each stage. This would make for a better approach to a conceptual design in a situation where a basic understanding of the system behavior is preferential to a detailed, accurate design. One important concept to understand when undergoing restricted rocket staging, is how the burnout velocity is affected by the number of stages that split up the rocket system. Increasing the number of stages for a rocket while keeping the specific impulse, payload ratios and structural ratios constant will always yield a higher burnout velocity than the same systems that use fewer stages. However, the law of diminishing returns is evident in that each increment in number of stages gives less of an improvement in burnout velocity than the previous increment. The burnout velocity gradually converges towards an asymptotic value as the number of stages increases towards a very high number.[4] In addition to diminishing returns in burnout velocity improvement, the main reason why real world rockets seldom use more than three stages is because of increase of weight and complexity in the system for each added stage, ultimately yielding a higher cost for deployment.
Hot-staging
Hot-staging is a type of rocket staging in which the next stage fires its engines before separation instead of after.[5] During hot-staging, the earlier stage throttles down its engines.[5] Hot-staging may reduce the complexity of stage separation, and gives a small extra payload capacity to the booster.[5] It also eliminates the need for ullage motors, as the acceleration from the nearly-spent stage keeps the propellants settled at the bottom of the tanks. Hot-staging is used on Soviet-era Russian rockets such as Soyuz[6][7] and Proton-M.[8] The N1 rocket was designed to use hot staging, however none of the test flights lasted long enough for this to occur. Starting with the Titan II, the Titan family of rockets used hot staging. SpaceX retrofitted their Starship rocket to use hot staging on its second flight, making it the largest rocket ever to do so.[9]
Tandem vs parallel staging design
A rocket system that implements tandem staging means that each individual stage runs in order one after the other. The rocket breaks free from the previous stage, then begins burning through the next stage in straight succession. On the other hand, a rocket that implements parallel staging has two or more different stages that are active at the same time. For example, the Space Shuttle has two Solid Rocket Boosters that burn simultaneously. Upon launch, the boosters ignite, and at the end of the stage, the two boosters are discarded while the external fuel tank is kept for another stage.[3] Most quantitative approaches to the design of the rocket system's performance are focused on tandem staging, but the approach can be easily modified to include parallel staging. To begin with, the different stages of the rocket should be clearly defined. Continuing with the previous example, the end of the first stage which is sometimes referred to as 'stage 0', can be defined as when the side boosters separate from the main rocket. From there, the final mass of stage one can be considered the sum of the empty mass of stage one, the mass of stage two (the main rocket and the remaining unburned fuel) and the mass of the payload.[original research?]
Upper stages
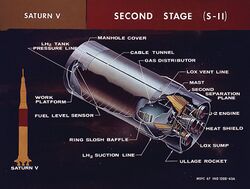
High-altitude and space-bound upper stages are designed to operate with little or no atmospheric pressure. This allows the use of lower pressure combustion chambers and engine nozzles with optimal vacuum expansion ratios. Some upper stages, especially those using hypergolic propellants like Delta-K or Ariane 5 ES second stage, are pressure fed, which eliminates the need for complex turbopumps. Other upper stages, such as the Centaur or DCSS, use liquid hydrogen expander cycle engines, or gas generator cycle engines like the Ariane 5 ECA's HM7B or the S-IVB's J-2. These stages are usually tasked with completing orbital injection and accelerating payloads into higher energy orbits such as GTO or to escape velocity. Upper stages, such as Fregat, used primarily to bring payloads from low Earth orbit to GTO or beyond are sometimes referred to as space tugs.[10]
Assembly
Each individual stage is generally assembled at its manufacturing site and shipped to the launch site; the term vehicle assembly refers to the mating of all rocket stage(s) and the spacecraft payload into a single assembly known as a space vehicle. Single-stage vehicles (suborbital), and multistage vehicles on the smaller end of the size range, can usually be assembled directly on the launch pad by lifting the stage(s) and spacecraft vertically in place by means of a crane.
This is generally not practical for larger space vehicles, which are assembled off the pad and moved into place on the launch site by various methods. NASA's Apollo/Saturn V crewed Moon landing vehicle, and Space Shuttle, were assembled vertically onto mobile launcher platforms with attached launch umbilical towers, in a Vehicle Assembly Building, and then a special crawler-transporter moved the entire vehicle stack to the launch pad in an upright position. In contrast, vehicles such as the Russian Soyuz rocket and the SpaceX Falcon 9 are assembled horizontally in a processing hangar, transported horizontally, and then brought upright at the pad.
Passivation and space debris
Johnson, Nicholas (2011-12-05). "Space debris issues". audio file, @1:03:05-1:06:20. The Space Show. http://www.thespaceshow.com/detail.asp?q=1666.</ref> Passivation means removing any sources of stored energy remaining on the vehicle, as by dumping fuel or discharging batteries.
Many early upper stages, in both the Soviet and U.S. space programs, were not passivated after mission completion. During the initial attempts to characterize the space debris problem, it became evident that a good proportion of all debris was due to the breaking up of rocket upper stages, particularly unpassivated upper-stage propulsion units.[11]
History and development
An illustration and description in the 14th century Chinese Huolongjing by Jiao Yu and Liu Bowen shows the oldest known multistage rocket; this was the "fire-dragon issuing from the water" (火龙出水, huǒ lóng chū shuǐ), which was used mostly by the Chinese navy.[12][13] It was a two-stage rocket that had booster rockets that would eventually burn out, yet before they did they automatically ignited a number of smaller rocket arrows that were shot out of the front end of the missile, which was shaped like a dragon's head with an open mouth.[13] The British scientist and historian Joseph Needham points out that the written material and depicted illustration of this rocket come from the oldest stratum of the Huolongjing, which can be dated roughly 1300–1350 AD (from the book's part 1, chapter 3, page 23).[13]
Another example of an early multistaged rocket is the Juhwa (走火) of Korean development. It was proposed by medieval Korean engineer, scientist and inventor Choe Museon and developed by the Firearms Bureau (火㷁道監) during the 14th century.[14][15] The rocket had the length of 15 cm and 13 cm; the diameter was 2.2 cm. It was attached to an arrow 110 cm long; experimental records show that the first results were around 200m in range.[16] There are records that show Korea kept developing this technology until it came to produce the Singijeon, or 'magical machine arrows' in the 16th century. The earliest experiments with multistage rockets in Europe were made in 1551 by Austrian Conrad Haas (1509–1576), the arsenal master of the town of Hermannstadt, Transylvania (now Sibiu/Hermannstadt, Romania). This concept was developed independently by at least five individuals:
- Polish–Lithuanian Kazimieras Simonavičius (1600–1651)[17][18][19]
- Russia n Konstantin Tsiolkovsky (1857–1935)
- United States Robert Goddard (1882–1945)
- German Hermann Oberth (1894–1989)
- French Louis Damblanc (fr) (1889–1969)
The first high-speed multistage rockets were the RTV-G-4 Bumper rockets tested at the White Sands Proving Ground and later at Cape Canaveral from 1948 to 1950. These consisted of a V-2 rocket and a WAC Corporal sounding rocket. The greatest altitude ever reached was 393 km, attained on February 24, 1949, at White Sands.
In 1947, the Soviet rocket engineer and scientist Mikhail Tikhonravov developed a theory of parallel stages, which he called "packet rockets". In his scheme, three parallel stages were fired from liftoff, but all three engines were fueled from the outer two stages, until they are empty and could be ejected. This is more efficient than sequential staging, because the second-stage engine is never just dead weight. In 1951, Soviet engineer and scientist Dmitry Okhotsimsky carried out a pioneering engineering study of general sequential and parallel staging, with and without the pumping of fuel between stages. The design of the R-7 Semyorka emerged from that study. The trio of rocket engines used in the first stage of the American Atlas I and Atlas II launch vehicles, arranged in a row, used parallel staging in a similar way: the outer pair of booster engines existed as a jettisonable pair which would, after they shut down, drop away with the lowermost outer skirt structure, leaving the central sustainer engine to complete the first stage's engine burn towards apogee or orbit.
Separation events
Separation of each portion of a multistage rocket introduces additional risk into the success of the launch mission. Reducing the number of separation events results in a reduction in complexity.[20] Separation events occur when stages or strap-on boosters separate after use, when the payload fairing separates prior to orbital insertion, or when used, a launch escape system which separates after the early phase of a launch. Pyrotechnic fasteners, or in some cases pneumatic systems like on the Falcon 9 Full Thrust, are typically used to separate rocket stages.
Two-stage-to-orbit
Three-stage-to-orbit
The three-stage-to-orbit launch system is a commonly used rocket system to attain Earth orbit. The spacecraft uses three distinct stages to provide propulsion consecutively in order to achieve orbital velocity. It is intermediate between a four-stage-to-orbit launcher and a two-stage-to-orbit launcher.
Examples of three-stage-to-orbit systems
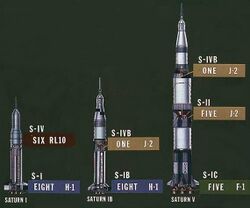
- Saturn V[21]
- Vanguard[22]
- Ariane 4 (optional boosters)
- Ariane 2
- Ariane 1 (four stages)
- GSLV (three stages and boosters)
- PSLV (four stages)
- Proton (optional fourth stage)
- Long March 5 (optional boosters and optional third stage)
- Long March 1, Long March 1D[citation needed]
- Zenit-3SL
- KSLV-2 "Nuri"[citation needed]
Examples of two stages with boosters
Other designs (in fact, most modern medium- to heavy-lift designs) do not have all three stages inline on the main stack, instead having strap-on boosters for the "stage-0" with two core stages. In these designs, the boosters and first stage fire simultaneously instead of consecutively, providing extra initial thrust to lift the full launcher weight and overcome gravity losses and atmospheric drag. The boosters are jettisoned a few minutes into flight to reduce weight.
- US Space Shuttle — SRB first stage ; External Tank + SSME second stage ; OMS on internal tanks third stage ;
- Angara A5
- Ariane 5
- Atlas V 551[23]
- Delta II third stage)
- Delta IV-Medium+ and -Heavy
- Falcon Heavy[24]
- Geosynchronous Satellite Launch Vehicle Mk III (However, like the Titan IIIC, the GSLV MkIII is launched solely by the side boosters. The main core only ignites a few minutes into flight, shortly before the boosters are jettisoned.)
- H-IIA, H-IIB[citation needed]
- Soyuz
- Space Launch System
- Titan IV
- Long March 2E, Long March 2F, Long March 3B[citation needed]
Four-stage-to-orbit
The four-stage-to-orbit launch system is a rocket system used to attain Earth orbit. The spacecraft uses four distinct stages to provide propulsion consecutively in order to achieve orbital velocity. It is intermediate between a five-stage-to-orbit launcher and a three-stage-to-orbit launcher, most often used with solid-propellant launch systems.
Examples of four-stage-to-orbit systems[citation needed]
- Ariane 1
- PSLV
- Minotaur IV
- Proton (optional fourth stage)
- Minotaur V (five stages)
- ASLV (five stages)
Examples of three stages with boosters[citation needed]
Other designs do not have all four stages inline on the main stack, instead having strap-on boosters for the "stage-0" with three core stages. In these designs, the boosters and first stage fire simultaneously instead of consecutively, providing extra initial thrust to lift the full launcher weight and overcome gravity losses and atmospheric drag. The boosters are jettisoned a few minutes into flight to reduce weight.
- Long March 5 (optional boosters and optional third stage)
Extraterrestrial Rockets
- NASA-ESA Mars Ascent Vehicle(MAV) (A 2-stage rocket, planned launch from Mars in 2028)
See also
- Multistage rocket
- Adapter
- Reusable launch system
- Space tug
- Apogee kick motor
- Conrad Haas
- Modular rocket
- Huolongchushui
References
- ↑ "Brief History of Rockets". https://www.grc.nasa.gov/www/k-12/TRC/Rockets/history_of_rockets.html.
- ↑ Blanco, Philip (2022). "Learning about rockets, in stages". Physics Education 57 (4): 045035. doi:10.1088/1361-6552/ac6928. Bibcode: 2022PhyEd..57d5035B. https://iopscience.iop.org/article/10.1088/1361-6552/ac6928. Retrieved 17 June 2022.
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 Curtis, Howard. "Rocket Vehicle Dynamics." Orbital Mechanics for Engineering Students. 2nd ed. Daytona Beach: Elsevier, 2010. Print
- ↑ 5.0 5.1 5.2 Skibba, Ramin. "Here’s What’s Next for SpaceX’s Starship" (in en-US). Wired. ISSN 1059-1028. https://www.wired.com/story/heres-whats-next-for-spacexs-starship/.
- ↑ Sesnic, Trevor (2020-02-04). "One Web 2 | Soyuz 2.1b/Fregat-M" (in en-US). https://everydayastronaut.com/soyuz-2-1b-fregat-m-oneweb-2/.
- ↑ "SpaceX Achieves New Milestones With Second Starship Flight" (in en). https://www.supercluster.com/editorial/spacex-achieves-new-milestones-with-second-starship-flight.
- ↑ "Proton-M flyout continues with launch of Angosat-2 - NASASpaceFlight.com". 2023-06-05. https://www.nasaspaceflight.com/2022/10/angosat-2/.
- ↑ "SpaceX Starship Never Stops Thrusting With Hot Staging | NextBigFuture.com" (in en-US). 2023-06-24. https://www.nextbigfuture.com/2023/06/spacex-starship-never-stop-thrusting-with-hot-staging.html.
- ↑ "Fregat". http://www.russianspaceweb.com/fregat.html.
- ↑ Loftus, Joseph P. (1989). Orbital Debris from Upper-stage Breakup. AIAA. pp. 227. ISBN 9781600863769. https://books.google.com/books?id=RehH7b_kmNEC.
- ↑ "火龙出水(明)简介". 星辰在线. 2003-12-26. http://www.csonline.com.cn/zt/ztchangsha/ht/htz_2/t20031226_84913.htm.
- ↑ 13.0 13.1 13.2 Needham, Volume 5, Part 7, 510.
- ↑ :ko:주화 (무기)
- ↑ :ko:화통도감
- ↑ "주화 (走火)". 한국민족문화대백과. 1999-09-25. http://terms.naver.com/entry.nhn?cid=1608&docId=550070&mobile&categoryId=1608.
- ↑ Ulrich Walter (2008). Astronautics. Wiley-VCH. p. 44. ISBN 978-3-527-40685-2.
- ↑ Balčiūnienė, Irma. "VIENO EKSPONATO PARODA: KNYGA "DIDYSIS ARTILERIJOS MENAS"!" (in lt-LT). Lithuanian Museum of Ethnocosmology. http://www.etnokosmomuziejus.lt/lt/vieno-eksponato-paroda-knyga-didysis-artilerijos-menas/.
- ↑ Simonaitis, Ričardas. "Lietuvos kariuomenei - 95". http://aidas.lt/lt/istorija/article/9429-11-23-lietuvos-kariuomenei-95.
- ↑ "Falcon 1 – Stage Separation Reliability". SpaceX. http://www.spacex.com/falcon1.php#engine_reliability.
- ↑ Sharp, Tim (October 2018). "Saturn V Rockets & Apollo Spacecraft" (in en). https://www.space.com/16698-apollo-spacecraft.html.
- ↑ "Vanguard". http://www.astronautix.com/v/vanguard.html.
- ↑ "Atlas V Launch Services User's Guide". https://www.ulalaunch.com/docs/default-source/rockets/atlasvusersguide2010.pdf.
- ↑ "Falcon User's Guide". https://www.spacex.com/media/falcon-users-guide-2021-08.pdf.
ja:ロケット#多段式ロケット
 |
