Chemistry:Fullerene

From HandWiki
(Redirected from Chemistry:C20 fullerene)
Short description: Allotrope of carbons
Model of the C60 fullerene (buckminsterfullerene).
Model of the C20 fullerene.
Model of a carbon nanotube.
C60 fullerite (bulk solid C60).
Part of a series of articles on
Nanomaterials
C60-rods.png
Carbon nanotubes
Fullerenes
Other nanoparticles
Nanostructured materials

A fullerene is an allotrope of carbon whose molecules consist of carbon atoms connected by single and double bonds so as to form a closed or partially closed mesh, with fused rings of five to seven atoms. The molecules may be hollow spheres, ellipsoids, tubes, or other shapes.

Fullerenes with a closed mesh topology are informally denoted by their empirical formula Cn, often written Cn, where n is the number of carbon atoms. However, for some values of n there may be more than one isomer.

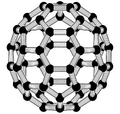
The family is named after buckminsterfullerene (C60), the most famous member, which in turn is named after Buckminster Fuller. The closed fullerenes, especially C60, are also informally called buckyballs for their resemblance to the standard ball of association football ("soccer"). Nested closed fullerenes have been named bucky onions. Cylindrical fullerenes are also called carbon nanotubes or buckytubes.[1] The bulk solid form of pure or mixed fullerenes is called fullerite.[2]

Fullerenes had been predicted for some time, but only after their accidental synthesis in 1985 were they detected in nature[3][4] and outer space.[5][6] The discovery of fullerenes greatly expanded the number of known allotropes of carbon, which had previously been limited to graphite, diamond, and amorphous carbon such as soot and charcoal. They have been the subject of intense research, both for their chemistry and for their technological applications, especially in materials science, electronics, and nanotechnology.[7]

Definition

IUPAC defines fullerenes as "polyhedral closed cages made up entirely of n three-coordinate carbon atoms and having 12 pentagonal and (n/2-10) hexagonal faces, where n ≥ 20."[8]

History

The icosahedral fullerene C540, another member of the family of fullerenes

Predictions and limited observations

The icosahedral C60H60 cage was mentioned in 1965 as a possible topological structure.[9] Eiji Osawa predicted the existence of C60 in 1970.[10][11] He noticed that the structure of a corannulene molecule was a subset of the shape of a football, and hypothesised that a full ball shape could also exist. Japanese scientific journals reported his idea, but neither it nor any translations of it reached Europe or the Americas.

Also in 1970, R.W.Henson (then of the United Kingdom Atomic Energy Research Establishment) proposed the C60 structure and made a model of it. Unfortunately, the evidence for that new form of carbon was very weak at the time, so the proposal was met with skepticism, and was never published. It was acknowledged only in 1999.[12][13]

In 1973, independently from Henson, D. A. Bochvar and E. G. Galpern made a quantum-chemical analysis of the stability of C60 and calculated its electronic structure. The paper was published in 1973,[14] but the scientific community did not give much importance to this theoretical prediction.

Around 1980, Sumio Iijima identified the molecule of C60 from an electron microscope image of carbon black, where it formed the core of a particle with the structure of a "bucky onion".[15]

Also in the 1980s at MIT, Mildred Dresselhaus and Morinobu Endo, collaborating with T. Venkatesan, directed studies blasting graphite with lasers, producing carbon clusters of atoms, which would be later identified as "fullerenes."[16]

Discovery of C60

In 1985, Harold Kroto of the University of Sussex, working with James R. Heath, Sean O'Brien, Robert Curl and Richard Smalley from Rice University, discovered fullerenes in the sooty residue created by vaporising carbon in a helium atmosphere. In the mass spectrum of the product, discrete peaks appeared corresponding to molecules with the exact mass of sixty or seventy or more carbon atoms, namely C60 and C70. The team identified their structure as the now familiar "buckyballs".[17]

The name "buckminsterfullerene" was eventually chosen for C60 by the discoverers as an homage to American architect Buckminster Fuller for the vague similarity of the structure to the geodesic domes which he popularized; which, if they were extended to a full sphere, would also have the icosahedral symmetry group.[18] The "ene" ending was chosen to indicate that the carbons are unsaturated, being connected to only three other atoms instead of the normal four. The shortened name "fullerene" eventually came to be applied to the whole family.

Kroto, Curl, and Smalley were awarded the 1996 Nobel Prize in Chemistry[19] for their roles in the discovery of this class of molecules.

Further developments

Kroto and the Rice team already discovered other fullerenes besides C60,[17] and the list was much expanded in the following years. Carbon nanotubes were first discovered and synthesized in 1991.[20][21]

After their discovery, minute quantities of fullerenes were found to be produced in sooty flames,[22] and by lightning discharges in the atmosphere.[4] In 1992, fullerenes were found in a family of mineraloids known as shungites in Karelia, Russia.[3]

The production techniques were improved by many scientists, including Donald Huffman, Wolfgang Krätschmer, Lowell D. Lamb, and Konstantinos Fostiropoulos.[23] Thanks to their efforts, by 1990 it was relatively easy to produce gram-sized samples of fullerene powder. Fullerene purification remains a challenge to chemists and to a large extent determines fullerene prices.

In 2010, the spectral signatures of C60 and C70 were observed by NASA's Spitzer infrared telescope in a cloud of cosmic dust surrounding a star 6500 light years away.[5] Kroto commented: "This most exciting breakthrough provides convincing evidence that the buckyball has, as I long suspected, existed since time immemorial in the dark recesses of our galaxy."[6] According to astronomer Letizia Stanghellini, "It’s possible that buckyballs from outer space provided seeds for life on Earth."[24] In 2019, ionized C60 molecules were detected with the Hubble Space Telescope in the space between those stars.[25][26]

Types

There are two major families of fullerenes, with fairly distinct properties and applications: the closed buckyballs and the open-ended cylindrical carbon nanotubes.[27] However, hybrid structures exist between those two classes, such as carbon nanobuds — nanotubes capped by hemispherical meshes or larger "buckybuds".

Buckyballs

C60 with isosurface of ground state electron density as calculated with DFT
Rotating view of C60, one kind of fullerene

Buckminsterfullerene

Main page: Chemistry:Buckminsterfullerene

Buckminsterfullerene is the smallest fullerene molecule containing pentagonal and hexagonal rings in which no two pentagons share an edge (which can be destabilizing, as in pentalene). It is also most common in terms of natural occurrence, as it can often be found in soot.

The empirical formula of buckminsterfullerene is C60 and its structure is a truncated icosahedron, which resembles an association football ball of the type made of twenty hexagons and twelve pentagons, with a carbon atom at the vertices of each polygon and a bond along each polygon edge.

The van der Waals diameter of a buckminsterfullerene molecule is about 1.1 nanometers (nm).[28] The nucleus to nucleus diameter of a buckminsterfullerene molecule is about 0.71 nm.

The buckminsterfullerene molecule has two bond lengths. The 6:6 ring bonds (between two hexagons) can be considered "double bonds" and are shorter than the 6:5 bonds (between a hexagon and a pentagon). Its average bond length is 1.4 Å.

Other fullerenes

Another fairly common fullerene has empirical formula C70,[29] but fullerenes with 72, 76, 84 and even up to 100 carbon atoms are commonly obtained.

The smallest possible fullerene is the dodecahedral C20. There are no fullerenes with 22 vertices.[30] The number of different fullerenes C2n grows with increasing n = 12, 13, 14, ..., roughly in proportion to n9 (sequence A007894 in the OEIS). For instance, there are 1812 non-isomorphic fullerenes C60. Note that only one form of C60, buckminsterfullerene, has no pair of adjacent pentagons (the smallest such fullerene). To further illustrate the growth, there are 214,127,713 non-isomorphic fullerenes C200, 15,655,672 of which have no adjacent pentagons. Optimized structures of many fullerene isomers are published and listed on the web.[31]

Heterofullerenes have heteroatoms substituting carbons in cage or tube-shaped structures. They were discovered in 1993[32] and greatly expand the overall fullerene class of compounds and can have dangling bonds on their surfaces. Notable examples include boron, nitrogen (azafullerene), oxygen, and phosphorus derivatives.

Carbon nanotubes

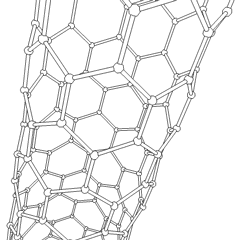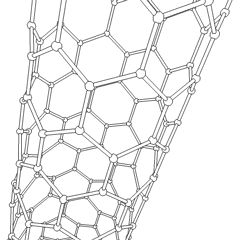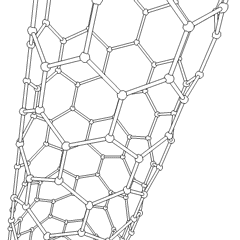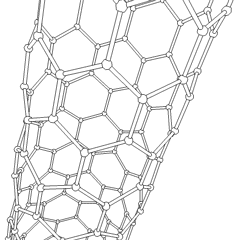
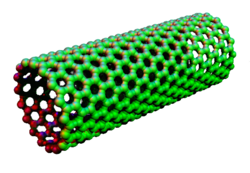
This rotating model of a carbon nanotube shows its 3D structure.

Carbon nanotubes are cylindrical fullerenes. These tubes of carbon are usually only a few nanometres wide, but they can range from less than a micrometer to several millimeters in length. They often have closed ends, but can be open-ended as well. There are also cases in which the tube reduces in diameter before closing off. Their unique molecular structure results in extraordinary macroscopic properties, including high tensile strength, high electrical conductivity, high ductility, high heat conductivity, and relative chemical inactivity (as it is cylindrical and "planar" — that is, it has no "exposed" atoms that can be easily displaced). One proposed use of carbon nanotubes is in paper batteries, developed in 2007 by researchers at Rensselaer Polytechnic Institute.[33] Another highly speculative proposed use in the field of space technologies is to produce high-tensile carbon cables required by a space elevator.

Derivatives

Buckyballs and carbon nanotubes have been used as building blocks for a great variety of derivatives and larger structures, such as[27]

  • Nested buckyballs ("carbon nano-onions" or "buckyonions")[34] proposed for lubricants;[35]
  • Nested carbon nanotubes ("carbon megatubes")[36]
  • Linked "ball-and-chain" dimers (two buckyballs linked by a carbon chain)[37]
  • Rings of buckyballs linked together.[38]

Heterofullerenes and non-carbon fullerenes

After the discovery of C60, many fullerenes have been synthesized (or studied theoretically by molecular modeling methods) in which some or all the carbon atoms are replaced by other elements. Non-carbon nanotubes, in particular, have attracted much attention.

Boron

A type of buckyball which uses boron atoms, instead of the usual carbon, was predicted and described in 2007. The B80 structure, with each atom forming 5 or 6 bonds, was predicted to be more stable than the C60 buckyball.[39] However, subsequent analysis found that the predicted Ih symmetric structure was vibrationally unstable and the resulting cage would undergo a spontaneous symmetry break, yielding a puckered cage with rare Th symmetry (symmetry of a volleyball).[40] The number of six-member rings in this molecule is 20 and number of five-member rings is 12. There is an additional atom in the center of each six-member ring, bonded to each atom surrounding it. By employing a systematic global search algorithm, it was later found that the previously proposed b80 fullerene is not a global maximum for 80-atom boron clusters and hence can not be found in nature; the most stable configurations have complex.[41] The same paper concluded that boron's energy landscape, unlike others, has many disordered low-energy structures, hence pure boron fullerenes are unlikely to exist in nature.[41]

However, an irregular B40 complex dubbed borospherene was prepared in 2014. This complex has two hexagonal faces and four heptagonal faces with in D2d symmetry interleaved with a network of 48 triangles.[42]

Other elements

Inorganic (carbon-free) fullerene-type structures have been built with the molybdenum(IV) sulfide (MoS2), long used as a graphite-like lubricant, tungsten (WS2), titanium (TiS2) and niobium (NbS2). These materials were found to be stable up to at least 350 tons/cm2 (34.3 GPa).[43]

Icosahedral or distorted-icosahedral fullerene-like complexes have also been prepared for germanium, tin, and lead; some of these complexes are spacious enough to hold most transition metal atoms.[44][45]

Main fullerenes

Below is a table of main closed carbon fullerenes synthesized and characterized so far, with their CAS number when known.[46] Fullerenes with fewer than 60 carbon atoms have been called "lower fullerenes",[47] and those with more than 70 atoms "higher fullerenes".[48]

Formula Num.
Isom.[1]		 Mol.
Symm.		 Cryst.
Symm.		 Space group No Pearson
symbol		 a (nm) b (nm) c (nm) β° Z ρ
(g/cm3)
C20 1 Ih
C60 1 Ih
C70 1 D5h
C72 1 D6h
C74 1 D3h
C76 2 D2* Monoclinic P21 4 mP2 1.102 1.108 1.768 108.10 2 1.48
Cubic Fm3m 225 cF4 1.5475 1.5475 1.5475 90 4 1.64
C78 5 D2v
C80 7
C82 9 C2, C2v, C3v Monoclinic P21 4 mP2 1.141 1.1355 1.8355 108.07 2
C84 24 D2*, D2d Cubic Fm3m 1.5817[49] 1.5817 1.5817 90
C86 19
C88 35
C90 46
C3996

In the table, "Num.Isom." is the number of possible isomers within the "isolated pentagon rule", which states that two pentagons in a fullerene should not share edges.[50][51] "Mol.Symm." is the symmetry of the molecule,[51][52] whereas "Cryst.Symm." is that of the crystalline framework in the solid state. Both are specified for the most experimentally abundant form(s). The asterisk * marks symmetries with more than one chiral form.

When C76 or C82 crystals are grown from toluene solution they have a monoclinic symmetry. The crystal structure contains toluene molecules packed between the spheres of the fullerene. However, evaporation of the solvent from C76 transforms it into a face-centered cubic form.[53] Both monoclinic and face-centered cubic (fcc) phases are known for better-characterized C60 and C70 fullerenes.

Properties

Topology

Schlegel diagrams are often used to clarify the 3D structure of closed-shell fullerenes, as 2D projections are often not ideal in this sense.[54]

In mathematical terms, the combinatorial topology (that is, the carbon atoms and the bonds between them, ignoring their positions and distances) of a closed-shell fullerene with a simple sphere-like mean surface (orientable, genus zero) can be represented as a convex polyhedron; more precisely, its one-dimensional skeleton, consisting of its vertices and edges. The Schlegel diagram is a projection of that skeleton onto one of the faces of the polyhedron, through a point just outside that face; so that all other vertices project inside that face.

  • Schlegel diagrams of some fullerenes

  • C20
    (dodecahedron)

  • C26

  • C60
    (truncated icosahedron)

  • C70

The Schlegel diagram of a closed fullerene is a graph that is planar and 3-regular (or "cubic"; meaning that all vertices have degree 3).

A closed fullerene with sphere-like shell must have at least some cycles that are pentagons or heptagons. More precisely, if all the faces have 5 or 6 sides, it follows from Euler's polyhedron formula, V−E+F=2 (where V, E, F are the numbers of vertices, edges, and faces), that V must be even, and that there must be exactly 12 pentagons and V/2−10 hexagons. Similar constraints exist if the fullerene has heptagonal (seven-atom) cycles.[55]

Bonding

Since each carbon atom is connected to only three neighbors, instead of the usual four, it is customary to describe those bonds as being a mixture of single and double covalent bonds. The hybridization of carbon in C60 has been reported to be sp2.01.[56] The bonding state can be analyzed by Raman spectroscopy, IR spectroscopy and X-ray photoelectron spectroscopy.[56][57]

Encapsulation

Additional atoms, ions, clusters, or small molecules can be trapped inside fullerenes to form inclusion compounds known as endohedral fullerenes. An unusual example is the egg-shaped fullerene Tb3N@C84, which violates the isolated pentagon rule.[58] Evidence for a meteor impact at the end of the Permian period was found by analyzing noble gases preserved by being trapped in fullerenes.[59]

Research

In the field of nanotechnology, heat resistance and superconductivity are some of the more heavily studied properties.

There are many calculations that have been done using ab-initio quantum methods applied to fullerenes. By DFT and TD-DFT methods one can obtain IR, Raman and UV spectra. Results of such calculations can be compared with experimental results.

Fullerene is an unusual reactant in many organic reactions such as the Bingel reaction discovered in 1993.

Aromaticity

Researchers have been able to increase the reactivity of fullerenes by attaching active groups to their surfaces. Buckminsterfullerene does not exhibit "superaromaticity": that is, the electrons in the hexagonal rings do not delocalize over the whole molecule.

A spherical fullerene of n carbon atoms has n pi-bonding electrons, free to delocalize. These should try to delocalize over the whole molecule. The quantum mechanics of such an arrangement should be like only one shell of the well-known quantum mechanical structure of a single atom, with a stable filled shell for n = 2, 8, 18, 32, 50, 72, 98, 128, etc. (i.e., twice a perfect square number), but this series does not include 60. This 2(N + 1)2 rule (with N integer) for spherical aromaticity is the three-dimensional analogue of Hückel's rule. The 10+ cation would satisfy this rule, and should be aromatic. This has been shown to be the case using quantum chemical modelling, which showed the existence of strong diamagnetic sphere currents in the cation.[60]

As a result, C60 in water tends to pick up two more electrons and become an anion. The nC60 described below may be the result of C60 trying to form a loose metallic bond.

Reactions

Polymerization

Under high pressure and temperature, buckyballs collapse to form various one-, two-, or three-dimensional carbon frameworks. Single-strand polymers are formed using the Atom Transfer Radical Addition Polymerization (ATRAP) route.[61]

"Ultrahard fullerite" is a coined term frequently used to describe material produced by high-pressure high-temperature (HPHT) processing of fullerite. Such treatment converts fullerite into a nanocrystalline form of diamond which has been reported to exhibit remarkable mechanical properties.[62]

Fullerite (scanning electron microscope image)

Chemistry

Main page: Chemistry:Fullerene chemistry

Fullerenes are stable, but not totally unreactive. The sp2-hybridized carbon atoms, which are at their energy minimum in planar graphite, must be bent to form the closed sphere or tube, which produces angle strain. The characteristic reaction of fullerenes is electrophilic addition at 6,6-double bonds, which reduces angle strain by changing sp2-hybridized carbons into sp3-hybridized ones. The change in hybridized orbitals causes the bond angles to decrease from about 120° in the sp2 orbitals to about 109.5° in the sp3 orbitals. This decrease in bond angles allows for the bonds to bend less when closing the sphere or tube, and thus, the molecule becomes more stable.

Solubility

C60 in solution
C60 in extra virgin olive oil, showing the characteristic purple color of pristine C60 solutions

Fullerenes are soluble in many organic solvents, such as toluene, chlorobenzene, and 1,2,3-trichloropropane. Solubilities are generally rather low, such as 8 g/L for C60 in carbon disulfide. Still, fullerenes are the only known allotrope of carbon that can be dissolved in common solvents at room temperature.[63][64][65][66][67] Among the best solvents is 1-chloronaphthalene, which will dissolve 51 g/L of C60.

Solutions of pure buckminsterfullerene have a deep purple color. Solutions of C70 are a reddish brown. The higher fullerenes C76 to C84 have a variety of colors.

Millimeter-sized crystals of C60 and C70, both pure and solvated, can be grown from benzene solution. Crystallization of C60 from benzene solution below 30 °C (when solubility is maximum) yields a triclinic solid solvate C60·4C6H6. Above 30 °C one obtains solvate-free fcc C60.[68][69]

Quantum mechanics

In 1999, researchers from the University of Vienna demonstrated that wave-particle duality applied to molecules such as fullerene.[70]

Superconductivity

Main page: Chemistry:Buckminsterfullerene

Fullerenes are normally electrical insulators, but when crystallized with alkali metals, the resultant compound can be conducting or even superconducting.[71]

Chirality

Some fullerenes (e.g. C76, C78, C80, and C84) are inherently chiral because they are D2-symmetric, and have been successfully resolved. Research efforts are ongoing to develop specific sensors for their enantiomers.

Stability

Two theories have been proposed to describe the molecular mechanisms that make fullerenes. The older, “bottom-up” theory proposes that they are built atom-by-atom. The alternative “top-down” approach claims that fullerenes form when much larger structures break into constituent parts.[72]

In 2013 researchers discovered that asymmetrical fullerenes formed from larger structures settle into stable fullerenes. The synthesized substance was a particular metallofullerene consisting of 84 carbon atoms with two additional carbon atoms and two yttrium atoms inside the cage. The process produced approximately 100 micrograms.[72]

However, they found that the asymmetrical molecule could theoretically collapse to form nearly every known fullerene and metallofullerene. Minor perturbations involving the breaking of a few molecular bonds cause the cage to become highly symmetrical and stable. This insight supports the theory that fullerenes can be formed from graphene when the appropriate molecular bonds are severed.[72][73]

Systematic naming

According to the IUPAC, to name a fullerene, one must cite the number of member atoms for the rings which comprise the fullerene, its symmetry point group in the Schoenflies notation, and the total number of atoms. For example, buckminsterfullerene C60 is systematically named (C60-Ih)[5,6]fullerene. The name of the point group should be retained in any derivative of said fullerene, even if that symmetry is lost by the derivation.

To indicate the position of substituted or attached elements, the fullerene atoms are usually numbered in a spiral path, usually starting with the ring on one of the main axes. If the structure of the fullerene does not allow such numbering, another starting atom was chosen to still achieve a spiral path sequence.

The latter is the case for C70, which is (C70-D5h(6))[5,6]fullerene in IUPAC notation. The symmetry D5h(6) means that this is the isomer where the C5 axis goes through a pentagon surrounded by hexagons rather than pentagons.[54]

  • (C60-Ih)[5,6]fullerene
    Carbon numbering.

  • (C70-D5h(6))[5,6]fullerene
    Carbon numbering.

  • (C70-D5h(6))[5,6]fullerene
    Non-equivalent bonds shown by different colours.

  • 3'H-Cyclopropa[1,2](C70-D5h(6))[5,6]fullerene.

  • 3'H-Cyclopropa[2,12](C70-D5h(6))[5,6]fullerene.

  • C71-PCBM, [1,2]-isomer.
    IUPAC name is methyl 4-(3’-phenyl-3’H-cyclopropa[1,2](C70-D5h(6))[5,6]fullerene-3’-yl)butyrate.

In IUPAC's nomenclature, fully saturated analogues of fullerenes are called fulleranes. If the mesh has other element(s) substituted for one or more carbons, the compound is named a heterofullerene. If a double bond is replaced by a methylene bridge –CH
2–, the resulting structure is a homofullerene. If an atom is fully deleted and missing valences saturated with hydrogen atoms, it is a norfullerene. When bonds are removed (both sigma and pi), the compound becomes secofullerene; if some new bonds are added in an unconventional order, it is a cyclofullerene.[54]

Production

Fullerene production generally starts by producing fullerene-rich soot. The original (and still current) method was to send a large electric current between two nearby graphite electrodes in an inert atmosphere. The resulting electric arc vaporizes the carbon into a plasma that then cools into sooty residue.[17] Alternatively, soot is produced by laser ablation of graphite or pyrolysis of aromatic hydrocarbons.[74][citation needed] Combustion of benzene is the most efficient process, developed at MIT.[75][76]

These processes yield a mixture of various fullerenes and other forms of carbon. The fullerenes are then extracted from the soot using appropriate organic solvents and separated by chromatography.[77]:p.369 One can obtain milligram quantities of fullerenes with 80 atoms or more. C76, C78 and C84 are available commercially.

Applications

Fullerenes have been extensively used for several biomedical applications including the design of high-performance MRI contrast agents, X-ray imaging contrast agents, photodynamic therapy and drug and gene delivery, summarized in several comprehensive reviews.[78]

Tumor research

While past cancer research has involved radiation therapy, photodynamic therapy is important to study because breakthroughs in treatments for tumor cells will give more options to patients with different conditions. Recent experiments using HeLa cells in cancer research involves the development of new photosensitizers with increased ability to be absorbed by cancer cells and still trigger cell death. It is also important that a new photosensitizer does not stay in the body for a long time to prevent unwanted cell damage.[79]

Fullerenes can be made to be absorbed by HeLa cells. The C60 derivatives can be delivered to the cells by using the functional groups L-phenylalanine, folic acid, and L-arginine among others.[80]

Functionalizing the fullerenes aims to increase the solubility of the molecule by the cancer cells. Cancer cells take up these molecules at an increased rate because of an upregulation of transporters in the cancer cell, in this case amino acid transporters will bring in the L-arginine and L-phenylalanine functional groups of the fullerenes.[81]

Once absorbed by the cells, the C60 derivatives would react to light radiation by turning molecular oxygen into reactive oxygen which triggers apoptosis in the HeLa cells and other cancer cells that can absorb the fullerene molecule. This research shows that a reactive substance can target cancer cells and then be triggered by light radiation, minimizing damage to surrounding tissues while undergoing treatment.[82]

When absorbed by cancer cells and exposed to light radiation, the reaction that creates reactive oxygen damages the DNA, proteins, and lipids that make up the cancer cell. This cellular damage forces the cancerous cell to go through apoptosis, which can lead to the reduction in size of a tumor. Once the light radiation treatment is finished the fullerene will reabsorb the free radicals to prevent damage of other tissues.[83] Since this treatment focuses on cancer cells, it is a good option for patients whose cancer cells are within reach of light radiation. As this research continues, the treatment may penetrate deeper into the body and be absorbed by cancer cells more effectively.[79]

Safety and toxicity

Main pages: Physics:Health and safety hazards of nanomaterials and Chemistry:Toxicology of carbon nanomaterials

In 2013, a comprehensive review on the toxicity of fullerene was published reviewing work beginning in the early 1990s to present and concluded that very little evidence gathered since the discovery of fullerenes indicate that C60 is toxic.[78] The toxicity of these carbon nanoparticles is not only dose- and time-dependent, but also depends on a number of other factors such as:

  • type (e.g.: C60, C70, M@C60, M@C82)
  • functional groups used to water-solubilize these nanoparticles (e.g.: OH, COOH)
  • method of administration (e.g.: intravenous, intraperitoneal)

It was recommended to assess the pharmacology of every new fullerene- or metallofullerene-based complex individually as a different compound.

Popular culture

Examples of fullerenes appear frequently in popular culture. Fullerenes appeared in fiction well before scientists took serious interest in them. In a humorously speculative 1966 column for New Scientist, David Jones suggested the possibility of making giant hollow carbon molecules by distorting a plane hexagonal net with the addition of impurity atoms.[84]

See also


References

  1. ↑ "Definition of BUCKYTUBE". https://www.merriam-webster.com/dictionary/buckytube. 
  2. ↑ "fullerite". https://eng.thesaurus.rusnano.com/wiki/article1935. 
  3. ↑ 3.0 3.1 Buseck, P.R.; Tsipursky, S.J.; Hettich, R. (1992). "Fullerenes from the Geological Environment". Science 257 (5067): 215–7. doi:10.1126/science.257.5067.215. PMID 17794751. Bibcode: 1992Sci...257..215B. 
  4. ↑ 4.0 4.1 "The allotropes of carbon". http://invsee.asu.edu/nmodules/Carbonmod/everywhere.html. 
  5. ↑ 5.0 5.1 Cami, J; Bernard-Salas, J.; Peeters, E.; Malek, S. E. (2 September 2010). "Detection of C60 and C70 in a Young Planetary Nebula". Science 329 (5996): 1180–1182. doi:10.1126/science.1192035. PMID 20651118. 
  6. ↑ 6.0 6.1 Stars reveal carbon 'spaceballs', BBC, 22 July 2010.
  7. ↑ Belkin, A.; et., al. (2015). "Self-Assembled Wiggling Nano-Structures and the Principle of Maximum Entropy Production". Sci. Rep. 5: 8323. doi:10.1038/srep08323. PMID 25662746. Bibcode: 2015NatSR...5E8323B. 
  8. ↑ Godly, E.W.; Taylor, R. (1997). "Nomenclature and Terminology of Fullerenes". Pure and Applied Chemistry 69 (7): 1411–1434. doi:10.1351/pac199769071411. https://publications.iupac.org/pac/1997/pdf/6907x1411.pdf. 
  9. ↑ Schultz, H.P. (1965). "Topological Organic Chemistry. Polyhedranes and Prismanes". Journal of Organic Chemistry 30 (5): 1361–1364. doi:10.1021/jo01016a005. 
  10. ↑ Osawa, E. (1970). "Superaromaticity". Kagaku 25: 854–863. 
  11. ↑ Halford, B. (9 October 2006). "The World According to Rick". Chemical & Engineering News 84 (41): 13–19. doi:10.1021/cen-v084n041.p013. http://pubs.acs.org/cen/coverstory/84/8441cover.html. 
  12. ↑ Thrower, P.A. (1999). "Editorial". Carbon 37 (11): 1677–1678. doi:10.1016/S0008-6223(99)00191-8. 
  13. ↑ Henson, R.W.. "The History of Carbon 60 or Buckminsterfullerene". http://www.solina.demon.co.uk/c60.htm. 
  14. ↑ Bochvar, D.A.; Galpern, E.G. (1973). "О гипотетических системах: карбододекаэдре, s-икосаэдре и карбо-s-икосаэдре". Dokl. Akad. Nauk SSSR 209: 610. 
  15. ↑ Iijima, S (1980). "Direct observation of the tetrahedral bonding in graphitized carbon black by high resolution electron microscopy". Journal of Crystal Growth 50 (3): 675–683. doi:10.1016/0022-0248(80)90013-5. Bibcode: 1980JCrGr..50..675I. 
  16. ↑ "Mildred S. Dresselhaus" (in en). 2016-10-05. https://www.fi.edu/laureates/mildred-s-dresselhaus. 
  17. ↑ 17.0 17.1 17.2 Kroto, H.W.; Heath, J. R.; Obrien, S. C. et al. (1985). "C60: Buckminsterfullerene". Nature 318 (6042): 162–163. doi:10.1038/318162a0. Bibcode: 1985Natur.318..162K. 
  18. ↑ Buckminsterfullerene, C60. Sussex Fullerene Group. chm.bris.ac.uk
  19. ↑ "The Nobel Prize in Chemistry 1996". https://www.nobelprize.org/nobel_prizes/chemistry/laureates/1996/. 
  20. ↑ Mraz, S.J. (14 April 2005). "A new buckyball bounces into town". http://machinedesign.com/ContentItem/60618/Anewbuckyballbouncesintotown.aspx. 
  21. ↑ Iijima, Sumio (1991). "Helical microtubules of graphitic carbon". Nature 354 (6348): 56–58. doi:10.1038/354056a0. Bibcode: 1991Natur.354...56I. 
  22. ↑ Reilly, P. T. A.; Gieray, R. A.; Whitten, W. B.; Ramsey, J. M. (2000). "Fullerene Evolution in Flame-Generated Soot". Journal of the American Chemical Society 122 (47): 11596–11601. doi:10.1021/ja003521v. ISSN 0002-7863. 
  23. ↑ Krätschmer, W.; Lamb, Lowell D.; Fostiropoulos, K.; Huffman, Donald R. (1990). "Solid C60: a new form of carbon" (in en). Nature 347 (6291): 354–358. doi:10.1038/347354a0. ISSN 0028-0836. Bibcode: 1990Natur.347..354K. http://www.nature.com/articles/347354a0. 
  24. ↑ Atkinson, Nancy (27 October 2010). "Buckyballs Could Be Plentiful in the Universe". Universe Today. http://www.universetoday.com/76732/buckyballs-could-be-plentiful-in-the-universe. 
  25. ↑ Starr, Michelle (29 April 2019). "The Hubble Space Telescope Has Just Found Solid Evidence of Interstellar Buckyballs". ScienceAlert.com. https://www.sciencealert.com/the-hubble-space-telescope-has-found-evidence-of-interstellar-buckyballs. 
  26. ↑ Cordiner, M.A. (22 April 2019). "Confirming Interstellar C60 + Using the Hubble Space Telescope". The Astrophysical Journal Letters 875 (2): L28. doi:10.3847/2041-8213/ab14e5. Bibcode: 2019ApJ...875L..28C. 
  27. ↑ 27.0 27.1 Miessler, G.L.; Tarr, D.A. (2004). Inorganic Chemistry (3rd ed.). Pearson Education. ISBN 978-0-13-120198-9. https://archive.org/details/inorganicchemist03edmies. 
  28. ↑ Qiao, Rui; Roberts, Aaron P.; Mount, Andrew S. et al. (2007). "Translocation of C60 and Its Derivatives Across a Lipid Bilayer". Nano Letters 7 (3): 614–9. doi:10.1021/nl062515f. PMID 17316055. Bibcode: 2007NanoL...7..614Q. 
  29. ↑ Locke, W. (13 October 1996). "Buckminsterfullerene: Molecule of the Month". Imperial College. http://www.bristol.ac.uk/Depts/Chemistry/MOTM/buckyball/c60a.htm. 
  30. ↑ Meija, Juris (2006). "Goldberg Variations Challenge". Analytical and Bioanalytical Chemistry 385 (1): 6–7. doi:10.1007/s00216-006-0358-9. PMID 16598460. https://www.springer.com/cda/content/document/cda_downloaddocument.pdf?SGWID=0-0-45-275900-0. 
  31. ↑ Fowler, P. W. and Manolopoulos, D. E. Cn Fullerenes. nanotube.msu.edu
  32. ↑ Harris, D.J. "Discovery of Nitroballs: Research in Fullerene Chemistry" http://www.usc.edu/CSSF/History/1993/CatWin_S05.html
  33. ↑ Pushparaj, V.L.; Shaijumon, Manikoth M.; Kumar, A. et al. (2007). "Flexible energy storage devices based on nanocomposite paper". Proceedings of the National Academy of Sciences 104 (34): 13574–7. doi:10.1073/pnas.0706508104. PMID 17699622. Bibcode: 2007PNAS..10413574P. 
  34. ↑ Ugarte, D. (1992). "Curling and closure of graphitic networks under electron-beam irradiation". Nature 359 (6397): 707–709. doi:10.1038/359707a0. PMID 11536508. Bibcode: 1992Natur.359..707U. 
  35. ↑ Sano, N.; Wang, H.; Chhowalla, M. et al. (2001). "Synthesis of carbon 'onions' in water". Nature 414 (6863): 506–7. doi:10.1038/35107141. PMID 11734841. Bibcode: 2001Natur.414..506S. 
  36. ↑ Mitchel, D.R.; Brown, R. Malcolm Jr. (2001). "The Synthesis of Megatubes: New Dimensions in Carbon Materials". Inorganic Chemistry 40 (12): 2751–5. doi:10.1021/ic000551q. PMID 11375691. 
  37. ↑ Shvartsburg, A.A.; Hudgins, R. R.; Gutierrez, Rafael et al. (1999). "Ball-and-Chain Dimers from a Hot Fullerene Plasma". Journal of Physical Chemistry A 103 (27): 5275–5284. doi:10.1021/jp9906379. Bibcode: 1999JPCA..103.5275S. http://www.indiana.edu/~nano/publications/1999/Ball_and_Chain_Dimers_from_a_Hot_Fullerene_Plasma.pdf. 
  38. ↑ Li, Y.; Huang, Y.; Du, Shixuan; Liu, Ruozhuang (2001). "Structures and stabilities of C60-rings". Chemical Physics Letters 335 (5–6): 524–532. doi:10.1016/S0009-2614(01)00064-1. Bibcode: 2001CPL...335..524L. 
  39. ↑ Gonzalez Szwacki, N.; Sadrzadeh, A.; Yakobson, B. (2007). "B80 Fullerene: An Ab Initio Prediction of Geometry, Stability, and Electronic Structure". Physical Review Letters 98 (16): 166804. doi:10.1103/PhysRevLett.98.166804. PMID 17501448. Bibcode: 2007PhRvL..98p6804G. 
  40. ↑ Gopakumar, G.; Nguyen, M.T.; Ceulemans, A. (2008). "The boron buckyball has an unexpected Th symmetry". Chemical Physics Letters 450 (4–6): 175–177. doi:10.1016/j.cplett.2007.11.030. Bibcode: 2008CPL...450..175G. 
  41. ↑ 41.0 41.1 De, S.; Willand, A.; Amsler, M. et al. (2011). "Energy Landscape of Fullerene Materials: A Comparison of Boron to Boron Nitride and Carbon". Physical Review Letters 106 (22): 225502. doi:10.1103/PhysRevLett.106.225502. PMID 21702613. Bibcode: 2011PhRvL.106v5502D. 
  42. ↑ Zhai, Hua-Jin; Ya-Fan Zhao; Wei-Li Li et al. (2014-07-13). "Observation of an all-boron fullerene". Nature Chemistry 6 (8): 727–731. doi:10.1038/nchem.1999. ISSN 1755-4349. PMID 25054944. Bibcode: 2014NatCh...6..727Z. 
  43. ↑ Genuth, Iddo; Yaffe, Tomer (February 15, 2006). "Protecting the soldiers of tomorrow". IsraCast. http://www.isracast.com/article.aspx?id=28. 
  44. ↑ Cui, Li-Feng; Xin Huang; Lei-Ming Wang et al. (2006-07-01). "Sn122-: Stannaspherene". Journal of the American Chemical Society 128 (26): 8390–8391. doi:10.1021/ja062052f. ISSN 0002-7863. PMID 16802791. 
  45. ↑ Cui, Li-Feng; Xin Huang; Lei-Ming Wang et al. (2006-08-01). "Pb122-: Plumbaspherene". The Journal of Physical Chemistry A 110 (34): 10169–10172. doi:10.1021/jp063617x. ISSN 1089-5639. PMID 16928103. Bibcode: 2006JPCA..11010169C. 
  46. ↑ W. L. F. Armarego; Christina Li Lin Chai (11 May 2009). Purification of laboratory chemicals. Butterworth-Heinemann. pp. 214–. ISBN 978-1-85617-567-8. https://books.google.com/books?id=PTXyS7Yj6zUC&pg=PA214. Retrieved 26 December 2011. 
  47. ↑ Sun, Marc C. Nicklaus; Rui-hua, Xie (2005). "Structure, Stability, and NMR Properties of Lower Fullerenes C38−C50 and Azafullerene C44N6". J. Phys. Chem. 109 (20): 4617–4622. doi:10.1021/jp0450181. PMID 16833800. Bibcode: 2005JPCA..109.4617S. 
  48. ↑ Thilgen, Carlo; Herrmann, Andreas; Diederich, François (14 November 1997). "The Covalent Chemistry of Higher Fullerenes: C70 and Beyond". Angewandte Chemie International Edition in English 36 (21): 2268–2280. doi:10.1002/anie.199722681. 
  49. ↑ Margadonna, Serena; Brown, Craig M.; Dennis, T. John S. et al. (July 1998). "Crystal Structure of the Higher Fullerene C". Chemistry of Materials 10 (7): 1742–1744. doi:10.1021/cm980183c. 
  50. ↑ Manolopoulos, David E.; Fowler, Patrick W. (1991). "Structural proposals for endohedral metal-fullerene complexes". Chemical Physics Letters 187 (1–2): 1–7. doi:10.1016/0009-2614(91)90475-O. Bibcode: 1991CPL...187....1M. 
  51. ↑ 51.0 51.1 Diederich, Francois; Whetten, Robert L. (1992). "Beyond C60: The higher fullerenes". Accounts of Chemical Research 25 (3): 119. doi:10.1021/ar00015a004. 
  52. ↑ K Veera Reddy (1 January 1998). Symmetry And Spectroscopy Of Molecules. New Age International. pp. 126–. ISBN 978-81-224-1142-3. https://books.google.com/books?id=oZeFG6QDNekC&pg=PA126. Retrieved 26 December 2011. 
  53. ↑ Kawada, H.; Fujii, Y.; Nakao, H. et al. (1995). "Structural aspects of C82 and C76 crystals studied by x-ray diffraction". Physical Review B 51 (14): 8723–8730. doi:10.1103/PhysRevB.51.8723. PMID 9977506. 
  54. ↑ 54.0 54.1 54.2 Powell, W. H.; Cozzi, F.; Moss, G. P. et al. (2002). "Nomenclature for the C60-Ih and C70-D5h(6) Fullerenes (IUPAC Recommendations 2002)". Pure and Applied Chemistry 74 (4): 629–695. doi:10.1351/pac200274040629. http://doc.rero.ch/record/303076/files/pac200274040629.pdf. 
  55. ↑ "Fullerene", Encyclopædia Britannica on-line
  56. ↑ 56.0 56.1 Diana, Nooramalina; Yamada, Yasuhiro; Gohda, Syun et al. (2021-02-01). "Carbon materials with high pentagon density" (in en). Journal of Materials Science 56 (4): 2912–2943. doi:10.1007/s10853-020-05392-x. ISSN 1573-4803. Bibcode: 2021JMatS..56.2912D. https://doi.org/10.1007/s10853-020-05392-x. 
  57. ↑ Kim, Jungpil; Yamada, Yasuhiro; Kawai, Miki et al. (2015-10-01). "Spectral change of simulated X-ray photoelectron spectroscopy from graphene to fullerene" (in en). Journal of Materials Science 50 (20): 6739–6747. doi:10.1007/s10853-015-9229-0. ISSN 1573-4803. Bibcode: 2015JMatS..50.6739K. https://doi.org/10.1007/s10853-015-9229-0. 
  58. ↑ Beavers, C.M.; Zuo, T. (2006). "Tb3N@C84: An improbable, egg-shaped endohedral fullerene that violates the isolated pentagon rule". Journal of the American Chemical Society 128 (35): 11352–3. doi:10.1021/ja063636k. PMID 16939248. 
  59. ↑ Luann, B.; Poreda, Robert J.; Hunt, Andrew G. et al. (2007). "Impact Event at the Permian-Triassic Boundary: Evidence from Extraterrestrial Noble Gases in Fullerenes". Science 291 (5508): 1530–3. doi:10.1126/science.1057243. PMID 11222855. Bibcode: 2001Sci...291.1530B. 
  60. ↑ Johansson, M.P.; Jusélius, J.; Sundholm, D. (2005). "Sphere Currents of Buckminsterfullerene". Angewandte Chemie International Edition 44 (12): 1843–6. doi:10.1002/anie.200462348. PMID 15706578. 
  61. ↑ Hiorns, R.C.; Cloutet, Eric; Ibarboure, Emmanuel et al. (2010). "Synthesis of Donor-Acceptor Multiblock Copolymers Incorporating Fullerene Backbone Repeat Units". Macromolecules. 14 43 (14): 6033–6044. doi:10.1021/ma100694y. Bibcode: 2010MaMol..43.6033H. 
  62. ↑ Blank, V.; Popov, M.; Pivovarov, G. et al. (1998). "Ultrahard and superhard phases of fullerite C60: Comparison with diamond on hardness and wear". Diamond and Related Materials 7 (2–5): 427–431. doi:10.1016/S0925-9635(97)00232-X. Bibcode: 1998DRM.....7..427B. 
  63. ↑ Beck, Mihály T.; Mándi, Géza (1997). "Solubility of C60". Fullerenes, Nanotubes and Carbon Nanostructures 5 (2): 291–310. doi:10.1080/15363839708011993. 
  64. ↑ Bezmel'nitsyn, V.N.; Eletskii, A.V.; Okun', M.V. (1998). "Fullerenes in solutions". Physics-Uspekhi 41 (11): 1091–1114. doi:10.1070/PU1998v041n11ABEH000502. Bibcode: 1998PhyU...41.1091B. 
  65. ↑ Ruoff, R.S.; Tse, Doris S.; Malhotra, Ripudaman; Lorents, Donald C. (1993). "Solubility of fullerene (C60) in a variety of solvents". Journal of Physical Chemistry 97 (13): 3379–3383. doi:10.1021/j100115a049. http://bucky-central.me.utexas.edu/RuoffsPDFs/40.pdf. Retrieved 24 February 2015. 
  66. ↑ Sivaraman, N.; Dhamodaran, R.; Kaliappan, I. et al. (1994). "Solubility of C70 in Organic Solvents". Fullerene Science and Technology 2 (3): 233–246. doi:10.1080/15363839408009549. 
  67. ↑ Semenov, K. N.; Charykov, N. A.; Keskinov, V. A. et al. (2010). "Solubility of Light Fullerenes in Organic Solvents". Journal of Chemical & Engineering Data 55: 13–36. doi:10.1021/je900296s. 
  68. ↑ Talyzin, A.V. (1997). "Phase Transition C60−C60*4C6H6 in Liquid Benzene". Journal of Physical Chemistry B 101 (47): 9679–9681. doi:10.1021/jp9720303. 
  69. ↑ Talyzin, A.V.; Engström, I. (1998). "C70 in Benzene, Hexane, and Toluene Solutions". Journal of Physical Chemistry B 102 (34): 6477–6481. doi:10.1021/jp9815255. 
  70. ↑ Arndt, M.; Nairz, Olaf; Vos-Andreae, Julian et al. (1999). "Wave-particle duality of C60". Nature 401 (6754): 680–2. doi:10.1038/44348. PMID 18494170. Bibcode: 1999Natur.401..680A. http://www.qudev.ethz.ch/phys4/studentspresentations/waveparticle/arndt_c60molecules.pdf. 
  71. ↑ Katz, E. A. (2006). "Fullerene Thin Films as Photovoltaic Material". in Sōga, Tetsuo. Nanostructured materials for solar energy conversion. Elsevier. pp. 372, 381. ISBN 978-0-444-52844-5. https://books.google.com/books?id=GmQR1tuk5IgC&pg=PA361. 
  72. ↑ 72.0 72.1 72.2 Support for top-down theory of how 'buckyballs’ form. kurzweilai.net. 24 September 2013
  73. ↑ Zhang, J.; Bowles, F. L.; Bearden, D. W. et al. (2013). "A missing link in the transformation from asymmetric to symmetric metallofullerene cages implies a top-down fullerene formation mechanism". Nature Chemistry 5 (10): 880–885. doi:10.1038/nchem.1748. PMID 24056346. Bibcode: 2013NatCh...5..880Z. 
  74. ↑ Bobrowsky, Maciej (2019-10-01). "Nanostructures and computer simulations in material science". http://www.mif.pg.gda.pl/homepages/mate/Nanochemistry/nanochem_lect_10.pdf. 
  75. ↑ Osawa, Eiji (2002). Perspectives of Fullerene Nanotechnology. Springer Science & Business Media. p. 29. ISBN 978-0-7923-7174-8. https://books.google.com/books?id=8GjOboiuVW0C&pg=PA29. 
  76. ↑ Arikawa, Mineyuki (2006). "Fullerenes—an attractive nano carbon material and its production technology.". Nanotechnology Perceptions 2 (3): 121–128. ISSN 1660-6795. 
  77. ↑ Katz, E. A. (2006). "Fullerene Thin Films as Photovoltaic Material". in Sōga, Tetsuo. Nanostructured materials for solar energy conversion. Elsevier. pp. 361–443. doi:10.1016/B978-044452844-5/50014-7. ISBN 978-0-444-52844-5. https://books.google.com/books?id=GmQR1tuk5IgC&pg=PA361. 
  78. ↑ 78.0 78.1 G. Lalwani and B. Sitharaman, Multifunctional fullerene and metallofullerene based nanobiomaterials, NanoLIFE 08/2013; 3:1342003. DOI: 10.1142/S1793984413420038 Full Text PDF
  79. ↑ 79.0 79.1 Brown, S.B.; Brown, E.A.; Walker, I. (2004). "The present and future role of photodynamic therapy in cancer treatment". Lancet Oncology 5 (8): 497–508. doi:10.1016/S1470-2045(04)01529-3. PMID 15288239. 
  80. ↑ Mroz, Pawel; Pawlak, Anna; Satti, Minahil et al. (2007). "Functionalized fullerenes mediate photodynamic killing of cancer cells: type I versus typee II photochemical mechanism". Free Radical Biology & Medicine 43 (5): 711–719. doi:10.1016/j.freeradbiomed.2007.05.005. PMID 17664135. 
  81. ↑ Ganapathy, Vadivel; Thanaraju, Muthusamy; Prasad, Puttur D. (2009). "Nutrient transporters in cancer: Relevance to Warburg hypothesis and beyond". Pharmacology & Therapeutics 121 (1): 29–40. doi:10.1016/j.pharmthera.2008.09.005. PMID 18992769. 
  82. ↑ Hu, Zhen; Zhang, Chunhua; Huang, Yudong et al. (2012). "Photodynamic anticancer activities of water-soluble C60 derivatives and their biological consequences in a HeLa cell line". Chemico-Biological Interactions 195 (1): 86–94. doi:10.1016/j.cbi.2011.11.003. PMID 22108244. 
  83. ↑ Markovic, Zoran; Trajkovic, Vladimir (2008). "Biomedical potential of the reactive oxygen species generation and quenching by fullerenes". Biomaterials 29 (26): 3561–3573. doi:10.1016/j.biomaterials.2008.05.005. PMID 18534675. 
  84. ↑ Jones, D. (1966). "Note in Ariadne column". New Scientist 32: 245. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Chemistry:Fullerene&oldid=3421183"