Circular prime
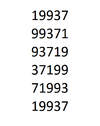 The numbers generated by cyclically permuting the digits of 19937. The first digit is removed and readded at the right side of the remaining string of digits. This process is repeated until the starting number is reached again. Since all intermediate numbers generated by this process are prime, 19937 is a circular prime. | |
| Named after | Circle |
|---|---|
| Publication year | 2004 |
| Author of publication | Darling, D. J. |
| No. of known terms | 27 |
| First terms | 2, 3, 5, 7, 11, 13, 17, 37, 79, 113, 197, 199 |
| Largest known term | (10^8177207-1)/9 |
| OEIS index |
|
A circular prime is a prime number with the property that the number generated at each intermediate step when cyclically permuting its (base 10) digits will be prime.[1][2] For example, 1193 is a circular prime, since 1931, 9311 and 3119 all are also prime.[3] A circular prime with at least two digits can only consist of combinations of the digits 1, 3, 7 or 9, because having 0, 2, 4, 6 or 8 as the last digit makes the number divisible by 2, and having 0 or 5 as the last digit makes it divisible by 5.[4] The complete listing of the smallest representative prime from all known cycles of circular primes (The single-digit primes and repunits are the only members of their respective cycles) is 2, 3, 5, 7, R2, 13, 17, 37, 79, 113, 197, 199, 337, 1193, 3779, 11939, 19937, 193939, 199933, R19, R23, R317, R1031, R49081, R86453, R109297, R270343, R5794777 and R8177207, where Rn is a repunit prime with n digits. There are no other circular primes up to 1023.[3] A type of prime related to the circular primes are the permutable primes, which are a subset of the circular primes (every permutable prime is also a circular prime, but not necessarily vice versa).[3]
Other bases
The complete listing of the smallest representative prime from all known cycles of circular primes in base 12 is (using inverted two and three for ten and eleven, respectively)
- 2, 3, 5, 7, Ɛ, R2, 15, 57, 5Ɛ, R3, 117, 11Ɛ, 175, 1Ɛ7, 157Ɛ, 555Ɛ, R5, 115Ɛ77, R17, R81, R91, R225, R255, R4ᘔ5, R5777, R879Ɛ, R198Ɛ1, R23175, and R311407.
where Rn is a repunit prime in base 12 with n digits. There are no other circular primes in base 12 up to 1212.
In base 2, only Mersenne primes can be circular primes, since any 0 permuted to the one's place results in an even number.
References
- ↑ The Universal Book of Mathematics, Darling, David J., 11 August 2004, p. 70, ISBN 9780471270478, https://books.google.com/books?id=nnpChqstvg0C&dq=circular+prime&pg=PA70, retrieved 25 July 2010
- ↑ Prime Numbers—The Most Mysterious Figures in Math, Wells, D., p. 47 (page 28 of the book), http://wenku.baidu.com/view/8d95d909581b6bd97f19ea85.html, retrieved 27 July 2010
- ↑ 3.0 3.1 3.2 Circular Primes, Patrick De Geest, http://www.worldofnumbers.com/circular.htm, retrieved 25 July 2010
- ↑ The mathematics of Oz: mental gymnastics from beyond the edge, Pickover, Clifford A., 2 September 2002, p. 330, ISBN 9780521016780, https://books.google.com/books?id=4qA2qZhVb9AC&dq=circular+prime&pg=PA330, retrieved 9 March 2011
External links
- Circular prime at The Prime Glossary
- Circular prime at World of Numbers
- OEIS sequence A068652 a related sequence (the circular primes are a subsequence of this one)
- Circular, Permutable, Truncatable and Deletable Primes
 |  |
