Pierpont prime
| Named after | James Pierpont |
|---|---|
| No. of known terms | Thousands |
| Conjectured no. of terms | Infinite |
| Subsequence of | Pierpont number |
| First terms | 2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889 |
| Largest known term | 81 × 220,498,148 + 1 |
| OEIS index | A005109 |
In number theory, a Pierpont prime is a prime number of the form [math]\displaystyle{ 2^u\cdot 3^v + 1\, }[/math] for some nonnegative integers u and v. That is, they are the prime numbers p for which p − 1 is 3-smooth. They are named after the mathematician James Pierpont, who used them to characterize the regular polygons that can be constructed using conic sections. The same characterization applies to polygons that can be constructed using ruler, compass, and angle trisector, or using paper folding.
Except for 2 and the Fermat primes, every Pierpont prime must be 1 modulo 6. The first few Pierpont primes are:
It has been conjectured that there are infinitely many Pierpont primes, but this remains unproven.
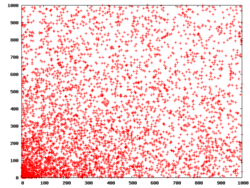
Distribution
| Unsolved problem in mathematics: Are there infinitely many Pierpont primes? (more unsolved problems in mathematics)
|
A Pierpont prime with v = 0 is of the form [math]\displaystyle{ 2^u+1 }[/math], and is therefore a Fermat prime (unless u = 0). If v is positive then u must also be positive (because [math]\displaystyle{ 3^v+1 }[/math] would be an even number greater than 2 and therefore not prime), and therefore the non-Fermat Pierpont primes all have the form 6k + 1, when k is a positive integer (except for 2, when u = v = 0).
Empirically, the Pierpont primes do not seem to be particularly rare or sparsely distributed; there are 42 Pierpont primes less than 106, 65 less than 109, 157 less than 1020, and 795 less than 10100. There are few restrictions from algebraic factorisations on the Pierpont primes, so there are no requirements like the Mersenne prime condition that the exponent must be prime. Thus, it is expected that among n-digit numbers of the correct form [math]\displaystyle{ 2^u\cdot3^v+1 }[/math], the fraction of these that are prime should be proportional to 1/n, a similar proportion as the proportion of prime numbers among all n-digit numbers. As there are [math]\displaystyle{ \Theta(n^{2}) }[/math] numbers of the correct form in this range, there should be [math]\displaystyle{ \Theta(n) }[/math] Pierpont primes.
Andrew M. Gleason made this reasoning explicit, conjecturing there are infinitely many Pierpont primes, and more specifically that there should be approximately 9n Pierpont primes up to 10n.[1] According to Gleason's conjecture there are [math]\displaystyle{ \Theta(\log N) }[/math] Pierpont primes smaller than N, as opposed to the smaller conjectural number [math]\displaystyle{ O(\log \log N) }[/math] of Mersenne primes in that range.
Primality testing
When [math]\displaystyle{ 2^u \gt 3^v }[/math], [math]\displaystyle{ 2^u\cdot 3^v + 1 }[/math] is a Proth number and thus its primality can be tested by Proth's theorem. On the other hand, when [math]\displaystyle{ 2^u \lt 3^v }[/math] alternative primality tests for [math]\displaystyle{ M=2^u\cdot 3^v + 1 }[/math] are possible based on the factorization of [math]\displaystyle{ M-1 }[/math] as a small even number multiplied by a large power of 3.[2]
Pierpont primes found as factors of Fermat numbers
As part of the ongoing worldwide search for factors of Fermat numbers, some Pierpont primes have been announced as factors. The following table[3] gives values of m, k, and n such that
The left-hand side is a Fermat number; the right-hand side is a Pierpont prime.
| m | k | n | Year | Discoverer |
|---|---|---|---|---|
| 38 | 1 | 41 | 1903 | Cullen, Cunningham & Western |
| 63 | 2 | 67 | 1956 | Robinson |
| 207 | 1 | 209 | 1956 | Robinson |
| 452 | 3 | 455 | 1956 | Robinson |
| 9428 | 2 | 9431 | 1983 | Keller |
| 12185 | 4 | 12189 | 1993 | Dubner |
| 28281 | 4 | 28285 | 1996 | Taura |
| 157167 | 1 | 157169 | 1995 | Young |
| 213319 | 1 | 213321 | 1996 | Young |
| 303088 | 1 | 303093 | 1998 | Young |
| 382447 | 1 | 382449 | 1999 | Cosgrave & Gallot |
| 461076 | 1 | 461081 | 2003 | Nohara, Jobling, Woltman & Gallot |
| 495728 | 5 | 495732 | 2007 | Keiser, Jobling, Penné & Fougeron |
| 672005 | 3 | 672007 | 2005 | Cooper, Jobling, Woltman & Gallot |
| 2145351 | 1 | 2145353 | 2003 | Cosgrave, Jobling, Woltman & Gallot |
| 2478782 | 1 | 2478785 | 2003 | Cosgrave, Jobling, Woltman & Gallot |
| 2543548 | 2 | 2543551 | 2011 | Brown, Reynolds, Penné & Fougeron |
(As of 2023), the largest known Pierpont prime is 81 × 220498148 + 1 (6,170,560 decimal digits), whose primality was discovered in June 2023.[4]
Polygon construction
In the mathematics of paper folding, the Huzita axioms define six of the seven types of fold possible. It has been shown that these folds are sufficient to allow the construction of the points that solve any cubic equation.[5] It follows that they allow any regular polygon of N sides to be formed, as long as N ≥ 3 and is of the form 2m3nρ, where ρ is a product of distinct Pierpont primes. This is the same class of regular polygons as those that can be constructed with a compass, straightedge, and angle trisector.[1] Regular polygons which can be constructed with only compass and straightedge (constructible polygons) are the special case where n = 0 and ρ is a product of distinct Fermat primes, themselves a subset of Pierpont primes.
In 1895, James Pierpont studied the same class of regular polygons; his work is what gives the name to the Pierpont primes. Pierpont generalized compass and straightedge constructions in a different way, by adding the ability to draw conic sections whose coefficients come from previously constructed points. As he showed, the regular N-gons that can be constructed with these operations are the ones such that the totient of N is 3-smooth. Since the totient of a prime is formed by subtracting one from it, the primes N for which Pierpont's construction works are exactly the Pierpont primes. However, Pierpont did not describe the form of the composite numbers with 3-smooth totients.[6] As Gleason later showed, these numbers are exactly the ones of the form 2m3nρ given above.[1]
The smallest prime that is not a Pierpont (or Fermat) prime is 11; therefore, the hendecagon is the first regular polygon that cannot be constructed with compass, straightedge and angle trisector (or origami, or conic sections). All other regular N-gons with 3 ≤ N ≤ 21 can be constructed with compass, straightedge and trisector.[1]
Generalization
A Pierpont prime of the second kind is a prime number of the form 2u3v − 1. These numbers are
The largest known primes of this type are Mersenne primes; currently the largest known is [math]\displaystyle{ 2^{82589933}-1 }[/math] (24,862,048 decimal digits). The largest known Pierpont prime of the second kind that is not a Mersenne prime is [math]\displaystyle{ 3\cdot 2^{20928756}-1 }[/math], found by PrimeGrid.[7]
A generalized Pierpont prime is a prime of the form [math]\displaystyle{ p_1^{n_1} \!\cdot p_2^{n_2} \!\cdot p_3^{n_3} \!\cdot \ldots \cdot p_k^{n_k} + 1 }[/math] with k fixed primes p1 < p2 < p3 < ... < pk. A generalized Pierpont prime of the second kind is a prime of the form [math]\displaystyle{ p_1^{n_1} \!\cdot p_2^{n_2} \!\cdot p_3^{n_3} \!\cdot \ldots \cdot p_k^{n_k} - 1 }[/math] with k fixed primes p1 < p2 < p3 < ... < pk. Since all primes greater than 2 are odd, in both kinds p1 must be 2. The sequences of such primes in the OEIS are:
| {p1, p2, p3, ..., pk} | + 1 | − 1 |
| {2} | OEIS: A092506 | OEIS: A000668 |
| {2, 3} | OEIS: A005109 | OEIS: A005105 |
| {2, 5} | OEIS: A077497 | OEIS: A077313 |
| {2, 3, 5} | OEIS: A002200 | OEIS: A293194 |
| {2, 7} | OEIS: A077498 | OEIS: A077314 |
| {2, 3, 5, 7} | OEIS: A174144 | OEIS: A347977 |
| {2, 11} | OEIS: A077499 | OEIS: A077315 |
| {2, 13} | OEIS: A173236 | OEIS: A173062 |
See also
- Proth prime, the primes of the form [math]\displaystyle{ N = k \cdot 2^n + 1 }[/math] where k and n are positive integers, [math]\displaystyle{ k }[/math] is odd and [math]\displaystyle{ 2^n \gt k. }[/math]
References
- ↑ 1.0 1.1 1.2 1.3 "Angle trisection, the heptagon, and the triskaidecagon", American Mathematical Monthly 95 (3): 185–194, 1988, doi:10.2307/2323624. Footnote 8, p. 191.
- ↑ Kirfel, Christoph; Rødseth, Øystein J. (2001), "On the primality of [math]\displaystyle{ 2h\cdot 3^n+1 }[/math]", Discrete Mathematics 241 (1-3): 395–406, doi:10.1016/S0012-365X(01)00125-X.
- ↑ Wilfrid Keller, Fermat factoring status.
- ↑ Caldwell, Chris, The largest known primes, http://primes.utm.edu/primes/lists/short.txt, retrieved 17 June 2023; The Prime Database: 81*2^20498148+1, https://primes.utm.edu/primes/page.php?id=136165, retrieved 17 June 2023
- ↑ "Solving cubics with creases: the work of Beloch and Lill", American Mathematical Monthly 118 (4): 307–315, 2011, doi:10.4169/amer.math.monthly.118.04.307.
- ↑ "On an undemonstrated theorem of the Disquisitiones Arithmeticæ", Bulletin of the American Mathematical Society 2 (3): 77–83, 1895, doi:10.1090/S0002-9904-1895-00317-1.
- ↑ 3*2^20928756 - 1 (6,300,184 Decimal Digits), from The Prime Pages.
 |