Pythagorean prime

The Pythagorean prime 5 and its square root are both hypotenuses of right triangles with integer legs. The formulas show how to transform any right triangle with integer legs into another right triangle with integer legs whose hypotenuse is the square of the first triangle's hypotenuse.

A Pythagorean prime is a prime number of the form [math]\displaystyle{ 4n+1 }[/math]. Pythagorean primes are exactly the odd prime numbers that are the sum of two squares; this characterization is Fermat's theorem on sums of two squares.

Equivalently, by the Pythagorean theorem, they are the odd prime numbers [math]\displaystyle{ p }[/math] for which [math]\displaystyle{ \sqrt p }[/math] is the length of the hypotenuse of a right triangle with integer legs, and they are also the prime numbers [math]\displaystyle{ p }[/math] for which [math]\displaystyle{ p }[/math] itself is the hypotenuse of a primitive Pythagorean triangle. For instance, the number 5 is a Pythagorean prime; [math]\displaystyle{ \sqrt5 }[/math] is the hypotenuse of a right triangle with legs 1 and 2, and 5 itself is the hypotenuse of a right triangle with legs 3 and 4.

Values and density

The first few Pythagorean primes are

5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, ... (sequence A002144 in the OEIS).

By Dirichlet's theorem on arithmetic progressions, this sequence is infinite. More strongly, for each [math]\displaystyle{ n }[/math], the numbers of Pythagorean and non-Pythagorean primes up to [math]\displaystyle{ n }[/math] are approximately equal. However, the number of Pythagorean primes up to [math]\displaystyle{ n }[/math] is frequently somewhat smaller than the number of non-Pythagorean primes; this phenomenon is known as Chebyshev's bias. For example, the only values of [math]\displaystyle{ n }[/math] up to 600000 for which there are more Pythagorean than non-Pythagorean odd primes less than or equal to n are 26861 and 26862.

Representation as a sum of two squares

The sum of one odd square and one even square is congruent to 1 mod 4, but there exist composite numbers such as 21 that are 1 mod 4 and yet cannot be represented as sums of two squares. Fermat's theorem on sums of two squares states that the prime numbers that can be represented as sums of two squares are exactly 2 and the odd primes congruent to 1 mod 4. The representation of each such number is unique, up to the ordering of the two squares.

By using the Pythagorean theorem, this representation can be interpreted geometrically: the Pythagorean primes are exactly the odd prime numbers [math]\displaystyle{ p }[/math] such that there exists a right triangle, with integer legs, whose hypotenuse has length [math]\displaystyle{ \sqrt p }[/math]. They are also exactly the prime numbers [math]\displaystyle{ p }[/math] such that there exists a right triangle with integer sides whose hypotenuse has length [math]\displaystyle{ p }[/math]. For, if the triangle with legs [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] has hypotenuse length [math]\displaystyle{ \sqrt p }[/math] (with [math]\displaystyle{ x\gt y }[/math]), then the triangle with legs [math]\displaystyle{ x^2-y^2 }[/math] and [math]\displaystyle{ 2xy }[/math] has hypotenuse length [math]\displaystyle{ p }[/math].

Another way to understand this representation as a sum of two squares involves Gaussian integers, the complex numbers whose real part and imaginary part are both integers. The norm of a Gaussian integer [math]\displaystyle{ x+iy }[/math] is the number [math]\displaystyle{ x^2+y^2 }[/math]. Thus, the Pythagorean primes (and 2) occur as norms of Gaussian integers, while other primes do not. Within the Gaussian integers, the Pythagorean primes are not considered to be prime numbers, because they can be factored as [math]\displaystyle{ p=(x+iy)(x-iy). }[/math] Similarly, their squares can be factored in a different way than their integer factorization, as [math]\displaystyle{ \begin{align} p^2&=(x+iy)^2(x-iy)^2\\ &=(x^2-y^2+2ixy)(x^2-y^2-2ixy).\\ \end{align} }[/math] The real and imaginary parts of the factors in these factorizations are the leg lengths of the right triangles having the given hypotenuses.

Quadratic residues

The law of quadratic reciprocity says that if [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] are distinct odd primes, at least one of which is Pythagorean, then [math]\displaystyle{ p }[/math] is a quadratic residue mod [math]\displaystyle{ q }[/math] if and only if [math]\displaystyle{ q }[/math] is a quadratic residue mod [math]\displaystyle{ p }[/math]; by contrast, if neither [math]\displaystyle{ p }[/math] nor [math]\displaystyle{ q }[/math] is Pythagorean, then [math]\displaystyle{ p }[/math] is a quadratic residue mod [math]\displaystyle{ q }[/math] if and only if [math]\displaystyle{ q }[/math] is not a quadratic residue mod [math]\displaystyle{ p }[/math].

In the finite field [math]\displaystyle{ \Z/p }[/math] with [math]\displaystyle{ p }[/math] a Pythagorean prime, the polynomial equation [math]\displaystyle{ x^2=-1 }[/math] has two solutions. This may be expressed by saying that [math]\displaystyle{ -1 }[/math] is a quadratic residue mod [math]\displaystyle{ p }[/math]. In contrast, this equation has no solution in the finite fields [math]\displaystyle{ \Z/p }[/math] where [math]\displaystyle{ p }[/math] is an odd prime but is not Pythagorean.

The Paley graph with 13 vertices

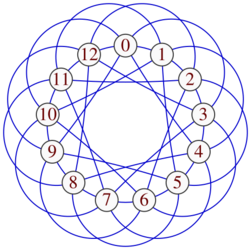
For every Pythagorean prime [math]\displaystyle{ p }[/math], there exists a Paley graph with [math]\displaystyle{ p }[/math] vertices, representing the numbers modulo [math]\displaystyle{ p }[/math], with two numbers adjacent in the graph if and only if their difference is a quadratic residue. This definition produces the same adjacency relation regardless of the order in which the two numbers are subtracted to compute their difference, because of the property of Pythagorean primes that [math]\displaystyle{ -1 }[/math] is a quadratic residue.

External links

• Eaves, Laurence, "Pythagorean Primes: including 5, 13 and 137", Numberphile (Brady Haran), http://www.numberphile.com/videos/pythagorean_primes.html, retrieved 2013-04-02 
• OEIS sequence A007350 (Where prime race 4n-1 vs. 4n+1 changes leader)