Motzkin number

Motzkin number

Named after	Theodore Motzkin
Publication year	1948
Author of publication	Theodore Motzkin
No. of known terms	infinity
Formula	see Properties
First terms	1, 1, 2, 4, 9, 21, 51
OEIS index	A001006 Motzkin

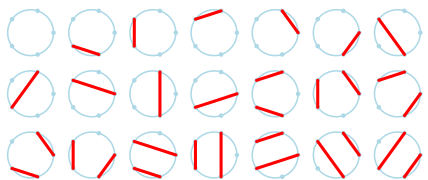
In mathematics, the nth Motzkin number is the number of different ways of drawing non-intersecting chords between n points on a circle (not necessarily touching every point by a chord). The Motzkin numbers are named after Theodore Motzkin and have diverse applications in geometry, combinatorics and number theory.

The Motzkin numbers [math]\displaystyle{ M_n }[/math] for [math]\displaystyle{ n = 0, 1, \dots }[/math] form the sequence:

1, 1, 2, 4, 9, 21, 51, 127, 323, 835, ... (sequence A001006 in the OEIS)

Examples

The following figure shows the 9 ways to draw non-intersecting chords between 4 points on a circle (M₄ = 9):

The following figure shows the 21 ways to draw non-intersecting chords between 5 points on a circle (M₅ = 21):

Properties

The Motzkin numbers satisfy the recurrence relations

[math]\displaystyle{ M_{n}=M_{n-1}+\sum_{i=0}^{n-2}M_iM_{n-2-i}=\frac{2n+1}{n+2}M_{n-1}+\frac{3n-3}{n+2}M_{n-2}. }[/math]

The Motzkin numbers can be expressed in terms of binomial coefficients and Catalan numbers:

[math]\displaystyle{ M_n=\sum_{k=0}^{\lfloor n/2\rfloor} \binom{n}{2k} C_k, }[/math]

and inversely,

[math]\displaystyle{ C_{n+1}=\sum_{k=0}^{n} \binom{n}{k} M_k }[/math]

This gives

[math]\displaystyle{ \sum_{k=0}^{n}C_{k} = 1 + \sum_{k=1}^{n} \binom{n}{k} M_{k-1}. }[/math]

The generating function [math]\displaystyle{ m(x) = \sum_{n=0}^\infty M_n x^n }[/math] of the Motzkin numbers satisfies

[math]\displaystyle{ x^2 m(x)^2 + (x - 1) m(x) + 1 = 0 }[/math]

and is explicitly expressed as

[math]\displaystyle{ m(x) = \frac{1-x-\sqrt{1-2x-3x^2}}{2x^2}. }[/math]

An integral representation of Motzkin numbers is given by

[math]\displaystyle{ M_{n}=\frac{2}{\pi}\int_0^\pi \sin(x)^2(2\cos(x)+1)^n dx }[/math].

They have the asymptotic behaviour

[math]\displaystyle{ M_{n}\sim \frac{1}{2 \sqrt{\pi}}\left(\frac{3}{n}\right)^{3/2} 3^n,~ n \to \infty }[/math].

A Motzkin prime is a Motzkin number that is prime. (As of 2019), only four such primes are known:

2, 127, 15511, 953467954114363 (sequence A092832 in the OEIS)

Combinatorial interpretations

The Motzkin number for n is also the number of positive integer sequences of length n − 1 in which the opening and ending elements are either 1 or 2, and the difference between any two consecutive elements is −1, 0 or 1. Equivalently, the Motzkin number for n is the number of positive integer sequences of length n + 1 in which the opening and ending elements are 1, and the difference between any two consecutive elements is −1, 0 or 1.

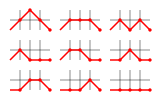
Also, the Motzkin number for n gives the number of routes on the upper right quadrant of a grid from coordinate (0, 0) to coordinate (n, 0) in n steps if one is allowed to move only to the right (up, down or straight) at each step but forbidden from dipping below the y = 0 axis.

For example, the following figure shows the 9 valid Motzkin paths from (0, 0) to (4, 0):

There are at least fourteen different manifestations of Motzkin numbers in different branches of mathematics, as enumerated by (Donaghey Shapiro) in their survey of Motzkin numbers. (Guibert Pergola) showed that vexillary involutions are enumerated by Motzkin numbers.

See also

• Telephone number which represent the number of ways of drawing chords if intersections are allowed
• Delannoy number
• Narayana number
• Schröder number

References

• Bernhart, Frank R. (1999), "Catalan, Motzkin, and Riordan numbers", Discrete Mathematics 204 (1–3): 73–112, doi:10.1016/S0012-365X(99)00054-0 
• Donaghey, R.; Shapiro, L. W. (1977), "Motzkin numbers", Journal of Combinatorial Theory, Series A 23 (3): 291–301, doi:10.1016/0097-3165(77)90020-6 
• Guibert, O.; Pergola, E.; Pinzani, R. (2001), "Vexillary involutions are enumerated by Motzkin numbers", Annals of Combinatorics 5 (2): 153–174, doi:10.1007/PL00001297, ISSN 0218-0006 
• Motzkin (1948), "Relations between hypersurface cross ratios, and a combinatorial formula for partitions of a polygon, for permanent preponderance, and for non-associative products", Bulletin of the American Mathematical Society 54 (4): 352–360, doi:10.1090/S0002-9904-1948-09002-4 

External links

• Weisstein, Eric W.. "Motzkin Number". http://mathworld.wolfram.com/MotzkinNumber.html.