Graph neural network

From HandWiki
Short description: Class of artificial neural networks
Machine learning and
data mining
Kernel Machine.svg
Problems
Supervised learning
(classification • regression)
Clustering
Dimensionality reduction
Structured prediction
Anomaly detection
Artificial neural networks
Reinforcement learning
Theory
Machine-learning venues
Glossary of artificial intelligence
Related articles

A graph neural network (GNN) belongs to a class of artificial neural networks for processing data that can be represented as graphs.[1][2][3][4][5]

Basic building blocks of a graph neural network (GNN). [math]\displaystyle{ (1) }[/math] Permutation equivariant layer. [math]\displaystyle{ (2) }[/math] Local pooling layer. [math]\displaystyle{ (3) }[/math] Global pooling (or readout) layer. Colors indicate features.

In the more general subject of "geometric deep learning", certain existing neural network architectures can be interpreted as GNNs operating on suitably defined graphs.[6] A convolutional neural network layer, in the context of computer vision, can be seen as a GNN applied to graphs whose nodes are pixels and only adjacent pixels are connected by edges in the graph. A transformer layer, in natural language processing, can be seen as a GNN applied to complete graphs whose nodes are words or tokens in a passage of natural language text.

The key design element of GNNs is the use of pairwise message passing, such that graph nodes iteratively update their representations by exchanging information with their neighbors. Since their inception, several different GNN architectures have been proposed,[2][3][7][8][9] which implement different flavors of message passing,[6] started by recursive[2] or convolutional constructive[3] approaches. (As of 2022), whether it is possible to define GNN architectures "going beyond" message passing, or if every GNN can be built on message passing over suitably defined graphs, is an open research question.[10]

Relevant application domains for GNNs include Natural Language Processing, [11] social networks,[12] citation networks,[13] molecular biology,[14] chemistry,[15][16] physics[17] and NP-hard combinatorial optimization problems.[18]

Several open source libraries implementing graph neural networks are available, such as PyTorch Geometric[19] (PyTorch), TensorFlow GNN[20] (TensorFlow), jraph[21] (Google JAX), and GraphNeuralNetworks.jl[22] (Julia, Flux).

Architecture

The architecture of a generic GNN implements the following fundamental layers:[6]

  1. Permutation equivariant: a permutation equivariant layer maps a representation of a graph into an updated representation of the same graph. In the literature, permutation equivariant layers are implemented via pairwise message passing between graph nodes.[6][10] Intuitively, in a message passing layer, nodes update their representations by aggregating the messages received from their immediate neighbours. As such, each message passing layer increases the receptive field of the GNN by one hop.
  2. Local pooling: a local pooling layer coarsens the graph via downsampling. Local pooling is used to increase the receptive field of a GNN, in a similar fashion to pooling layers in convolutional neural networks. Examples include k-nearest neighbours pooling, top-k pooling,[23] and self-attention pooling.[24]
  3. Global pooling: a global pooling layer, also known as readout layer, provides fixed-size representation of the whole graph. The global pooling layer must be permutation invariant, such that permutations in the ordering of graph nodes and edges do not alter the final output.[25] Examples include element-wise sum, mean or maximum.

It has been demonstrated that GNNs cannot be more expressive than the Weisfeiler–Leman Graph Isomorphism Test.[26][27] In practice, this means that there exist different graph structures (e.g., molecules with the same atoms but different bonds) that cannot be distinguished by GNNs. More powerful GNNs operating on higher-dimension geometries such as simplicial complexes can be designed.[28][29] (As of 2022), whether or not future architectures will overcome the message passing primitive is an open research question.[10]

Non-isomorphic graphs that cannot be distinguished by a GNN due to the limitations of the Weisfeiler-Lehman Graph Isomorphism Test. Colors indicate node features.

Message passing layers

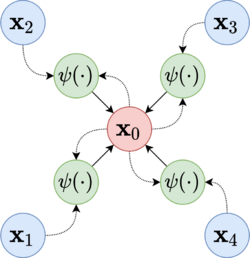
Node representation update in a Message Passing Neural Network (MPNN) layer. Node [math]\displaystyle{ \mathbf{x}_0 }[/math] receives messages sent by all of its immediate neighbours [math]\displaystyle{ \mathbf{x}_1 }[/math] to [math]\displaystyle{ \mathbf{x}_4 }[/math]. Messages are computing via the message function [math]\displaystyle{ \phi }[/math], which accounts for the features of both senders and receiver.

Message passing layers are permutation-equivariant layers mapping a graph into an updated representation of the same graph. Formally, they can be expressed as message passing neural networks (MPNNs).[6]

Let [math]\displaystyle{ G = (V,E) }[/math] be a graph, where [math]\displaystyle{ V }[/math] is the node set and [math]\displaystyle{ E }[/math] is the edge set. Let [math]\displaystyle{ N_u }[/math] be the neighbourhood of some node [math]\displaystyle{ u \in V }[/math]. Additionally, let [math]\displaystyle{ \mathbf{x}_u }[/math] be the features of node [math]\displaystyle{ u \in V }[/math], and [math]\displaystyle{ \mathbf{e}_{uv} }[/math] be the features of edge [math]\displaystyle{ (u, v) \in E }[/math]. An MPNN layer can be expressed as follows:[6]

[math]\displaystyle{ \mathbf{h}_u = \phi \left( \mathbf{x}_u, \bigoplus_{v \in N_u} \psi(\mathbf{x}_u, \mathbf{x}_v, \mathbf{e}_{uv}) \right) }[/math]

where [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \psi }[/math] are differentiable functions (e.g., artificial neural networks), and [math]\displaystyle{ \bigoplus }[/math] is a permutation invariant aggregation operator that can accept an arbitrary number of inputs (e.g., element-wise sum, mean, or max). In particular, [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \psi }[/math] are referred to as update and message functions, respectively. Intuitively, in an MPNN computational block, graph nodes update their representations by aggregating the messages received from their neighbours.

The outputs of one or more MPNN layers are node representations [math]\displaystyle{ \mathbf{h}_u }[/math] for each node [math]\displaystyle{ u \in V }[/math] in the graph. Node representations can be employed for any downstream task, such as node/graph classification or edge prediction.

Graph nodes in an MPNN update their representation aggregating information from their immediate neighbours. As such, stacking [math]\displaystyle{ n }[/math] MPNN layers means that one node will be able to communicate with nodes that are at most [math]\displaystyle{ n }[/math] "hops" away. In principle, to ensure that every node receives information from every other node, one would need to stack a number of MPNN layers equal to the graph diameter. However, stacking many MPNN layers may cause issues such as oversmoothing[30] and oversquashing.[31] Oversmoothing refers to the issue of node representations becoming indistinguishable. Oversquashing refers to the bottleneck that is created by squeezing long-range dependencies into fixed-size representations. Countermeasures such as skip connections[8][32] (as in residual neural networks), gated update rules[33] and jumping knowledge[34] can mitigate oversmoothing. Modifying the final layer to be a fully-adjacent layer, i.e., by considering the graph as a complete graph, can mitigate oversquashing in problems where long-range dependencies are required.[31]

Other "flavours" of MPNN have been developed in the literature,[6] such as graph convolutional networks[7] and graph attention networks,[9] whose definitions can be expressed in terms of the MPNN formalism.

Graph convolutional network

The graph convolutional network (GCN) was first introduced by Thomas Kipf and Max Welling in 2017.[7]

A GCN layer defines a first-order approximation of a localized spectral filter on graphs. GCNs can be understood as a generalization of convolutional neural networks to graph-structured data.

The formal expression of a GCN layer reads as follows:

[math]\displaystyle{ \mathbf{H} = \sigma\left(\tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{X} \mathbf{\Theta}\right) }[/math]

where [math]\displaystyle{ \mathbf{H} }[/math] is the matrix of node representations [math]\displaystyle{ \mathbf{h}_u }[/math], [math]\displaystyle{ \mathbf{X} }[/math] is the matrix of node features [math]\displaystyle{ \mathbf{x}_u }[/math], [math]\displaystyle{ \sigma(\cdot) }[/math] is an activation function (e.g., ReLU), [math]\displaystyle{ \tilde{\mathbf{A}} }[/math] is the graph adjacency matrix with the addition of self-loops, [math]\displaystyle{ \tilde{\mathbf{D}} }[/math] is the graph degree matrix with the addition of self-loops, and [math]\displaystyle{ \mathbf{\Theta} }[/math] is a matrix of trainable parameters.

In particular, let [math]\displaystyle{ \mathbf{A} }[/math] be the graph adjacency matrix: then, one can define [math]\displaystyle{ \tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I} }[/math] and [math]\displaystyle{ \tilde{\mathbf{D}}_{ii} = \sum_{j \in V} \tilde{A}_{ij} }[/math], where [math]\displaystyle{ \mathbf{I} }[/math] denotes the identity matrix. This normalization ensures that the eigenvalues of [math]\displaystyle{ \tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} }[/math] are bounded in the range [math]\displaystyle{ [0, 1] }[/math], avoiding numerical instabilities and exploding/vanishing gradients.

A limitation of GCNs is that they do not allow multidimensional edge features [math]\displaystyle{ \mathbf{e}_{uv} }[/math].[7] It is however possible to associate scalar weights [math]\displaystyle{ w_{uv} }[/math] to each edge by imposing [math]\displaystyle{ A_{uv} = w_{uv} }[/math], i.e., by setting each nonzero entry in the adjacency matrix equal to the weight of the corresponding edge.

Graph attention network

The graph attention network (GAT) was introduced by Petar Veličković et al. in 2018.[9]

Graph attention network is a combination of a graph neural network and an attention layer. The implementation of attention layer in graphical neural networks helps provide attention or focus to the important information from the data instead of focusing on the whole data.

A multi-head GAT layer can be expressed as follows:

[math]\displaystyle{ \mathbf{h}_u = \overset{K}{\underset{k=1}{\Big\Vert}} \sigma \left(\sum_{v \in N_u} \alpha_{uv} \mathbf{W}^k \mathbf{x}_v\right) }[/math]

where [math]\displaystyle{ K }[/math] is the number of attention heads, [math]\displaystyle{ \Big\Vert }[/math] denotes vector concatenation, [math]\displaystyle{ \sigma(\cdot) }[/math] is an activation function (e.g., ReLU), [math]\displaystyle{ \alpha_{ij} }[/math] are attention coefficients, and [math]\displaystyle{ W^k }[/math] is a matrix of trainable parameters for the [math]\displaystyle{ k }[/math]-th attention head.

For the final GAT layer, the outputs from each attention head are averaged before the application of the activation function. Formally, the final GAT layer can be written as:

[math]\displaystyle{ \mathbf{h}_u = \sigma \left(\frac{1}{K}\sum_{k=1}^K \sum_{v \in N_u} \alpha_{uv} \mathbf{W}^k \mathbf{x}_v\right) }[/math]

Attention in Machine Learning is a technique that mimics cognitive attention. In the context of learning on graphs, the attention coefficient [math]\displaystyle{ \alpha_{uv} }[/math] measures how important is node [math]\displaystyle{ u \in V }[/math] to node [math]\displaystyle{ v \in V }[/math].

Normalized attention coefficients are computed as follows:

[math]\displaystyle{ \alpha_{uv} = \frac{\exp(\text{LeakyReLU}\left(\mathbf{a}^T [\mathbf{W} \mathbf{h}_u \Vert \mathbf{W} \mathbf{h}_v \Vert \mathbf{e}_{uv}]\right))}{\sum_{z \in N_u}\exp(\text{LeakyReLU}\left(\mathbf{a}^T [\mathbf{W} \mathbf{h}_u \Vert \mathbf{W} \mathbf{h}_z \Vert \mathbf{e}_{uz}]\right))} }[/math]

where [math]\displaystyle{ \mathbf{a} }[/math] is a vector of learnable weights, [math]\displaystyle{ \cdot^T }[/math] indicates transposition, and [math]\displaystyle{ \text{LeakyReLU} }[/math] is a modified ReLU activation function. Attention coefficients are normalized to make them easily comparable across different nodes.[9]

A GCN can be seen as a special case of a GAT where attention coefficients are not learnable, but fixed and equal to the edge weights [math]\displaystyle{ w_{uv} }[/math].

Gated graph sequence neural network

The gated graph sequence neural network (GGS-NN) was introduced by Yujia Li et al. in 2015.[33] The GGS-NN extends the GNN formulation by Scarselli et al.[2] to output sequences. The message passing framework is implemented as an update rule to a gated recurrent unit (GRU) cell.

A GGS-NN can be expressed as follows:

[math]\displaystyle{ \mathbf{h}_u^{(0)} = \mathbf{x}_u \, \Vert \, \mathbf{0} }[/math]
[math]\displaystyle{ \mathbf{m}_u^{(l+1)} = \sum_{v \in N_u} \mathbf{\Theta} \mathbf{h}_v }[/math]
[math]\displaystyle{ \mathbf{h}_u^{(l+1)} = \text{GRU}(\mathbf{m}_u^{(l+1)}, \mathbf{h}_u^{(l)}) }[/math]

where [math]\displaystyle{ \Vert }[/math] denotes vector concatenation, [math]\displaystyle{ \mathbf{0} }[/math] is a vector of zeros, [math]\displaystyle{ \mathbf{\Theta} }[/math] is a matrix of learnable parameters, [math]\displaystyle{ \text{GRU} }[/math] is a GRU cell, and [math]\displaystyle{ l }[/math] denotes the sequence index. In a GGS-NN, the node representations are regarded as the hidden states of a GRU cell. The initial node features [math]\displaystyle{ \mathbf{x}_u^{(0)} }[/math] are zero-padded up to the hidden state dimension of the GRU cell. The same GRU cell is used for updating representations for each node.

Local pooling layers

Local pooling layers coarsen the graph via downsampling. We present here several learnable local pooling strategies that have been proposed.[25] For each cases, the input is the initial graph is represented by a matrix [math]\displaystyle{ \mathbf{X} }[/math] of node features, and the graph adjacency matrix [math]\displaystyle{ \mathbf{A} }[/math]. The output is the new matrix [math]\displaystyle{ \mathbf{X}' }[/math]of node features, and the new graph adjacency matrix [math]\displaystyle{ \mathbf{A}' }[/math].

Top-k pooling

We first set

[math]\displaystyle{ \mathbf{y} = \frac{\mathbf{X}\mathbf{p}}{\Vert\mathbf{p}\Vert} }[/math]

where [math]\displaystyle{ \mathbf{p} }[/math] is a learnable projection vector. The projection vector [math]\displaystyle{ \mathbf{p} }[/math] computes a scalar projection value for each graph node.

The top-k pooling layer [23] can then be formalised as follows:

[math]\displaystyle{ \mathbf{X}' = (\mathbf{X} \odot \text{sigmoid}(\mathbf{y}))_{\mathbf{i}} }[/math]
[math]\displaystyle{ \mathbf{A}' = \mathbf{A}_{\mathbf{i}, \mathbf{i}} }[/math]

where [math]\displaystyle{ \mathbf{i} = \text{top}_k(\mathbf{y}) }[/math] is the subset of nodes with the top-k highest projection scores, [math]\displaystyle{ \odot }[/math] denotes element-wise matrix multiplication, and [math]\displaystyle{ \text{sigmoid}(\cdot) }[/math] is the sigmoid function. In other words, the nodes with the top-k highest projection scores are retained in the new adjacency matrix [math]\displaystyle{ \mathbf{A}' }[/math]. The [math]\displaystyle{ \text{sigmoid}(\cdot) }[/math] operation makes the projection vector [math]\displaystyle{ \mathbf{p} }[/math] trainable by backpropagation, which otherwise would produce discrete outputs.[23]

Self-attention pooling

We first set

[math]\displaystyle{ \mathbf{y} = \text{GNN}(\mathbf{X}, \mathbf{A}) }[/math]

where [math]\displaystyle{ \text{GNN} }[/math] is a generic permutation equivariant GNN layer (e.g., GCN, GAT, MPNN).

The Self-attention pooling layer[24] can then be formalised as follows:

[math]\displaystyle{ \mathbf{X}' = (\mathbf{X} \odot \mathbf{y})_{\mathbf{i}} }[/math]
[math]\displaystyle{ \mathbf{A}' = \mathbf{A}_{\mathbf{i}, \mathbf{i}} }[/math]

where [math]\displaystyle{ \mathbf{i} = \text{top}_k(\mathbf{y}) }[/math] is the subset of nodes with the top-k highest projection scores, [math]\displaystyle{ \odot }[/math] denotes element-wise matrix multiplication.

The self-attention pooling layer can be seen as an extension of the top-k pooling layer. Differently from top-k pooling, the self-attention scores computed in self-attention pooling account both for the graph features and the graph topology.

Applications

Protein folding

Graph neural networks are one of the main building blocks of AlphaFold, an artificial intelligence program developed by Google's DeepMind for solving the protein folding problem in biology. AlphaFold achieved first place in several CASP competitions.[35][36][34]

Social networks

Social networks are a major application domain for GNNs due to their natural representation as social graphs. GNNs are used to develop recommender systems based on both social relations and item relations.[37][12]

Combinatorial optimization

GNNs are used as fundamental building blocks for several combinatorial optimization algorithms.[38] Examples include computing shortest paths or Eulerian circuits for a given graph,[33] deriving chip placements superior or competitive to handcrafted human solutions,[39] and improving expert-designed branching rules in branch and bound.[40]

Cyber security

When viewed as a graph, a network of computers can be analyzed with GNNs for anomaly detection. Anomalies within provenance graphs often correlate to malicious activity within the network. GNNs have been used to identify these anomalies on individual nodes[41] and within paths[42] to detect malicious processes, or on the edge level[43] to detect lateral movement.

References

  1. ↑ Wu, Lingfei; Cui, Peng; Pei, Jian; Zhao, Liang (2022). "Graph Neural Networks: Foundations, Frontiers, and Applications". Springer Singapore: 725. https://graph-neural-networks.github.io/. 
  2. ↑ 2.0 2.1 2.2 2.3 Scarselli, Franco; Gori, Marco; Tsoi, Ah Chung; Hagenbuchner, Markus; Monfardini, Gabriele (2009). "The Graph Neural Network Model". IEEE Transactions on Neural Networks 20 (1): 61–80. doi:10.1109/TNN.2008.2005605. ISSN 1941-0093. PMID 19068426. https://ieeexplore.ieee.org/document/4700287. 
  3. ↑ 3.0 3.1 3.2 Micheli, Alessio (2009). "Neural Network for Graphs: A Contextual Constructive Approach". IEEE Transactions on Neural Networks 20 (3): 498–511. doi:10.1109/TNN.2008.2010350. ISSN 1045-9227. PMID 19193509. https://ieeexplore.ieee.org/document/4700287. 
  4. ↑ Sanchez-Lengeling, Benjamin; Reif, Emily; Pearce, Adam; Wiltschko, Alex (2021-09-02). "A Gentle Introduction to Graph Neural Networks". Distill 6 (9): e33. doi:10.23915/distill.00033. ISSN 2476-0757. https://distill.pub/2021/gnn-intro. 
  5. ↑ Daigavane, Ameya; Ravindran, Balaraman; Aggarwal, Gaurav (2021-09-02). "Understanding Convolutions on Graphs". Distill 6 (9): e32. doi:10.23915/distill.00032. ISSN 2476-0757. https://distill.pub/2021/understanding-gnns. 
  6. ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Bronstein, Michael M.; Bruna, Joan; Cohen, Taco; Veličković, Petar (May 4, 2021). "Geometric Deep Learning: Grids, Groups, Graphs Geodesics and Gauges". arXiv:2104.13478 [cs.LG].
  7. ↑ 7.0 7.1 7.2 7.3 Kipf, Thomas N; Welling, Max (2016). "Semi-supervised classification with graph convolutional networks". IEEE Transactions on Neural Networks 5 (1): 61–80. doi:10.1109/TNN.2008.2005605. PMID 19068426. https://ieeexplore.ieee.org/document/4700287. 
  8. ↑ 8.0 8.1 Hamilton, William; Ying, Rex; Leskovec, Jure (2017). "Inductive Representation Learning on Large Graphs". Neural Information Processing Systems 31. https://cs.stanford.edu/people/jure/pubs/graphsage-nips17.pdf. 
  9. ↑ 9.0 9.1 9.2 9.3 Veličković, Petar; Cucurull, Guillem; Casanova, Arantxa; Romero, Adriana; Liò, Pietro; Bengio, Yoshua (2018-02-04). "Graph Attention Networks". arXiv:1710.10903 [stat.ML].
  10. ↑ 10.0 10.1 10.2 Veličković, Petar (2022). "Message passing all the way up". arXiv:2202.11097 [cs.LG].
  11. ↑ Wu, Lingfei; Chen, Yu; Shen, Kai; Guo, Xiaojie; Gao, Hanning; Li, Shucheng; Pei, Jian; Long, Bo (2023). "Graph Neural Networks for Natural Language Processing: A Survey". Foundations and Trends in Machine Learning 16 (2): 119–328. doi:10.1561/2200000096. ISSN 1941-0093. PMID 19068426. https://www.nowpublishers.com/article/Details/MAL-096. 
  12. ↑ 12.0 12.1 Ying, Rex; He, Ruining; Chen, Kaifeng; Eksombatchai, Pong; Hamilton, William L.; Leskovec, Jure (2018). Graph Convolutional Neural Networks for Web-Scale Recommender Systems. pp. 974–983. doi:10.1145/3219819.3219890. ISBN 9781450355520. 
  13. ↑ "Stanford Large Network Dataset Collection". https://snap.stanford.edu/data/. 
  14. ↑ Zhang, Weihang; Cui, Yang; Liu, Bowen; Loza, Martin; Park, Sung-Joon; Nakai, Kenta (1 December 2023). HyGAnno: Hybrid graph neural network-based cell type annotation for single-cell ATAC sequencing data. doi:10.1101/2023.11.29.569114. 
  15. ↑ Gilmer, Justin; Schoenholz, Samuel S.; Riley, Patrick F.; Vinyals, Oriol; Dahl, George E. (2017-07-17). "Neural Message Passing for Quantum Chemistry" (in en). Proceedings of Machine Learning Research: 1263–1272. http://proceedings.mlr.press/v70/gilmer17a.html. 
  16. ↑ Coley, Connor W.; Jin, Wengong; Rogers, Luke; Jamison, Timothy F.; Jaakkola, Tommi S.; Green, William H.; Barzilay, Regina; Jensen, Klavs F. (2019-01-02). "A graph-convolutional neural network model for the prediction of chemical reactivity" (in en). Chemical Science 10 (2): 370–377. doi:10.1039/C8SC04228D. ISSN 2041-6539. PMID 30746086. 
  17. ↑ Qasim, Shah Rukh; Kieseler, Jan; Iiyama, Yutaro; Pierini, Maurizio Pierini (2019). "Learning representations of irregular particle-detector geometry with distance-weighted graph networks". The European Physical Journal C 79 (7). doi:10.1140/epjc/s10052-019-7113-9. 
  18. ↑ Li, Zhuwen; Chen, Qifeng; Koltun, Vladlen (2018). "Combinatorial optimization with graph convolutional networks and guided tree search". Neural Information Processing Systems 31: 537–546. 
  19. ↑ Matthias, Fey; Lenssen, Jan E. (2019). "Fast Graph Representation Learning with PyTorch Geometric". arXiv:1903.02428 [cs.LG].
  20. ↑ "Tensorflow GNN". https://github.com/tensorflow/gnn. 
  21. ↑ "jraph". https://github.com/deepmind/jraph. 
  22. ↑ Lucibello, Carlo (2021). "GraphNeuralNetworks.jl". https://github.com/CarloLucibello/GraphNeuralNetworks.jl. 
  23. ↑ 23.0 23.1 23.2 Gao, Hongyang; Ji, Shuiwang Ji (2019). "Graph U-Nets". arXiv:1905.05178 [cs.LG].
  24. ↑ 24.0 24.1 Lee, Junhyun; Lee, Inyeop; Kang, Jaewoo (2019). "Self-Attention Graph Pooling". arXiv:1904.08082 [cs.LG].
  25. ↑ 25.0 25.1 Liu, Chuang; Zhan, Yibing; Li, Chang; Du, Bo; Wu, Jia; Hu, Wenbin; Liu, Tongliang; Tao, Dacheng (2022). "Graph Pooling for Graph Neural Networks: Progress, Challenges, and Opportunities". arXiv:2204.07321 [cs.LG].
  26. ↑ Douglas, B. L. (2011-01-27). "The Weisfeiler–Lehman Method and Graph Isomorphism Testing". arXiv:1101.5211 [math.CO].
  27. ↑ Xu, Keyulu; Hu, Weihua; Leskovec, Jure; Jegelka, Stefanie (2019-02-22). "How Powerful are Graph Neural Networks?". arXiv:1810.00826 [cs.LG].
  28. ↑ Bodnar, Christian; Frasca, Fabrizio; Guang Wang, Yu; Otter, Nina; Montúfar, Guido; Liò, Pietro; Bronstein, Michael (2021). "Weisfeiler and Lehman Go Topological: Message Passing Simplicial Networks". arXiv:2103.03212 [cs.LG].
  29. ↑ Grady, Leo; Polimeni, Jonathan (2011). Discrete Calculus: Applied Analysis on Graphs for Computational Science. Springer. http://leogrady.net/wp-content/uploads/2017/01/grady2010discrete.pdf. 
  30. ↑ Chen, Deli; Lin, Yankai; Li, Wei; Li, Peng; Zhou, Jie; Sun, Xu (2020). "Measuring and Relieving the Over-smoothing Problem for Graph Neural Networks from the Topological View". Proceedings of the AAAI Conference on Artificial Intelligence 34 (4): 3438–3445. doi:10.1609/aaai.v34i04.5747. 
  31. ↑ 31.0 31.1 Alon, Uri; Yahav, Eran (2021). "On the Bottleneck of Graph Neural Networks and its Practical Implications". arXiv:2006.05205 [cs.LG].
  32. ↑ Xu, Keyulu; Zhang, Mozhi; Jegelka, Stephanie; Kawaguchi, Kenji (2021). "Optimization of Graph Neural Networks: Implicit Acceleration by Skip Connections and More Depth". arXiv:2105.04550 [cs.LG].
  33. ↑ 33.0 33.1 33.2 Li, Yujia; Tarlow, Daniel; Brockschmidt, Mark; Zemel, Richard (2016). "Gated Graph Sequence Neural Networks". arXiv:1511.05493 [cs.LG].
  34. ↑ 34.0 34.1 Xu, Keyulu; Li, Chengtao; Tian, Yonglong; Sonobe, Tomohiro; Kawarabayashi, Ken-ichi; Jegelka, Stefanie (2018). "Representation Learning on Graphs with Jumping Knowledge Networks". arXiv:1806.03536 [cs.LG].
  35. ↑ Sample, Ian (2 December 2018). "Google's DeepMind predicts 3D shapes of proteins". The Guardian. https://www.theguardian.com/science/2018/dec/02/google-deepminds-ai-program-alphafold-predicts-3d-shapes-of-proteins. 
  36. ↑ "DeepMind's protein-folding AI has solved a 50-year-old grand challenge of biology" (in en). https://www.technologyreview.com/2020/11/30/1012712/deepmind-protein-folding-ai-solved-biology-science-drugs-disease/. 
  37. ↑ Fan, Wenqi; Ma, Yao; Li, Qing; He, Yuan; Zhao, Eric; Tang, Jiliang; Yin, Dawei (2019). Graph Neural Networks for Social Recommendation. pp. 417–426. doi:10.1145/3308558.3313488. ISBN 9781450366748. 
  38. ↑ Cappart, Quentin; Chételat, Didier; Khalil, Elias; Lodi, Andrea; Morris, Christopher; Veličković, Petar (2021). "Combinatorial optimization and reasoning with graph neural networks". arXiv:2102.09544 [cs.LG].
  39. ↑ Mirhoseini, Azalia; Goldie, Anna; Yazgan, Mustafa; Jiang, Joe Wenjie; Songhori, Ebrahim; Wang, Shen; Lee, Young-Joon; Johnson, Eric et al. (2021). "A graph placement methodology for fast chip design". Nature 594 (7862): 207–212. doi:10.1038/s41586-021-03544-w. PMID 34108699. 
  40. ↑ Gasse, Maxime; Chételat, Didier; Ferroni, Nicola; Charlin, Laurent; Lodi, Andrea (2019). "Exact Combinatorial Optimization with Graph Convolutional Neural Networks". arXiv:1906.01629 [cs.LG].
  41. ↑ Wang, Su; Wang, Zhiliang; Zhou, Tao; Sun, Hongbin; Yin, Xia; Han, Dongqi; Zhang, Han; Shi, Xingang et al. (2022). "Threatrace: Detecting and Tracing Host-Based Threats in Node Level Through Provenance Graph Learning". IEEE Transactions on Information Forensics and Security 17: 3972–3987. doi:10.1109/TIFS.2022.3208815. ISSN 1556-6021. https://ieeexplore.ieee.org/document/9899459/;jsessionid=NzAXdLahhjEX-xmrFzOROk4qxoaz40aJFvKcZRgjck8-zCOucJi7!380715771. 
  42. ↑ Wang, Qi; Hassan, Wajih Ul; Li, Ding; Jee, Kangkook; Yu, Xiao (2020). "You Are What You Do: Hunting Stealthy Malware via Data Provenance Analysis.". Network and Distributed Systems Security (NDSS) Symposium. doi:10.14722/ndss.2020.24167. ISBN 978-1-891562-61-7. 
  43. ↑ King, Isaiah J.; Huang, H. Howie (2022). "Euler: Detecting Network Lateral Movement via Scalable Temporal Link Prediction". In Proceedings of the 29th Network and Distributed Systems Security Symposium (NDSS). doi:10.14722/ndss.2022.24107. https://www.ndss-symposium.org/wp-content/uploads/2022-107A-paper.pdf. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Graph_neural_network&oldid=3433325"