Physics:Fermi's interaction
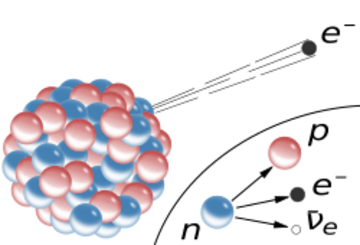
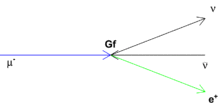
In particle physics, Fermi's interaction (also the Fermi theory of beta decay or the Fermi four-fermion interaction) is an explanation of the beta decay, proposed by Enrico Fermi in 1933.[1] The theory posits four fermions directly interacting with one another (at one vertex of the associated Feynman diagram). This interaction explains beta decay of a neutron by direct coupling of a neutron with an electron, a neutrino (later determined to be an antineutrino) and a proton.[2]
Fermi first introduced this coupling in his description of beta decay in 1933.[3] The Fermi interaction was the precursor to the theory for the weak interaction where the interaction between the proton–neutron and electron–antineutrino is mediated by a virtual W− boson, of which the Fermi theory is the low-energy effective field theory.
History of initial rejection and later publication
Fermi first submitted his "tentative" theory of beta decay to the prestigious science journal Nature, which rejected it "because it contained speculations too remote from reality to be of interest to the reader.[4]" Nature later admitted the rejection to be one of the great editorial blunders in its history.[5] Fermi then submitted revised versions of the paper to Italian and German publications, which accepted and published them in those languages in 1933 and 1934.[6][7][8][9] The paper did not appear at the time in a primary publication in English.[5] An English translation of the seminal paper was published in the American Journal of Physics in 1968.[9]
Fermi found the initial rejection of the paper so troubling that he decided to take some time off from theoretical physics, and do only experimental physics. This would lead shortly to his famous work with activation of nuclei with slow neutrons.
The "tentativo"
Definitions
The theory deals with three types of particles presumed to be in direct interaction: initially a “heavy particle” in the “neutron state” ([math]\displaystyle{ \rho=+1 }[/math]), which then transitions into its “proton state” ([math]\displaystyle{ \rho = -1 }[/math]) with the emission of an electron and a neutrino.
Electron state
- [math]\displaystyle{ \psi = \sum_s \psi_s a_s, }[/math]
where [math]\displaystyle{ \psi }[/math] is the single-electron wavefunction, [math]\displaystyle{ \psi_s }[/math] are its stationary states.
[math]\displaystyle{ a_s }[/math] is the operator which annihilates an electron in state [math]\displaystyle{ s }[/math] which acts on the Fock space as
- [math]\displaystyle{ a_s \Psi(N_1, N_2, \ldots, N_s, \ldots) = (-1)^{N_1 + N_2 + \cdots + N_s - 1} (1 - N_s) \Psi(N_1, N_2, \ldots, 1 - N_s, \ldots). }[/math]
[math]\displaystyle{ a_s^* }[/math] is the creation operator for electron state [math]\displaystyle{ s }[/math]:
- [math]\displaystyle{ a_s^* \Psi(N_1, N_2, \ldots, N_s, \ldots) = (-1)^{N_1 + N_2 + \cdots + N_s - 1} N_s \Psi(N_1, N_2, \ldots, 1 - N_s, \ldots). }[/math]
Neutrino state
Similarly,
- [math]\displaystyle{ \phi = \sum_\sigma \phi_\sigma b_\sigma, }[/math]
where [math]\displaystyle{ \phi }[/math] is the single-neutrino wavefunction, and [math]\displaystyle{ \phi_\sigma }[/math] are its stationary states.
[math]\displaystyle{ b_\sigma }[/math] is the operator which annihilates a neutrino in state [math]\displaystyle{ \sigma }[/math] which acts on the Fock space as
- [math]\displaystyle{ b_\sigma \Phi(M_1, M_2, \ldots, M_\sigma, \ldots) = (-1)^{M_1 + M_2 + \cdots + M_\sigma - 1} (1 - M_\sigma) \Phi(M_1, M_2, \ldots, 1 - M_\sigma, \ldots). }[/math]
[math]\displaystyle{ b_\sigma^* }[/math] is the creation operator for neutrino state [math]\displaystyle{ \sigma }[/math].
Heavy particle state
[math]\displaystyle{ \rho }[/math] is the operator introduced by Heisenberg (later generalized into isospin) that acts on a heavy particle state, which has eigenvalue +1 when the particle is a neutron, and −1 if the particle is a proton. Therefore, heavy particle states will be represented by two-row column vectors, where
- [math]\displaystyle{ \begin{pmatrix}1\\0\end{pmatrix} }[/math]
represents a neutron, and
- [math]\displaystyle{ \begin{pmatrix}0\\1\end{pmatrix} }[/math]
represents a proton (in the representation where [math]\displaystyle{ \rho }[/math] is the usual [math]\displaystyle{ \sigma_z }[/math] spin matrix).
The operators that change a heavy particle from a proton into a neutron and vice versa are respectively represented by
- [math]\displaystyle{ Q = \sigma_x - i \sigma_y = \begin{pmatrix}0 & 1\\ 0 & 0\end{pmatrix} }[/math]
and
- [math]\displaystyle{ Q^* = \sigma_x + i \sigma_y = \begin{pmatrix}0 & 0\\ 1 & 0\end{pmatrix}. }[/math]
[math]\displaystyle{ u_n }[/math] resp. [math]\displaystyle{ v_n }[/math] is an eigenfunction for a neutron resp. proton in the state [math]\displaystyle{ n }[/math].
Hamiltonian
The Hamiltonian is composed of three parts: [math]\displaystyle{ H_\text{h.p.} }[/math], representing the energy of the free heavy particles, [math]\displaystyle{ H_\text{l.p.} }[/math], representing the energy of the free light particles, and a part giving the interaction [math]\displaystyle{ H_\text{int.} }[/math].
- [math]\displaystyle{ H_\text{h.p.} = \frac{1}{2}(1 + \rho)N + \frac{1}{2}(1 - \rho)P, }[/math]
where [math]\displaystyle{ N }[/math] and [math]\displaystyle{ P }[/math] are the energy operators of the neutron and proton respectively, so that if [math]\displaystyle{ \rho = 1 }[/math], [math]\displaystyle{ H_\text{h.p.} = N }[/math], and if [math]\displaystyle{ \rho = -1 }[/math], [math]\displaystyle{ H_\text{h.p.} = P }[/math].
- [math]\displaystyle{ H_\text{l.p.} = \sum_s H_s N_s + \sum_\sigma K_\sigma M_\sigma, }[/math]
where [math]\displaystyle{ H_s }[/math] is the energy of the electron in the [math]\displaystyle{ s^\text{th} }[/math] state in the nucleus's Coulomb field, and [math]\displaystyle{ N_s }[/math] is the number of electrons in that state; [math]\displaystyle{ M_\sigma }[/math] is the number of neutrinos in the [math]\displaystyle{ \sigma^\text{th} }[/math] state, and [math]\displaystyle{ K_\sigma }[/math] energy of each such neutrino (assumed to be in a free, plane wave state).
The interaction part must contain a term representing the transformation of a proton into a neutron along with the emission of an electron and a neutrino (now known to be an antineutrino), as well as a term for the inverse process; the Coulomb force between the electron and proton is ignored as irrelevant to the [math]\displaystyle{ \beta }[/math]-decay process.
Fermi proposes two possible values for [math]\displaystyle{ H_\text{int.} }[/math]: first, a non-relativistic version which ignores spin:
- [math]\displaystyle{ H_\text{int.} = g \left[ Q \psi(x) \phi(x) + Q^* \psi^*(x) \phi^*(x) \right], }[/math]
and subsequently a version assuming that the light particles are four-component Dirac spinors, but that speed of the heavy particles is small relative to [math]\displaystyle{ c }[/math] and that the interaction terms analogous to the electromagnetic vector potential can be ignored:
- [math]\displaystyle{ H_\text{int.} = g \left[ Q \tilde{\psi}^* \delta \psi + Q^* \tilde{\psi} \delta \psi^* \right], }[/math]
where [math]\displaystyle{ \psi }[/math] and [math]\displaystyle{ \phi }[/math] are now four-component Dirac spinors, [math]\displaystyle{ \tilde{\psi} }[/math] represents the Hermitian conjugate of [math]\displaystyle{ \psi }[/math], and [math]\displaystyle{ \delta }[/math] is a matrix
- [math]\displaystyle{ \begin{pmatrix} 0 & -1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 \end{pmatrix}. }[/math]
Matrix elements
The state of the system is taken to be given by the tuple [math]\displaystyle{ \rho, n, N_1, N_2, \ldots, M_1, M_2, \ldots, }[/math] where [math]\displaystyle{ \rho = \pm 1 }[/math] specifies whether the heavy particle is a neutron or proton, [math]\displaystyle{ n }[/math] is the quantum state of the heavy particle, [math]\displaystyle{ N_s }[/math] is the number of electrons in state [math]\displaystyle{ s }[/math] and [math]\displaystyle{ M_\sigma }[/math] is the number of neutrinos in state [math]\displaystyle{ \sigma }[/math].
Using the relativistic version of [math]\displaystyle{ H_\text{int.} }[/math], Fermi gives the matrix element between the state with a neutron in state [math]\displaystyle{ n }[/math] and no electrons resp. neutrinos present in state [math]\displaystyle{ s }[/math] resp. [math]\displaystyle{ \sigma }[/math], and the state with a proton in state [math]\displaystyle{ m }[/math] and an electron and a neutrino present in states [math]\displaystyle{ s }[/math] and [math]\displaystyle{ \sigma }[/math] as
- [math]\displaystyle{ H^{\rho=1, n, N_s=0, M_\sigma=0}_{\rho=-1,m,N_s=1,M_\sigma=1} = \pm g \int v_m^* u_n \tilde{\psi}_s \delta \phi^*_\sigma d\tau, }[/math]
where the integral is taken over the entire configuration space of the heavy particles (except for [math]\displaystyle{ \rho }[/math]). The [math]\displaystyle{ \pm }[/math] is determined by whether the total number of light particles is odd (−) or even (+).
Transition probability
To calculate the lifetime of a neutron in a state [math]\displaystyle{ n }[/math] according to the usual Quantum perturbation theory, the above matrix elements must be summed over all unoccupied electron and neutrino states. This is simplified by assuming that the electron and neutrino eigenfunctions [math]\displaystyle{ \psi_s }[/math] and [math]\displaystyle{ \phi_\sigma }[/math] are constant within the nucleus (i.e., their Compton wavelength is much smaller than the size of the nucleus). This leads to
- [math]\displaystyle{ H^{\rho=1, n, N_s=0, M_\sigma=0}_{\rho=-1,m,N_s=1,M_\sigma=1} = \pm g \tilde{\psi}_s \delta \phi_\sigma^* \int v_m^* u_n d\tau, }[/math]
where [math]\displaystyle{ \psi_s }[/math] and [math]\displaystyle{ \phi_\sigma }[/math] are now evaluated at the position of the nucleus.
According to Fermi's golden rule[further explanation needed], the probability of this transition is
- [math]\displaystyle{ \begin{align} \left|a^{\rho=1, n, N_s=0, M_\sigma=0}_{\rho=-1,m,N_s=1,M_\sigma=1}\right|^2 &= \left|H^{\rho=1, n, N_s=0, M_\sigma=0}_{\rho=-1,m,N_s=1,M_\sigma=1} \times \frac{\exp{\frac{2\pi i}{h} (-W + H_s + K_\sigma) t} - 1}{-W + H_s + K_\sigma}\right|^2 \\ &= 4 \left|H^{\rho=1, n, N_s=0, M_\sigma=0}_{\rho=-1,m,N_s=1,M_\sigma=1}\right|^2 \times \frac{\sin^2\left(\frac{\pi t}{h}(-W + H_s + K_\sigma)\right)}{(-W + H_s + K_\sigma)^2}, \end{align} }[/math]
where [math]\displaystyle{ W }[/math] is the difference in the energy of the proton and neutron states.
Averaging over all positive-energy neutrino spin / momentum directions (where [math]\displaystyle{ \Omega^{-1} }[/math] is the density of neutrino states, eventually taken to infinity), we obtain
- [math]\displaystyle{ \left\langle \left|H^{\rho=1, n, N_s=0, M_\sigma=0}_{\rho=-1,m,N_s=1,M_\sigma=1}\right|^2 \right \rangle_\text{avg} = \frac{g^2}{4\Omega} \left|\int v_m^* u_n d\tau\right|^2 \left( \tilde{\psi}_s \psi_s - \frac{\mu c^2}{K_\sigma} \tilde{\psi}_s \beta \psi_s\right), }[/math]
where [math]\displaystyle{ \mu }[/math] is the rest mass of the neutrino and [math]\displaystyle{ \beta }[/math] is the Dirac matrix.
Noting that the transition probability has a sharp maximum for values of [math]\displaystyle{ p_\sigma }[/math] for which [math]\displaystyle{ -W + H_s + K_\sigma = 0 }[/math], this simplifies to [further explanation needed]
- [math]\displaystyle{ t\frac{8\pi^3 g^2}{h^4} \times \left| \int v_m^* u_n d\tau \right|^2 \frac{p_\sigma^2}{v_\sigma}\left(\tilde{\psi}_s \psi_s - \frac{\mu c^2}{K_\sigma} \tilde{\psi}_s \beta \psi_s\right), }[/math]
where [math]\displaystyle{ p_\sigma }[/math] and [math]\displaystyle{ K_\sigma }[/math] is the values for which [math]\displaystyle{ -W + H_s + K_\sigma = 0 }[/math].
Fermi makes three remarks about this function:
- Since the neutrino states are considered to be free, [math]\displaystyle{ K_\sigma \gt \mu c^2 }[/math] and thus the upper limit on the continuous [math]\displaystyle{ \beta }[/math]-spectrum is [math]\displaystyle{ H_s \leq W - \mu c^2 }[/math].
- Since for the electrons [math]\displaystyle{ H_s \gt mc^2 }[/math], in order for [math]\displaystyle{ \beta }[/math]-decay to occur, the proton–neutron energy difference must be [math]\displaystyle{ W \geq (m + \mu)c^2 }[/math]
- The factor
- [math]\displaystyle{ Q_{mn}^* = \int v_m^* u_n d\tau }[/math]
- in the transition probability is normally of magnitude 1, but in special circumstances it vanishes; this leads to (approximate) selection rules for [math]\displaystyle{ \beta }[/math]-decay.
Forbidden transitions
As noted above, when the inner product [math]\displaystyle{ Q_{mn}^* }[/math] between the heavy particle states [math]\displaystyle{ u_n }[/math] and [math]\displaystyle{ v_m }[/math] vanishes, the associated transition is "forbidden" (or, rather, much less likely than in cases where it is closer to 1).
If the description of the nucleus in terms of the individual quantum states of the protons and neutrons is good, [math]\displaystyle{ Q_{mn}^* }[/math] vanishes unless the neutron state [math]\displaystyle{ u_n }[/math] and the proton state [math]\displaystyle{ v_m }[/math] have the same angular momentum; otherwise, the angular momentum of the whole nucleus before and after the decay must be used.
Influence
Shortly after Fermi's paper appeared, Werner Heisenberg noted in a letter to Wolfgang Pauli[10] that the emission and absorption of neutrinos and electrons in the nucleus should, at the second order of perturbation theory, lead to an attraction between protons and neutrons, analogously to how the emission and absorption of photons leads to the electromagnetic force. He found that the force would be of the form [math]\displaystyle{ \frac{\text{Const.}}{r^5} }[/math], but that contemporary experimental data led to a value that was too small by a factor of a million.[11]
The following year, Hideki Yukawa picked up on this idea,[12] but in his theory the neutrinos and electrons were replaced by a new hypothetical particle with a rest mass approximately 200 times heavier than the electron.[13]
Later developments
Fermi's four-fermion theory describes the weak interaction remarkably well. Unfortunately, the calculated cross-section, or probability of interaction, grows as the square of the energy [math]\displaystyle{ \sigma \approx G_{\rm F}^2 E^2 }[/math]. Since this cross section grows without bound, the theory is not valid at energies much higher than about 100 GeV. Here GF is the Fermi constant, which denotes the strength of the interaction. This eventually led to the replacement of the four-fermion contact interaction by a more complete theory (UV completion)—an exchange of a W or Z boson as explained in the electroweak theory.
The interaction could also explain muon decay via a coupling of a muon, electron-antineutrino, muon-neutrino and electron, with the same fundamental strength of the interaction. This hypothesis was put forward by Gershtein and Zeldovich and is known as the Vector Current Conservation hypothesis.[14]
In the original theory, Fermi assumed that the form of interaction is a contact coupling of two vector currents. Subsequently, it was pointed out by Lee and Yang that nothing prevented the appearance of an axial, parity violating current, and this was confirmed by experiments carried out by Chien-Shiung Wu.[15][16]
The inclusion of parity violation in Fermi's interaction was done by George Gamow and Edward Teller in the so-called Gamow–Teller transitions which described Fermi's interaction in terms of parity-violating "allowed" decays and parity-conserving "superallowed" decays in terms of anti-parallel and parallel electron and neutrino spin states respectively. Before the advent of the electroweak theory and the Standard Model, George Sudarshan and Robert Marshak, and also independently Richard Feynman and Murray Gell-Mann, were able to determine the correct tensor structure (vector minus axial vector, V − A) of the four-fermion interaction.[17][18]
Fermi constant
The most precise experimental determination of the Fermi constant comes from measurements of the muon lifetime, which is inversely proportional to the square of GF (when neglecting the muon mass against the mass of the W boson).[19] In modern terms, the "reduced Fermi constant", that is, the constant in natural units is[3][20]
- [math]\displaystyle{ G_{\rm F}^0=\frac{G_{\rm F}}{(\hbar c)^3}=\frac{\sqrt{2}}{8}\frac{g^{2}}{M_{\rm W}^{2} c^4}=1.1663787(6)\times10^{-5} \; \textrm{GeV}^{-2} \approx 4.5437957\times10^{14} \; \textrm{J}^{-2}\ . }[/math]
Here, g is the coupling constant of the weak interaction, and MW is the mass of the W boson, which mediates the decay in question.
In the Standard Model, the Fermi constant is related to the Higgs vacuum expectation value
- [math]\displaystyle{ v = \left(\sqrt{2} \, G_{\rm F}^0\right)^{-1/2} \simeq 246.22 \; \textrm{GeV} }[/math].[21]
More directly, approximately (tree level for the standard model),
- [math]\displaystyle{ G_{\rm F}^0\simeq \frac {\pi \alpha}{\sqrt{2}~ M_{\rm W}^2 (1- M^2_{\rm W}/M^2_{\rm Z} )}. }[/math]
This can be further simplified in terms of the Weinberg angle using the relation between the W and Z bosons with [math]\displaystyle{ M_\text{Z}=\frac{M_\text{W}}{\cos\theta_\text{W}} }[/math], so that
- [math]\displaystyle{ G_{\rm F}^0\simeq \frac {\pi \alpha}{\sqrt{2}~ M_{\rm Z}^{2}\cos^{2}\theta_{\rm W}\sin^{2}\theta_{\rm W}}. }[/math]
References
- ↑ Yang, C. N. (2012). "Fermi's β-decay Theory". Asia Pacific Physics Newsletter 1 (1): 27–30. doi:10.1142/s2251158x12000045.
- ↑ Feynman, R.P. (1962). Theory of Fundamental Processes. W. A. Benjamin. Chapters 6 & 7.
- ↑ 3.0 3.1 Griffiths, D. (2009). Introduction to Elementary Particles (2nd ed.). pp. 314–315. ISBN 978-3-527-40601-2.
- ↑ Pais, Abraham (1986). Inward Bound. Oxford: Oxford University Press. p. 418. ISBN 0-19-851997-4. https://archive.org/details/inwardboundofmat00pais_0.
- ↑ 5.0 5.1 Close, Frank (2012-02-23). Neutrino. Oxford University Press. https://books.google.com/books?id=A-MVDAAAQBA. Retrieved 2017-05-05.
- ↑ Fermi, E. (1933). "Tentativo di una teoria dei raggi β" (in it). La Ricerca Scientifica 2 (12).
- ↑ Fermi, E. (1934). "Tentativo di una teoria dei raggi β" (in it). Il Nuovo Cimento 11 (1): 1–19. doi:10.1007/BF02959820. Bibcode: 1934NCim...11....1F.
- ↑ Fermi, E. (1934). "Versuch einer Theorie der beta-Strahlen. I" (in de). Zeitschrift für Physik 88: 161. doi:10.1007/BF01351864. Bibcode: 1934ZPhy...88..161F.
- ↑ 9.0 9.1 Wilson, F. L. (1968). "Fermi's Theory of Beta Decay". American Journal of Physics 36 (12): 1150–1160. doi:10.1119/1.1974382. Bibcode: 1968AmJPh..36.1150W. http://microboone-docdb.fnal.gov/cgi-bin/RetrieveFile?docid=953;filename=FermiBetaDecay1934.pdf;version=1. Includes complete English translation of Fermi's 1934 paper in German
- ↑ Pauli, Wolfgang (1985). Scientific Correspondence with Bohr, Einstein, Heisenberg a.o. Volume II:1930–1939. Springer-Verlag Berlin Heidelberg GmbH. p. 250, letter #341, Heisenberg to Pauli, January 18th 1934.
- ↑ Brown, Laurie M (1996). The Origin of the Concept of Nuclear Forces. Institute of Physics Publishing. Section 3.3. https://archive.org/details/originofconcepto0000brow.
- ↑ Yukawa, H. (1935). "On the interaction of elementary particles. I." (in en). Proceedings of the Physico-Mathematical Society of Japan 17: 1.
- ↑ Mehra, Jagdish (2001). The Historical Development of Quantum Theory, Volume 6 Part 2 (1932–1941). Springer. p. 832.
- ↑ Gerstein, S. S.; Zeldovich, Ya. B. (1955). "Meson corrections in the theory of beta decay". Zh. Eksp. Teor. Fiz.: 698–699.
- ↑ Lee, T. D.; Yang, C. N. (1956). "Question of Parity Conservation in Weak Interactions". Physical Review 104 (1): 254–258. doi:10.1103/PhysRev.104.254. Bibcode: 1956PhRv..104..254L.
- ↑ Wu, C. S.; Ambler, E; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P. (1957). "Experimental Test of Parity Conservation in Beta Decay". Physical Review 105 (4): 1413–1415. doi:10.1103/PhysRev.105.1413. Bibcode: 1957PhRv..105.1413W.
- ↑ Feynman, R. P.; Gell-Mann, M. (1958). "Theory of the Fermi interaction". Physical Review 109 (1): 193. doi:10.1103/physrev.109.193. Bibcode: 1958PhRv..109..193F. http://authors.library.caltech.edu/3514/1/FEYpr58.pdf.
- ↑ Sudarshan, E. C.; Marshak, R. E. (1958). "Chirality invariance and the universal Fermi interaction". Physical Review 109 (5): 1860. doi:10.1103/physrev.109.1860.2. Bibcode: 1958PhRv..109.1860S.
- ↑ Chitwood, D. B. et al. (2007). "Improved Measurement of the Positive-Muon Lifetime and Determination of the Fermi Constant". Physical Review Letters 99 (3): 032001. doi:10.1103/PhysRevLett.99.032001. PMID 17678280. Bibcode: 2007PhRvL..99c2001C.
- ↑ "CODATA Value: Fermi coupling constant". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2015. http://physics.nist.gov/cgi-bin/cuu/Value?gf.
- ↑ Plehn, T.; Rauch, M. (2005). "Quartic Higgs coupling at hadron colliders". Physical Review D 72 (5): 053008. doi:10.1103/PhysRevD.72.053008. Bibcode: 2005PhRvD..72e3008P.