Physics:Wilson loop
In quantum field theory, Wilson loops are gauge invariant operators arising from the parallel transport of gauge variables around closed loops. They encode all gauge information of the theory, allowing for the construction of loop representations which fully describe gauge theories in terms of these loops. In pure gauge theory they play the role of order operators for confinement, where they satisfy what is known as the area law. Originally formulated by Kenneth G. Wilson in 1974, they were used to construct links and plaquettes which are the fundamental parameters in lattice gauge theory.[1] Wilson loops fall into the broader class of loop operators, with some other notable examples being 't Hooft loops, which are magnetic duals to Wilson loops, and Polyakov loops, which are the thermal version of Wilson loops.
Definition
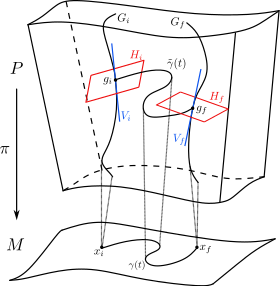
To properly define Wilson loops in gauge theory requires considering the fiber bundle formulation of gauge theories.[2] Here for each point in the [math]\displaystyle{ d }[/math]-dimensional spacetime [math]\displaystyle{ M }[/math] there is a copy of the gauge group [math]\displaystyle{ G }[/math] forming what's known as a fiber of the fibre bundle. These fiber bundles are called principal bundles. Locally the resulting space looks like [math]\displaystyle{ \mathbb R^d \times G }[/math] although globally it can have some twisted structure depending on how different fibers are glued together.
The issue that Wilson lines resolve is how to compare points on fibers at two different spacetime points. This is analogous to parallel transport in general relativity which compares tangent vectors that live in the tangent spaces at different points. For principal bundles there is a natural way to compare different fiber points through the introduction of a connection, which is equivalent to introducing a gauge field. This is because a connection is a way to separate out the tangent space of the principal bundle into two subspaces known as the vertical and horizontal subspaces.[3] The former consists of all vectors pointing along the fiber [math]\displaystyle{ G }[/math] while the latter consists of vectors that are perpendicular to the fiber. This allows for the comparison of fiber values at different spacetime points by connecting them with curves in the principal bundle whose tangent vectors always live in the horizontal subspace, so the curve is always perpendicular to any given fiber.
If the starting fiber is at coordinate [math]\displaystyle{ x_i }[/math] with a starting point of the identity [math]\displaystyle{ g_i=e }[/math], then to see how this changes when moving to another spacetime coordinate [math]\displaystyle{ x_f }[/math], one needs to consider some spacetime curve [math]\displaystyle{ \gamma:[0,1]\rightarrow M }[/math] between [math]\displaystyle{ x_i }[/math] and [math]\displaystyle{ x_f }[/math]. The corresponding curve in the principal bundle, known as the horizontal lift of [math]\displaystyle{ \gamma(t) }[/math], is the curve [math]\displaystyle{ \tilde \gamma(t) }[/math] such that [math]\displaystyle{ \tilde \gamma(0) = g_i }[/math] and that its tangent vectors always lie in the horizontal subspace. The fiber bundle formulation of gauge theory reveals that the Lie-algebra valued gauge field [math]\displaystyle{ A_\mu(x) = A^a_\mu(x)T^a }[/math] is equivalent to the connection that defines the horizontal subspace, so this leads to a differential equation for the horizontal lift
- [math]\displaystyle{ i\frac{dg(t)}{dt} = A_\mu(x)\frac{dx^\mu}{dt} g(t). }[/math]
This has a unique formal solution called the Wilson line between the two points
- [math]\displaystyle{ g_f(t_f) = W[x_i, x_f] = \mathcal P\exp\bigg( i \int_{x_i}^{x_f}A_\mu dx^\mu \bigg), }[/math]
where [math]\displaystyle{ \mathcal P }[/math] is the path-ordering operator, which is unnecessary for abelian theories. The horizontal lift starting at some initial fiber point other than the identity merely requires multiplication by the initial element of the original horizontal lift. More generally, it holds that if [math]\displaystyle{ \tilde \gamma'(0) = \tilde \gamma(0)g }[/math] then [math]\displaystyle{ \tilde \gamma'(t) = \tilde \gamma(t)g }[/math] for all [math]\displaystyle{ t\geq0 }[/math].
Under a local gauge transformation [math]\displaystyle{ g(x) }[/math] the Wilson line transforms as
- [math]\displaystyle{ W[x_i, x_f] \rightarrow g(x_f) W[x_i, x_f] g^{-1}(x_i). }[/math]
This gauge transformation property is often used to directly introduce the Wilson line in the presence of matter fields [math]\displaystyle{ \phi(x) }[/math] transforming in the fundamental representation of the gauge group, where the Wilson line is an operator that makes the combination [math]\displaystyle{ \phi(x_i)^\dagger W[x_i,x_f]\phi(x_f) }[/math] gauge invariant.[4] It allows for the comparison of the matter field at different points in a gauge invariant way. Alternatively, the Wilson lines can also be introduced by adding an infinitely heavy test particle charged under the gauge group. Its charge forms a quantized internal Hilbert space, which can be integrated out, yielding the Wilson line as the world-line of the test particle.[5] In quantum field theory this works whether or not there actually is any matter content in the theory. However, the swampland conjecture known as the completeness conjecture claims that in a consistent theory of quantum gravity, every Wilson line and 't Hooft line of a particular charge consistent with the Dirac quantization condition must have a corresponding particle of that charge be present in the theory.[6] Decoupling these particles by taking the infinite mass limit no longer works since this would form black holes.
The trace of closed Wilson lines is a gauge invariant quantity known as the Wilson loop
[math]\displaystyle{ W[\gamma] = \text{tr}\bigg[\mathcal P \exp\bigg( i \oint_\gamma A_\mu dx^\mu\bigg)\bigg]. }[/math]
Mathematically the term within the trace is known as the holonomy, which describes a mapping of the fiber into itself upon horizontal lift along a closed loop. The set of all holonomies itself forms a group, which for principal bundles must be a subgroup of the gauge group. Wilson loops satisfy the reconstruction property where knowing the set of Wilson loops for all possible loops allows for the reconstruction of all gauge invariant information about the gauge connection.[7] Formally the set of all Wilson loops forms an overcomplete basis of solutions to the Gauss' law constraint.
The set of all Wilson lines is in one-to-one correspondence with the representations of the gauge group. This can be reformulated in terms of Lie algebra language using the weight lattice of the gauge group [math]\displaystyle{ \Lambda_w }[/math]. In this case the types of Wilson loops are in one-to-one correspondence with [math]\displaystyle{ \Lambda_w/W }[/math] where [math]\displaystyle{ W }[/math] is the Weyl group.[8]
Hilbert space operators
An alternative view of Wilson loops is to consider them as operators acting on the Hilbert space of states in Minkowski signature.[5] Since the Hilbert space lives on a single time slice, the only Wilson loops that can act as operators on this space are ones formed using spacelike loops. Such operators [math]\displaystyle{ W[\gamma] }[/math] create a closed loop of electric flux, which can be seen by noting that the electric field operator [math]\displaystyle{ E^i }[/math] is nonzero on the loop [math]\displaystyle{ E^iW[\gamma]|0\rangle \neq 0 }[/math] but it vanishes everywhere else. Using Stokes theorem it follows that the spatial loop measures the magnetic flux through the loop.[9]
Order operator
Since temporal Wilson lines correspond to the configuration created by infinitely heavy stationary quarks, Wilson loop associated with a rectangular loop [math]\displaystyle{ \gamma }[/math] with two temporal components of length [math]\displaystyle{ T }[/math] and two spatial components of length [math]\displaystyle{ r }[/math], can be interpreted as a quark-antiquark pair at fixed separation. Over large times the vacuum expectation value of the Wilson loop projects out the state with the minimum energy, which is the potential [math]\displaystyle{ V(r) }[/math] between the quarks.[10] The excited states with energy [math]\displaystyle{ V(r)+\Delta E }[/math] are exponentially suppressed with time and so the expectation value goes as
- [math]\displaystyle{ \langle W[\gamma]\rangle \sim e^{-TV(r)}(1+\mathcal O(e^{-T\Delta E})), }[/math]
making the Wilson loop useful for calculating the potential between quark pairs. This potential must necessarily be a monotonically increasing and concave function of the quark separation.[11][12] Since spacelike Wilson loops are not fundamentally different from the temporal ones, the quark potential is really directly related to the pure Yang–Mills theory structure and is a phenomenon independent of the matter content.[13]
Elitzur's theorem ensures that local non-gauge invariant operators cannot have a non-zero expectation values. Instead one must use non-local gauge invariant operators as order parameters for confinement. The Wilson loop is exactly such an order parameter in pure Yang–Mills theory, where in the confining phase its expectation value follows the area law[14]
- [math]\displaystyle{ \langle W[\gamma]\rangle \sim e^{-aA[\gamma]} }[/math]
for a loop that encloses an area [math]\displaystyle{ A[\gamma] }[/math]. This is motivated from the potential between infinitely heavy test quarks which in the confinement phase is expected to grow linearly [math]\displaystyle{ V(r) \sim \sigma r }[/math] where [math]\displaystyle{ \sigma }[/math] is known as the string tension. Meanwhile, in the Higgs phase the expectation value follows the perimeter law
- [math]\displaystyle{ \langle W[\gamma]\rangle \sim e^{-bL[\gamma]}, }[/math]
where [math]\displaystyle{ L[\gamma] }[/math] is the perimeter length of the loop and [math]\displaystyle{ b }[/math] is some constant. The area law of Wilson loops can be used to demonstrate confinement in certain low dimensional theories directly, such as for the Schwinger model whose confinement is driven by instantons.[15]
Lattice formulation
In lattice field theory, Wilson lines and loops play a fundamental role in formulating gauge fields on the lattice. The smallest Wilson lines on the lattice, those between two adjacent lattice points, are known as links, with a single link starting from a lattice point [math]\displaystyle{ n }[/math] going in the [math]\displaystyle{ \mu }[/math] direction denoted by [math]\displaystyle{ U_\mu(n) }[/math]. Four links around a single square are known as a plaquette, with their trace forming the smallest Wilson loop.[16] It is these plaquettes that are used to construct the lattice gauge action known as the Wilson action. Larger Wilson loops are expressed as products of link variables along some loop [math]\displaystyle{ \gamma }[/math], denoted by[17]
- [math]\displaystyle{ L[U] = \text{tr} \bigg[\prod_{n \in \gamma} U_\mu(n)\bigg]. }[/math]
These Wilson loops are used to study confinement and quark potentials numerically. Linear combinations of Wilson loops are also used as interpolating operators that give rise to glueball states.[18] The glueball masses can then be extracted from the correlation function between these interpolators.[19]
The lattice formulation of the Wilson loops also allows for an analytic demonstration of confinement in the strongly coupled phase, assuming the quenched approximation where quark loops are neglected.[20] This is done by expanding out the Wilson action as a power series of traces of plaquettes, where the first non-vanishing term in the expectation value of the Wilson loop in an [math]\displaystyle{ \text{SU}(3) }[/math] gauge theory gives rise to an area law with a string tension of the form[21][22]
- [math]\displaystyle{ \sigma = - \frac{1}{a^2}\ln \bigg(\frac{\beta}{18}\bigg)(1+\mathcal O(\beta)), }[/math]
where [math]\displaystyle{ \beta =6/g^2 }[/math] is the inverse coupling constant and [math]\displaystyle{ a }[/math] is the lattice spacing. While this argument holds for both the abelian and non-abelian case, compact electrodynamics only exhibits confinement at strong coupling, with there being a phase transition to the Coulomb phase at [math]\displaystyle{ \beta \sim 1.01 }[/math], leaving the theory deconfined at weak coupling.[23][24] Such a phase transition is not believed to exist for [math]\displaystyle{ \text{SU}(N) }[/math] gauge theories at zero temperature, instead they exhibit confinement at all values of the coupling constant.
Properties
Makeenko–Migdal loop equation
Similarly to the functional derivative which acts on functions of functions, functions of loops admit two types of derivatives called the area derivative and the perimeter derivative. To define the former, consider a contour [math]\displaystyle{ \gamma }[/math] and another contour [math]\displaystyle{ \gamma_{\delta \sigma_{\mu\nu}} }[/math] which is the same contour but with an extra small loop at [math]\displaystyle{ x }[/math] in the [math]\displaystyle{ \mu }[/math]-[math]\displaystyle{ \nu }[/math] plane with area [math]\displaystyle{ \delta \sigma_{\mu\nu}=dx_\mu \wedge dx_\nu }[/math]. Then the area derivative of the loop functional [math]\displaystyle{ F[\gamma] }[/math] is defined through the same idea as the usual derivative, as the normalized difference between the functional of the two loops[25]
- [math]\displaystyle{ \frac{\delta F[\gamma]}{\delta \sigma_{\mu\nu}(x)} = \frac{1}{\delta \sigma_{\mu\nu}(x)}[F[\gamma_{\delta \sigma_{\mu\nu}}]-F[\gamma]]. }[/math]
The perimeter derivative is similarly defined whereby now [math]\displaystyle{ \gamma_{\delta x_\mu} }[/math] is a slight deformation of the contour [math]\displaystyle{ \gamma }[/math] which at position [math]\displaystyle{ x }[/math] has a small extruding loop of length [math]\displaystyle{ \delta x_\mu }[/math] in the [math]\displaystyle{ \mu }[/math] direction and of zero area. The perimeter derivative [math]\displaystyle{ \partial_\mu^x }[/math] of the loop functional is then defined as
- [math]\displaystyle{ \partial_\mu^x F[\gamma] = \frac{1}{\delta x_\mu}[F[\gamma_{\delta x_\mu}]-F[\gamma]]. }[/math]
In the large N-limit, the Wilson loop vacuum expectation value satisfies a closed functional form equation called the Makeenko–Migdal equation[26]
- [math]\displaystyle{ \partial^x_\mu \frac{\delta}{\delta \sigma_{\mu\nu}(x)}\langle W[\gamma]\rangle = g^2 N \oint_\gamma dy_\nu \delta^{(D)}(x-y) \langle W[\gamma_{yx}]\rangle \langle W[\gamma_{xy}]\rangle. }[/math]
Here [math]\displaystyle{ \gamma = \gamma_{xy}\cup \gamma_{yx} }[/math] with [math]\displaystyle{ \gamma_{xy} }[/math] being a line that does not close from [math]\displaystyle{ x }[/math] to [math]\displaystyle{ y }[/math], with the two points however close to each other. The equation can also be written for finite [math]\displaystyle{ N }[/math], but in this case it does not factorize and instead leads to expectation values of products of Wilson loops, rather than the product of their expectation values.[27] This gives rise to an infinite chain of coupled equations for different Wilson loop expectation values, analogous to the Schwinger–Dyson equations. The Makeenko–Migdal equation has been solved exactly in two dimensional [math]\displaystyle{ \text{U}(\infty) }[/math] theory.[28]
Mandelstam identities
Gauge groups that admit fundamental representations in terms of [math]\displaystyle{ N\times N }[/math] matrices have Wilson loops that satisfy a set of identities called the Mandelstam identities, with these identities reflecting the particular properties of the underlying gauge group.[29] The identities apply to loops formed from two or more subloops, with [math]\displaystyle{ \gamma = \gamma_2 \circ \gamma_1 }[/math] being a loop formed by first going around [math]\displaystyle{ \gamma_1 }[/math] and then going around [math]\displaystyle{ \gamma_2 }[/math].
The Mandelstam identity of the first kind states that [math]\displaystyle{ W[\gamma_1\circ \gamma_2] = W[\gamma_2 \circ \gamma_1] }[/math], with this holding for any gauge group in any dimension. Mandelstam identities of the second kind are acquired by noting that in [math]\displaystyle{ N }[/math] dimensions, any object with [math]\displaystyle{ N+1 }[/math] totally antisymmetric indices vanishes, meaning that [math]\displaystyle{ \delta^{a_1}_{[b_1}\delta^{a_2}_{b_2}\cdots \delta^{a_{N+1}}_{b_{N+1}]} = 0 }[/math]. In the fundamental representation, the holonomies used to form the Wilson loops are [math]\displaystyle{ N\times N }[/math] matrix representations of the gauge groups. Contracting [math]\displaystyle{ N+1 }[/math] holonomies with the delta functions yields a set of identities between Wilson loops. These can be written in terms the objects [math]\displaystyle{ M_K }[/math] defined iteratively so that [math]\displaystyle{ M_1[\gamma] = W[\gamma] }[/math] and
- [math]\displaystyle{ (K+1)M_{K+1}[\gamma_1, \dots, \gamma_{K+1}] = W[\gamma_{K+1}]M_K[\gamma_1,\dots, \gamma_K] - M_K[\gamma_1 \circ \gamma_{K+1},\gamma_2, \dots, \gamma_K] -\cdots - M_K[\gamma_1, \gamma_2, \dots, \gamma_K\circ \gamma_{K+1}]. }[/math]
In this notation the Mandelstam identities of the second kind are[30]
- [math]\displaystyle{ M_{N+1}[\gamma_1, \dots, \gamma_{N+1}] = 0. }[/math]
For example, for a [math]\displaystyle{ \text{U}(1) }[/math] gauge group this gives [math]\displaystyle{ W[\gamma_1]W[\gamma_2] = W[\gamma_1\circ \gamma_2] }[/math].
If the fundamental representation are matrices of unit determinant, then it also holds that [math]\displaystyle{ M_N(\gamma, \dots, \gamma)=1 }[/math]. For example, applying this identity to [math]\displaystyle{ \text{SU}(2) }[/math] gives
- [math]\displaystyle{ W[\gamma_1]W[\gamma_2] = W[\gamma_1\circ \gamma_2^{-1}]+W[\gamma_1\circ \gamma_2]. }[/math]
Fundamental representations consisting of unitary matrices satisfy [math]\displaystyle{ W[\gamma] = W^*[\gamma^{-1}] }[/math]. Furthermore, while the equality [math]\displaystyle{ W[I] = N }[/math] holds for all gauge groups in the fundamental representations, for unitary groups it moreover holds that [math]\displaystyle{ |W[\gamma]|\leq N }[/math].
Renormalization
Since Wilson loops are operators of the gauge fields, the regularization and renormalization of the underlying Yang–Mills theory fields and couplings does not prevent the Wilson loops from requiring additional renormalization corrections. In a renormalized Yang–Mills theory, the particular way that the Wilson loops get renormalized depends on the geometry of the loop under consideration. The main features are[31][32][33][34]
- Smooth non-intersecting curve: This can only have linear divergences proportional to the contour which can be removed through multiplicative renormalization.
- Non-intersecting curve with cusps: Each cusp results in an additional local multiplicative renormalization factor [math]\displaystyle{ Z[\phi] }[/math] that depends on the cusp angle [math]\displaystyle{ \phi }[/math].
- Self-intersections: This leads to operator mixing between the Wilson loops associated with the full loop and the subloops.
- Lightlike segments: These give rise to additional logarithmic divergences.
Additional applications
Scattering amplitudes
Wilson loops play a role in the theory of scattering amplitudes where a set of dualities between them and special types of scattering amplitudes has been found.[35] These have first been suggested at strong coupling using the AdS/CFT correspondence.[36] For example, in [math]\displaystyle{ \mathcal N=4 }[/math] supersymmetric Yang–Mills theory maximally helicity violating amplitudes factorize into a tree-level component and a loop level correction.[37] This loop level correction does not depend on the helicities of the particles, but it was found to be dual to certain polygonal Wilson loops in the large [math]\displaystyle{ N }[/math] limit, up to finite terms. While this duality was initially only suggested in the maximum helicity violating case, there are arguments that it can be extended to all helicity configurations by defining appropriate supersymmetric generalizations of the Wilson loop.[38]
String theory compactifications
In compactified theories, zero mode gauge field states that are locally pure gauge configurations but are globally inequivalent to the vacuum are parameterized by closed Wilson lines in the compact direction. The presence of these on a compactified open string theory is equivalent under T-duality to a theory with non-coincident D-branes, whose separations are determined by the Wilson lines.[39] Wilson lines also play a role in orbifold compactifications where their presence leads to greater control of gauge symmetry breaking, giving a better handle on the final unbroken gauge group and also providing a mechanism for controlling the number of matter multiplets left after compactification.[40] These properties make Wilson lines important in compactifications of superstring theories.[41][42]
Topological field theory
In a topological field theory, the expectation value of Wilson loops does not change under smooth deformations of the loop since the field theory does not depend on the metric.[43] For this reason, Wilson loops are key observables on in these theories and are used to calculate global properties of the manifold. In [math]\displaystyle{ 2+1 }[/math] dimensions they are closely related to knot theory with the expectation value of a product of loops depending only on the manifold structure and on how the loops are tied together. This led to the famous connection made by Edward Witten where he used Wilson loops in Chern–Simons theory to relate their partition function to Jones polynomials of knot theory.[44]
See also
References
- ↑ Wilson, K.G. (1974). "Confinement of quarks". Phys. Rev. D 10 (8): 2445–2459. doi:10.1103/PhysRevD.10.2445. Bibcode: 1974PhRvD..10.2445W. https://link.aps.org/doi/10.1103/PhysRevD.10.2445.
- ↑ Nakahara, M. (2003). "10". Geometry, Topology and Physics (2 ed.). CRC Press. pp. 374–418. ISBN 978-0750306065.
- ↑ Eschrig, H. (2011). "7". Topology and Geometry for Physics. Lecture Notes in Physics. Springer. pp. 220–222. ISBN 978-3-642-14699-2.
- ↑ Schwartz, M. D. (2014). "25". Quantum Field Theory and the Standard Model. Cambridge University Press. pp. 488–493. ISBN 9781107034730.
- ↑ 5.0 5.1 Tong, D. (2018), "2", Lecture Notes on Gauge Theory, https://www.damtp.cam.ac.uk/user/tong/gaugetheory.html
- ↑ Banks, T.; Seiberg, N. (2011). "Symmetries and Strings in Field Theory and Gravity". Phys. Rev. D 83: 084019. doi:10.1103/PhysRevD.83.084019.
- ↑ Giles, R. (1981). "Reconstruction of gauge potentials from Wilson loops". Phys. Rev. D 24 (8): 2160–2168. doi:10.1103/PhysRevD.24.2160. Bibcode: 1981PhRvD..24.2160G. https://link.aps.org/doi/10.1103/PhysRevD.24.2160.
- ↑ Ofer, A.; Seiberg, N.; Tachikawa, Yuji (2013). "Reading between the lines of four-dimensional gauge theories". JHEP 2013 (8): 115. doi:10.1007/JHEP08(2013)115. Bibcode: 2013JHEP...08..115A.
- ↑ Peskin, Michael E.; Schroeder, Daniel V. (1995). "15". An Introduction to Quantum Field Theory. Westview Press. p. 492. ISBN 9780201503975.
- ↑ Rothe, H.J. (2005). "7". Lattice Gauge Theories: An Introduction. World Scientific Lecture Notes in Physics: Volume 43. 82. World Scientific Publishing. pp. 95–108. doi:10.1142/8229. ISBN 978-9814365857. https://library.oapen.org/handle/20.500.12657/50492.
- ↑ Seiler, E. (1978). "Upper bound on the color-confining potential". Phys. Rev. D 18 (2): 482–483. doi:10.1103/PhysRevD.18.482. Bibcode: 1978PhRvD..18..482S. https://link.aps.org/doi/10.1103/PhysRevD.18.482.
- ↑ Bachas, C. (1986). "Concavity of the quarkonium potential". Phys. Rev. D 33 (9): 2723–2725. doi:10.1103/PhysRevD.33.2723. PMID 9956963. Bibcode: 1986PhRvD..33.2723B. https://link.aps.org/doi/10.1103/PhysRevD.33.2723.
- ↑ Greensite, J. (2020). "4". An Introduction to the Confinement Problem (2 ed.). Springer. pp. 37–40. ISBN 978-3030515621.
- ↑ Makeenko, Y. (2002). "6". Methods of Contemporary Gauge Theory. Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press. pp. 117–118. doi:10.1017/CBO9780511535147. ISBN 978-0521809115.
- ↑ Paranjape, M. (2017). "9". The Theory and Applications of Instanton Calculations. Cambridge University Press. p. 168. ISBN 978-1107155473.
- ↑ Baulieu, L.; Iliopoulos, J.; Sénéor, R. (2017). "25". From Classical to Quantum Fields. Oxford University Press. p. 720. ISBN 978-0198788409.
- ↑ Montvay, I.; Munster, G. (1994). "43". Quantum Fields on a Lattice. Cambridge Monographs on Mathematical Physics. Cambridge: Cambridge University Press. p. 105. doi:10.1017/CBO9780511470783. ISBN 9780511470783.
- ↑ DeGrand, T.; DeTar, C. (2006). "11". Lattice Methods for Quantum Chromodynamics. World Scientific Publishing. pp. 232–233. doi:10.1142/6065. ISBN 978-9812567277. Bibcode: 2006lmqc.book.....D.
- ↑ Chen, Y. (2006). "Glueball spectrum and matrix elements on anisotropic lattices". Phys. Rev. D 73 (1): 014516. doi:10.1103/PhysRevD.73.014516. Bibcode: 2006PhRvD..73a4516C.
- ↑ Yndurain, F.J. (2006). "9". The Theory of Quark and Gluon Interactions (4 ed.). Springer. p. 383. ISBN 978-3540332091.
- ↑ Gattringer, C.; Lang, C.B. (2009). "3". Quantum Chromodynamics on the Lattice: An Introductory Presentation. Lecture Notes in Physics 788. Springer. pp. 58–62. doi:10.1007/978-3-642-01850-3. ISBN 978-3642018497.
- ↑ Drouffe, J.M.; Zuber, J.B. (1983). "Strong coupling and mean field methods in lattice gauge theories". Physics Reports 102 (1): 1–119. doi:10.1016/0370-1573(83)90034-0. Bibcode: 1983PhR...102....1D. https://dx.doi.org/10.1016/0370-1573%2883%2990034-0.
- ↑ Lautrup, B.E.; Nauenberg, M. (1980). "Phase Transition in Four-Dimensional Compact QED". Phys. Lett. B 95 (1): 63–66. doi:10.1016/0370-2693(80)90400-1. Bibcode: 1980PhLB...95...63L. https://cds.cern.ch/record/133835.
- ↑ Guth, A.H. (1980). "Existence proof of a nonconfining phase in four-dimensional U(1) lattice gauge theory". Phys. Rev. D 21 (8): 2291–2307. doi:10.1103/PhysRevD.21.2291. Bibcode: 1980PhRvD..21.2291G. https://link.aps.org/doi/10.1103/PhysRevD.21.2291.
- ↑ Migdal, A.A. (1983). "Loop Equations and 1/N Expansion". Phys. Rep. 102 (4): 199–290. doi:10.1016/0370-1573(83)90076-5.
- ↑ Makeenko, Y.M.; Migdal, A.A. (1979). "Exact Equation for the Loop Average in Multicolor QCD". Phys. Lett. B 88 (1–2): 135–137. doi:10.1016/0370-2693(79)90131-X. Bibcode: 1979PhLB...88..135M.
- ↑ Năstase, H. (2019). "50". Introduction to Quantum Field Theory. Cambridge University Press. pp. 469–472. ISBN 978-1108493994.
- ↑ Kazakov, V.A.; Kostov, I.K. (1980). "Non-linear strings in two-dimensional U(∞) gauge theory". Nuclear Physics B 176 (1): 199–215. doi:10.1016/0550-3213(80)90072-3. Bibcode: 1980NuPhB.176..199K. https://dx.doi.org/10.1016/0550-3213%2880%2990072-3.
- ↑ Mandelstam, S. (1968). "Feynman Rules for Electromagnetic and Yang–Mills Fields from the Gauge-Independent Field-Theoretic Formalism". Phys. Rev. 175 (5): 1580–1603. doi:10.1103/PhysRev.175.1580. Bibcode: 1968PhRv..175.1580M. https://link.aps.org/doi/10.1103/PhysRev.175.1580.
- ↑ Gambini, R. (2008). "3". Loops, Knots, Gauge Theories. pp. 63–67. ISBN 978-0521654753.
- ↑ Korchemskaya, I.A.; Korchemsky, G.P. (1992). "On light-like Wilson loops". Physics Letters B 287 (1): 169–175. doi:10.1016/0370-2693(92)91895-G. Bibcode: 1992PhLB..287..169K. https://dx.doi.org/10.1016/0370-2693%2892%2991895-G.
- ↑ Polyakov, A.M. (1980). "Gauge fields as rings of glue". Nuclear Physics B 164: 171–188. doi:10.1016/0550-3213(80)90507-6. Bibcode: 1980NuPhB.164..171P. https://dx.doi.org/10.1016/0550-3213%2880%2990507-6.
- ↑ Brandt, R.A.; Neri, F.; Sato, M. (1981). "Renormalization of loop functions for all loops". Phys. Rev. D 24 (4): 879–902. doi:10.1103/PhysRevD.24.879. Bibcode: 1981PhRvD..24..879B. https://link.aps.org/doi/10.1103/PhysRevD.24.879.
- ↑ Korchemsky, G.P.; Radyushkin, A.V. (1987). "Renormalization of the Wilson loops beyond the leading order". Nuclear Physics B 283: 342–364. doi:10.1016/0550-3213(87)90277-X. Bibcode: 1987NuPhB.283..342K. https://dx.doi.org/10.1016/0550-3213%2887%2990277-X.
- ↑ Alday, L.F.; Radu, R. (2008). "Scattering Amplitudes, Wilson Loops and the String/Gauge Theory Correspondence". Phys. Rep. 468 (5): 153–211. doi:10.1016/j.physrep.2008.08.002. Bibcode: 2008PhR...468..153A.
- ↑ Alday, L.F.; Maldacena, J.M. (2007). "Gluon scattering amplitudes at strong coupling". JHEP 6 (6): 64. doi:10.1088/1126-6708/2007/06/064. Bibcode: 2007JHEP...06..064A.
- ↑ Henn, J.M. (2014). "4". Scattering Amplitudes in Gauge Theories. Springer. pp. 153–158. ISBN 978-3642540219.
- ↑ Caron-Huot, S. (2011). "Notes on the scattering amplitudes/Wilson loop duality". JHEP 2011 (7): 58. doi:10.1007/JHEP07(2011)058. Bibcode: 2011JHEP...07..058C.
- ↑ Polchinski, J. (1998). "8". String Theory Volume I: An Introduction to the Bosonic String. Cambridge University Press. pp. 263–268. ISBN 978-0143113799.
- ↑ Ibanez, L.E.; Nilles, H.P.; Quevedo, F. (1986). "Orbifolds and Wilson Lines". Phys. Lett. B 187 (1–2): 25–32. doi:10.1016/0370-2693(87)90066-9. https://cds.cern.ch/record/173902.
- ↑ Polchinski, J. (1998). "16". String Theory Volume II: Superstring Theory and Beyond. Cambridge University Press. pp. 288–290. ISBN 978-1551439761.
- ↑ Choi, K.S.; Kim, J.E. (2020). Quarks and Leptons From Orbifolded Superstring (2 ed.). ISBN 978-3030540043.
- ↑ Fradkin, E. (2021). "22". Quantum Field Theory: An Integrated Approach. Princeton University Press. p. 697. ISBN 978-0691149080.
- ↑ Witten, E. (1989). "Quantum Field Theory and the Jones Polynomial". Commun. Math. Phys. 121 (3): 351–399. doi:10.1007/BF01217730. Bibcode: 1989CMaPh.121..351W. http://projecteuclid.org/euclid.cmp/1104178138.
 |

