Physics:Nucleon magnetic moment

From HandWiki
Revision as of 04:46, 5 February 2024 by Rtextdoc (talk | contribs) (linkage)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: In physics, proton and neutron magnetism


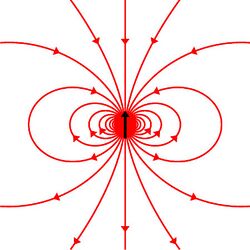
The nucleon magnetic moments are the intrinsic magnetic dipole moments of the proton and neutron, symbols μp and μn. The nucleus of an atom comprises protons and neutrons, both nucleons that behave as small magnets. Their magnetic strengths are measured by their magnetic moments. The nucleons interact with normal matter through either the nuclear force or their magnetic moments, with the charged proton also interacting by the Coulomb force.

The proton's magnetic moment, surprisingly large, was directly measured in 1933 by Otto Stern team in University of Hamburg. While the neutron was determined to have a magnetic moment by indirect methods in the mid 1930s, Luis Alvarez and Felix Bloch made the first accurate, direct measurement of the neutron's magnetic moment in 1940. The proton's magnetic moment is exploited to make measurements of molecules by proton nuclear magnetic resonance. The neutron's magnetic moment is exploited to probe the atomic structure of materials using scattering methods and to manipulate the properties of neutron beams in particle accelerators.

The existence of the neutron's magnetic moment and the large value for the proton magnetic moment indicate that nucleons are not elementary particles. For an elementary particle to have an intrinsic magnetic moment, it must have both spin and electric charge. The nucleons have spin ħ/2, but the neutron has no net charge. Their magnetic moments were puzzling and defied a valid explanation until the quark model for hadron particles was developed in the 1960s. The nucleons are composed of three quarks, and the magnetic moments of these elementary particles combine to give the nucleons their magnetic moments.

Description

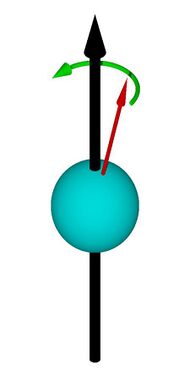
Schematic diagram depicting the spin of the neutron as the black arrow and magnetic field lines associated with the neutron's magnetic moment. The spin of the neutron is upward in this diagram, but the magnetic field lines at the center of the dipole are downward.

The CODATA recommended value for the magnetic moment of the proton is  = , or  = . The best available measurement for the value of the magnetic moment of the neutron is  = .[1] Here, μN is the nuclear magneton, a standard unit for the magnetic moments of nuclear components, and μB is the Bohr magneton, both being physical constants. In SI units, these values are  =  and  = . A magnetic moment is a vector quantity, and the direction of the nucleon's magnetic moment is determined by its spin.[2]:{{{1}}} The torque on the neutron that results from an external magnetic field is towards aligning the neutron's spin vector opposite to the magnetic field vector.[3]:{{{1}}}

The nuclear magneton is the spin magnetic moment of a Dirac particle, a charged, spin-1/2 elementary particle, with a proton's mass mp, in which anomalous corrections are ignored.[3]:{{{1}}} The nuclear magneton is [math]\displaystyle{ \mu_\text{N} = \frac{e \hbar}{2 m_\text{p}}, }[/math] where e is the elementary charge, and ħ is the reduced Planck constant.[4] The magnetic moment of such a particle is parallel to its spin.[3]:{{{1}}} Since the neutron has no charge, it should have no magnetic moment by the analogous expression.[3]:{{{1}}} The non-zero magnetic moment of the neutron thus indicates that it is not an elementary particle.[5] The sign of the neutron's magnetic moment is that of a negatively charged particle. Similarly, that the magnetic moment of the proton,  ≈ Error in {{val}}: parameter 1 is not a valid number. is not almost equal to 1 μN indicates that it too is not an elementary particle.[4] Protons and neutrons are composed of quarks, and the magnetic moments of the quarks can be used to compute the magnetic moments of the nucleons.[6]

Although the nucleons interact with normal matter through magnetic forces, the magnetic interactions are many orders of magnitude weaker than the nuclear interactions.[7] The influence of the neutron's magnetic moment is therefore only apparent for low energy, or slow, neutrons.[7] Because the value for the magnetic moment is inversely proportional to particle mass, the nuclear magneton is about 1/2000 as large as the Bohr magneton. The magnetic moment of the electron is therefore about 1000 times larger than that of the nucleons.[8]

The magnetic moments of the antiproton and antineutron have the same magnitudes as their antiparticles, the proton and neutron, but they have opposite sign.[9]

Measurement

Proton

The magnetic moment of the proton was discovered in 1933 by Otto Stern, Otto Robert Frisch and Immanuel Estermann at the University of Hamburg.[10][11][12] The proton's magnetic moment was determined by measuring the deflection of a beam of molecular hydrogen by a magnetic field.[13] Stern won the Nobel Prize in Physics in 1943 for this discovery.[14]

Neutron

The neutron was discovered in 1932,[15] and since it had no charge, it was assumed to have no magnetic moment. Indirect evidence suggested that the neutron had a non-zero value for its magnetic moment,[16] however, until direct measurements of the neutron's magnetic moment in 1940 resolved the issue.[17]

Values for the magnetic moment of the neutron were independently determined by R. Bacher[18] at the University of Michigan at Ann Arbor (1933) and I. Y. Tamm and S. A. Altshuler[19] in the Soviet Union (1934) from studies of the hyperfine structure of atomic spectra. Although Tamm and Altshuler's estimate had the correct sign and order of magnitude (μn = −0.5 μN), the result was met with skepticism.[16][2]:73–75

By 1934 groups led by Stern, now at the Carnegie Institute of Technology in Pittsburgh, and I. I. Rabi at Columbia University in New York City had independently measured the magnetic moments of the proton and deuteron.[20][21][22] The measured values for these particles were only in rough agreement between the groups, but the Rabi group confirmed the earlier Stern measurements that the magnetic moment for the proton was unexpectedly large.[16][23] Since a deuteron is composed of a proton and a neutron with aligned spins, the neutron's magnetic moment could be inferred by subtracting the deuteron and proton magnetic moments.[24] The resulting value was not zero and had a sign opposite to that of the proton. By the late 1930s, accurate values for the magnetic moment of the neutron had been deduced by the Rabi group using measurements employing newly developed nuclear magnetic resonance techniques.[23]

The value for the neutron's magnetic moment was first directly measured by L. Alvarez and F. Bloch at the University of California at Berkeley in 1940.[17] Using an extension of the magnetic resonance methods developed by Rabi, Alvarez and Bloch determined the magnetic moment of the neutron to be μn = −1.93(2) μN. By directly measuring the magnetic moment of free neutrons, or individual neutrons free of the nucleus, Alvarez and Bloch resolved all doubts and ambiguities about this anomalous property of neutrons.[25]

Unexpected consequences

The large value for the proton's magnetic moment and the inferred negative value for the neutron's magnetic moment were unexpected and could not be explained.[16] The unexpected values for the magnetic moments of the nucleons would remain a puzzle until the quark model was developed in the 1960s.[26]

The refinement and evolution of the Rabi measurements led to the discovery in 1939 that the deuteron also possessed an electric quadrupole moment.[23][27] This electrical property of the deuteron had been interfering with the measurements by the Rabi group.[23] The discovery meant that the physical shape of the deuteron was not symmetric, which provided valuable insight into the nature of the nuclear force binding nucleons.[23] Rabi was awarded the Nobel Prize in 1944 for his resonance method for recording the magnetic properties of atomic nuclei.[28]

Nucleon gyromagnetic ratios

The magnetic moment of a nucleon is sometimes expressed in terms of its g-factor, a dimensionless scalar. The convention defining the g-factor for composite particles, such as the neutron or proton, is [math]\displaystyle{ \boldsymbol{\mu} = \frac{g \mu_\text{N}}{\hbar} \boldsymbol{I}, }[/math] where μ is the intrinsic magnetic moment, I is the spin angular momentum, and g is the effective g-factor.[29] While the g-factor is dimensionless, for composite particles it is defined relative to the nuclear magneton. For the neutron, I is 1/2 ħ, so the neutron's g-factor is  = , while the proton's g-factor is gp = 5.5856946893(16).[30]

The gyromagnetic ratio, symbol γ, of a particle or system is the ratio of its magnetic moment to its spin angular momentum, or [math]\displaystyle{ \boldsymbol{\mu} = \gamma \boldsymbol{I}. }[/math]

For nucleons, the ratio is conventionally written in terms of the proton mass and charge, by the formula

[math]\displaystyle{ \gamma = \frac{g \mu_\text{N}}{\hbar} = g \frac{e}{2m_\text{p}}. }[/math]

The neutron's gyromagnetic ratio is  = . The proton's gyromagnetic ratio is  = . The gyromagnetic ratio is also the ratio between the observed angular frequency of Larmor precession and the strength of the magnetic field in nuclear magnetic resonance applications,[31] such as in MRI imaging. For this reason, the quantity γ/2π with the unit MHz/T is often given. The quantities γn/(2π) = −29.1646931(69) MHz/T[32] and γp/(2π) = 42.5774806(10) MHz⋅T−1,[33] called "gamma bar", are therefore convenient.[34]

Physical significance

Direction of Larmor precession for a neutron. The central arrow denotes the magnetic field, the small red arrow the spin of the neutron.

Larmor precession

Main page: Physics:Larmor precession

When a nucleon is put into a magnetic field produced by an external source, it is subject to a torque tending to orient its magnetic moment parallel to the field (in the case of the neutron, its spin is antiparallel to the field).[35] As with any magnet, this torque is proportional the product of the magnetic moment and the external magnetic field strength. Since the nucleons have spin angular momentum, this torque will cause them to precess with a well-defined frequency, called the Larmor frequency. It is this phenomenon that enables the measurement of nuclear properties through nuclear magnetic resonance. The Larmor frequency can be determined from the product of the gyromagnetic ratio with the magnetic field strength. Since for the neutron the sign of γn is negative, the neutron's spin angular momentum precesses counterclockwise about the direction of the external magnetic field.[36]

Proton nuclear magnetic resonance

Main page: Physics:Proton nuclear magnetic resonance

Nuclear magnetic resonance employing the magnetic moments of protons is used for nuclear magnetic resonance (NMR) spectroscopy.[37] Since hydrogen-1 nuclei are within the molecules of many substances, NMR can determine the structure of those molecules.[38]

Determination of neutron spin

The interaction of the neutron's magnetic moment with an external magnetic field was exploited to determine the spin of the neutron.[39] In 1949, D. Hughes and M. Burgy measured neutrons reflected from a ferromagnetic mirror and found that the angular distribution of the reflections was consistent with spin 1/2.[40] In 1954, J. Sherwood, T. Stephenson, and S. Bernstein employed neutrons in a Stern–Gerlach experiment that used a magnetic field to separate the neutron spin states.[41] They recorded the two such spin states, consistent with a spin 1/2 particle.[41][39] Until these measurements, the possibility that the neutron was a spin 3/2 particle could not have been ruled out.[39]

Neutrons used to probe material properties

Since neutrons are neutral particles, they do not have to overcome Coulomb repulsion as they approach charged targets, unlike protons and alpha particles.[7] Neutrons can deeply penetrate matter.[7] The magnetic moment of the neutron has therefore been exploited to probe the properties of matter using scattering or diffraction techniques.[7] These methods provide information that is complementary to X-ray spectroscopy.[7][38] In particular, the magnetic moment of the neutron is used to determine magnetic properties of materials at length scales of 1–100 Å using cold or thermal neutrons.[42] B. Brockhouse and C. Shull won the Nobel Prize in physics in 1994 for developing these scattering techniques.[43]

Control of neutron beams by magnetism

As neutrons carry no electric charge, neutron beams cannot be controlled by the conventional electromagnetic methods employed in particle accelerators.[44] The magnetic moment of the neutron allows some control of neutrons using magnetic fields, however, including the formation of polarized neutron beams.[45][44] One technique employs the fact that cold neutrons will reflect from some magnetic materials at great efficiency when scattered at small grazing angles.[46] The reflection preferentially selects particular spin states, thus polarizing the neutrons. Neutron magnetic mirrors and guides use this total internal reflection phenomenon to control beams of slow neutrons.[47]

Nuclear magnetic moments

Main page: Physics:Nuclear magnetic moment

Since an atomic nucleus consists of a bound state of protons and neutrons, the magnetic moments of the nucleons contribute to the nuclear magnetic moment, or the magnetic moment for the nucleus as a whole.[39] The nuclear magnetic moment also includes contributions from the orbital motion of the charged protons.[39] The deuteron, consisting of a proton and a neutron, has the simplest example of a nuclear magnetic moment.[39] The sum of the proton and neutron magnetic moments gives 0.879 µN, which is within 3% of the measured value 0.857 µN.[48] In this calculation, the spins of the nucleons are aligned, but their magnetic moments offset because of the neutron's negative magnetic moment.[48]

Nature of the nucleon magnetic moments

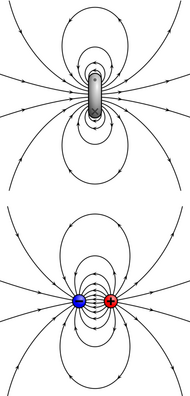
A magnetic dipole moment can be created by either a current loop (top; Ampèrian) or by two magnetic monopoles (bottom; Gilbertian). The nucleon magnetic moments are Ampèrian.

A magnetic dipole moment can be generated by two possible mechanisms.[49] One way is by a small loop of electric current, called an "Ampèrian" magnetic dipole. Another way is by a pair of magnetic monopoles of opposite magnetic charge, bound together in some way, called a "Gilbertian" magnetic dipole. Elementary magnetic monopoles remain hypothetical and unobserved, however. Throughout the 1930s and 1940s it was not readily apparent which of these two mechanisms caused the nucleon intrinsic magnetic moments. In 1930, Enrico Fermi showed that the magnetic moments of nuclei (including the proton) are Ampèrian.[50] The two kinds of magnetic moments experience different forces in a magnetic field. Based on Fermi's arguments, the intrinsic magnetic moments of elementary particles, including the nucleons, have been shown to be Ampèrian. The arguments are based on basic electromagnetism, elementary quantum mechanics, and the hyperfine structure of atomic s-state energy levels.[51] In the case of the neutron, the theoretical possibilities were resolved by laboratory measurements of the scattering of slow neutrons from ferromagnetic materials in 1951.[49][52][53][54]

Anomalous magnetic moments and meson physics

The anomalous values for the magnetic moments of the nucleons presented a theoretical quandary for the 30 years from the time of their discovery in the early 1930s to the development of the quark model in the 1960s.[26] Considerable theoretical efforts were expended in trying to understand the origins of these magnetic moments, but the failures of these theories were glaring.[26] Much of the theoretical focus was on developing a nuclear-force equivalence to the remarkably successful theory explaining the small anomalous magnetic moment of the electron.[26]

The problem of the origins of the magnetic moments of nucleons was recognized as early as 1935. G. C. Wick suggested that the magnetic moments could be caused by the quantum-mechanical fluctuations of these particles in accordance with Fermi's 1934 theory of beta decay.[55] By this theory, a neutron is partly, regularly and briefly, disassociated into a proton, an electron, and a neutrino as a natural consequence of beta decay.[56] By this idea, the magnetic moment of the neutron was caused by the fleeting existence of the large magnetic moment of the electron in the course of these quantum-mechanical fluctuations, the value of the magnetic moment determined by the length of time the virtual electron was in existence.[57] The theory proved to be untenable, however, when H. Bethe and R. Bacher showed that it predicted values for the magnetic moment that were either much too small or much too large, depending on speculative assumptions.[55][58]

Similar considerations for the electron proved to be much more successful. In quantum electrodynamics (QED), the anomalous magnetic moment of a particle stems from the small contributions of quantum mechanical fluctuations to the magnetic moment of that particle.[59] The g-factor for a "Dirac" magnetic moment is predicted to be g = −2 for a negatively charged, spin-1/2 particle. For particles such as the electron, this "classical" result differs from the observed value by around 0.1%; the difference compared to the classical value is the anomalous magnetic moment. The g-factor for the electron is measured to be −2.00231930436256(35).[60] QED is the theory of the mediation of the electromagnetic force by photons. The physical picture is that the effective magnetic moment of the electron results from the contributions of the "bare" electron, which is the Dirac particle, and the cloud of "virtual", short-lived electron–positron pairs and photons that surround this particle as a consequence of QED. The effects of these quantum mechanical fluctuations can be computed theoretically using Feynman diagrams with loops.[61]

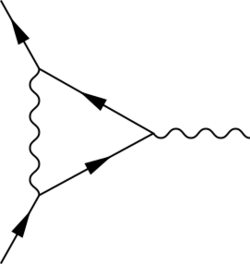
One-loop correction to a fermion's magnetic dipole moment. The solid lines at top and bottom represent the fermion (electron or nucleon), the wavy lines represent the particle mediating the force (photons for QED, mesons for nuclear force). The middle solid lines represent a virtual pair of particles (electron and positron for QED, pions for the nuclear force).

The one-loop contribution to the anomalous magnetic moment of the electron, corresponding to the first-order and largest correction in QED, is found by calculating the vertex function shown in the diagram on the right. The calculation was discovered by J. Schwinger in 1948.[59][62] Computed to fourth order, the QED prediction for the electron's anomalous magnetic moment agrees with the experimentally measured value to more than 10 significant figures, making the magnetic moment of the electron one of the most accurately verified predictions in the history of physics.[59]

Compared to the electron, the anomalous magnetic moments of the nucleons are enormous.[5] The g-factor for the proton is 5.6, and the chargeless neutron, which should have no magnetic moment at all, has a g-factor of −3.8. Note, however, that the anomalous magnetic moments of the nucleons, that is, their magnetic moments with the expected Dirac particle magnetic moments subtracted, are roughly equal but of opposite sign: μp − 1.00 μN = +1.79 μN, but μn − 0.00 μN = −1.91 μN.[63]

The Yukawa interaction for nucleons was discovered in the mid-1930s, and this nuclear force is mediated by pion mesons.[55] In parallel with the theory for the electron, the hypothesis was that higher-order loops involving nucleons and pions may generate the anomalous magnetic moments of the nucleons.[4] The physical picture was that the effective magnetic moment of the neutron arose from the combined contributions of the "bare" neutron, which is zero, and the cloud of "virtual" pions and photons that surround this particle as a consequence of the nuclear and electromagnetic forces.[2]:75–80[64] The Feynman diagram at right is roughly the first-order diagram, with the role of the virtual particles played by pions. As noted by A. Pais, "between late 1948 and the middle of 1949 at least six papers appeared reporting on second-order calculations of nucleon moments".[26] These theories were also, as noted by Pais, "a flop" – they gave results that grossly disagreed with observation. Nevertheless, serious efforts continued along these lines for the next couple of decades, to little success.[4][64][65] These theoretical approaches were incorrect because the nucleons are composite particles with their magnetic moments arising from their elementary components, quarks.[26]

Quark model of nucleon magnetic moments

In the quark model for hadrons, the neutron is composed of one up quark (charge ++ 2 /3 e) and two down quarks (charge −+ 1 /3 e) while the proton is composed of one down quark (charge −+ 1 /3 e) and two up quarks (charge ++ 2 /3 e).[66] The magnetic moment of the nucleons can be modeled as a sum of the magnetic moments of the constituent quarks,[6] although this simple model belies the complexities of the Standard Model of Particle Physics.[67] The calculation assumes that the quarks behave like pointlike Dirac particles, each having their own magnetic moment, as computed using an expression similar to the one above for the nuclear magneton: [math]\displaystyle{ \ \mu_\text{q} = \frac{\ e_\text{q} \hbar\ }{2 m_\text{q}}\ , }[/math] where the q-subscripted variables refer to quark magnetic moment, charge, or mass.[6] Simplistically, the magnetic moment of a nucleon can be viewed as resulting from the vector sum of the three quark magnetic moments, plus the orbital magnetic moments caused by the movement of the three charged quarks within it.[6]

In one of the early successes of the Standard Model (SU(6) theory), in 1964 M. Beg, B. Lee, and A. Pais theoretically calculated the ratio of proton-to-neutron magnetic moments to be −+3/ 2 , which agrees with the experimental value to within 3%.[68][69][70] The measured value for this ratio is −1.45989806(34).[71] A contradiction of the quantum mechanical basis of this calculation with the Pauli exclusion principle led to the discovery of the color charge for quarks by O. Greenberg in 1964.[68]

From the nonrelativistic quantum-mechanical wave function for baryons composed of three quarks, a straightforward calculation gives fairly accurate estimates for the magnetic moments of neutrons, protons, and other baryons.[6] For a neutron, the magnetic moment is given by μn =  4 /3 μd −  1 /3 μu , where μd and μu are the magnetic moments for the down and up quarks respectively. This result combines the intrinsic magnetic moments of the quarks with their orbital magnetic moments and assumes that the three quarks are in a particular, dominant quantum state.[6]

Baryon Magnetic moment
of quark model 		Computed
([math]\displaystyle{ \mu_\text{N} }[/math]) 		Observed
([math]\displaystyle{ \mu_\text{N} }[/math])
p  4 /3 μu −  1 /3 μd 2.79 2.793
n  4 /3 μd −  1 /3 μu −1.86 −1.913

The results of this calculation are encouraging, but the masses of the up or down quarks were assumed to be  1 /3 the mass of a nucleon.[6] The masses of the quarks are actually only about 1% that of a nucleon. The discrepancy stems from the complexity of the Standard Model for nucleons, where most of their mass originates in the gluon fields, virtual particles, and their associated energy that are essential aspects of the strong force.[67][72] Furthermore, the complex system of quarks and gluons that constitute a nucleon requires a relativistic treatment.[73] Nucleon magnetic moments have been successfully computed from first principles, requiring significant computing resources.[74][75]

See also

References

  1. ↑ Beringer, J. (2012). "Review of Particle Physics, 2013 partial update". Phys. Rev. D 86 (1): 010001. doi:10.1103/PhysRevD.86.010001. Bibcode: 2012PhRvD..86a0001B. http://pdg.lbl.gov/2013/listings/rpp2013-list-n.pdf. Retrieved May 8, 2015. 
  2. ↑ 2.0 2.1 2.2 Vonsovsky, Sergei (1975). Magnetism of Elementary Particles. Moscow: Mir Publishers. https://archive.org/details/MagnetismOfElementaryParticles. 
  3. ↑ 3.0 3.1 3.2 3.3 Shankar, R. (1994). Principles of Quantum Mechanics (2nd ed.). Kluwer Academic/Plenum Press. pp. 676. doi:10.1007/978-1-4757-0576-8. ISBN 978-1-4757-0576-8. https://link.springer.com/book/10.1007/978-1-4757-0576-8. 
  4. ↑ 4.0 4.1 4.2 4.3 Bjorken, J. D.; Drell, S. D. (1964). Relativistic Quantum Mechanics. New York: McGraw-Hill. pp. 241–246. ISBN 978-0070054936. https://archive.org/details/relativisticquan0000bjor. 
  5. ↑ 5.0 5.1 Hausser, O. (1981). "Nuclear Moments". in Lerner, R. G.; Trigg, G. L.. Encyclopedia of Physics. Reading, Massachusetts: Addison-Wesley Publishing Company. pp. 679–680. ISBN 978-0201043136. 
  6. ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Introduction to High Energy Physics. Reading, Massachusetts: Addison Wesley. 1982. pp. 201–202. ISBN 978-0-201-05757-7. https://archive.org/details/introductiontohi0000perk. 
  7. ↑ 7.0 7.1 7.2 7.3 7.4 7.5 Snow, M. (2013). "Exotic physics with slow neutrons". Physics Today 66 (3): 50–55. doi:10.1063/PT.3.1918. Bibcode: 2013PhT....66c..50S. https://physicstoday.scitation.org/doi/full/10.1063/PT.3.1918. Retrieved December 11, 2015. 
  8. ↑ "CODATA values of the fundamental constants". NIST. http://physics.nist.gov/cgi-bin/cuu/Value?muemsmunn. 
  9. ↑ Schreckenbach, K. (2013). "Physics of the Neutron". in Stock, R.. Encyclopedia of Nuclear Physics and its Applications. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co.. pp. 321–354. ISBN 978-3-527-40742-2. 
  10. ↑ Frisch, R.; Stern, O. (1933). "Über die magnetische Ablenkung von Wasserstoffmolekülen und das magnetische Moment des Protons. I / Magnetic Deviation of Hydrogen Molecules and the Magnetic Moment of the Proton. I". Z. Phys. 85 (1–2): 4–16. doi:10.1007/bf01330773. Bibcode: 1933ZPhy...85....4F. http://web.ihep.su/owa/dbserv/hw.part2?s_c=FRISCH+1933. 
  11. ↑ Esterman, I.; Stern, O. (1933). "Über die magnetische Ablenkung von Wasserstoffmolekülen und das magnetische Moment des Protons. II / Magnetic Deviation of Hydrogen Molecules and the Magnetic Moment of the Proton. I". Z. Phys. 85 (1–2): 17–24. doi:10.1007/bf01330774. Bibcode: 1933ZPhy...85...17E. http://web.ihep.su/owa/dbserv/hw.part2?s_c=FRISCH+1933. 
  12. ↑ Ramsey, N. F. (1988-06-01). "Molecular beams: our legacy from Otto Stern" (in en). Zeitschrift für Physik D Atoms, Molecules and Clusters 10 (2): 121–125. doi:10.1007/BF01384845. ISSN 1431-5866. Bibcode: 1988ZPhyD..10..121R. https://doi.org/10.1007/BF01384845. 
  13. ↑ Toennies, J. P.; Schmidt-Bocking, H.; Friedrich, B.; Lower, J. C. A. (2011). "Otto Stern (1888–1969): The founding father of experimental atomic physics". Annalen der Physik 523 (12): 1045–1070. doi:10.1002/andp.201100228. Bibcode: 2011AnP...523.1045T. 
  14. ↑ "The Nobel Prize in Physics 1943". Nobel Foundation. https://www.nobelprize.org/nobel_prizes/physics/laureates/1943/. 
  15. ↑ Chadwick, James (1932). "Existence of a Neutron". Proceedings of the Royal Society A 136 (830): 692–708. doi:10.1098/rspa.1932.0112. Bibcode: 1932RSPSA.136..692C. 
  16. ↑ 16.0 16.1 16.2 16.3 Breit, G.; Rabi, I. I. (1934). "On the interpretation of present values of nuclear moments". Physical Review 46 (3): 230–231. doi:10.1103/physrev.46.230. Bibcode: 1934PhRv...46..230B. 
  17. ↑ 17.0 17.1 Alvarez, L. W.; Bloch, F. (1940). "A quantitative determination of the neutron magnetic moment in absolute nuclear magnetons". Physical Review 57 (2): 111–122. doi:10.1103/physrev.57.111. Bibcode: 1940PhRv...57..111A. 
  18. ↑ Bacher, R. F. (1933). "Note on the Magnetic Moment of the Nitrogen Nucleus". Physical Review 43 (12): 1001–1002. doi:10.1103/physrev.43.1001. Bibcode: 1933PhRv...43.1001B. https://authors.library.caltech.edu/51310/1/PhysRev.43.1001.pdf. 
  19. ↑ Tamm, I. Y.; Altshuler, S. A. (1934). "Magnetic moment of the neutron". Doklady Akademii Nauk SSSR 8: 455. http://web.ihep.su/owa/dbserv/hw.part2?s_c=ALTSHULER+1934. Retrieved 2015-01-30. 
  20. ↑ Esterman, I.; Stern, O. (1934). "Magnetic moment of the deuton". Physical Review 45 (10): 761(A109). doi:10.1103/PhysRev.45.739. Bibcode: 1934PhRv...45..739S. http://web.ihep.su/owa/dbserv/hw.part2?s_c=ESTERMAN+1934. Retrieved 9 May 2015. 
  21. ↑ Rabi, I. I.; Kellogg, J. M.; Zacharias, J. R. (1934). "The magnetic moment of the proton". Physical Review 46 (3): 157–163. doi:10.1103/physrev.46.157. Bibcode: 1934PhRv...46..157R. 
  22. ↑ Rabi, I. I.; Kellogg, J. M.; Zacharias, J. R. (1934). "The magnetic moment of the deuton". Physical Review 46 (3): 163–165. doi:10.1103/physrev.46.163. Bibcode: 1934PhRv...46..163R. 
  23. ↑ 23.0 23.1 23.2 23.3 23.4 Rigden, John S. (1987). Rabi, Scientist and Citizen. New York: Basic Books, Inc.. pp. 99–114. ISBN 9780674004351. https://books.google.com/books?id=Qgv9Xjv8_LYC&q=rabi+kellogg+zacharias+magnetic+moment+neutron&pg=PA106. Retrieved 9 May 2015. 
  24. ↑ J. Rigden (November 1, 1999). "Isidor Isaac Rabi: walking the path of God". Physics World. https://physicsworld.com/a/isidor-isaac-rabi-walking-the-path-of-god/. 
  25. ↑ Ramsey, Norman F. (1987). "Chapter 5: The Neutron Magnetic Moment". in Trower, W. Peter. Discovering Alvarez: Selected works of Luis W. Alvarez with commentary by his students and colleagues. University of Chicago Press. pp. 30–32. ISBN 978-0226813042. https://books.google.com/books?id=imidr-iFYCwC&q=alvarez+and+bloch+magnetic+moment&pg=PA31. Retrieved 9 May 2015. 
  26. ↑ 26.0 26.1 26.2 26.3 26.4 26.5 Pais, Abraham (1986). Inward Bound. Oxford: Oxford University Press. p. 299. ISBN 978-0198519973. https://archive.org/details/inwardboundofmat00pais_0. 
  27. ↑ Kellogg, J. M.; Rabi, I. I.; Ramsey, N. F.; Zacharias, J. R. (1939). "An electrical quadrupole moment of the deuteron". Physical Review 55 (3): 318–319. doi:10.1103/physrev.55.318. Bibcode: 1939PhRv...55..318K. 
  28. ↑ "The Nobel Prize in Physics 1944". Nobel Foundation. https://www.nobelprize.org/nobel_prizes/physics/laureates/1944/. 
  29. ↑ Povh, B.; Rith, K.; Scholz, C.; Zetsche, F. (2002). Particles and Nuclei: An Introduction to the Physical Concepts. Berlin: Springer-Verlag. pp. 74–75, 259–260. ISBN 978-3-540-43823-6. https://books.google.com/books?id=HC_qCAAAQBAJ&pg=PA389. Retrieved 10 May 2015. 
  30. ↑ "2018 CODATA Value: proton g factor". The NIST Reference on Constants, Units, and Uncertainty. NIST. June 2015. http://physics.nist.gov/cgi-bin/cuu/Value?gp. Retrieved 2019-03-08. 
  31. ↑ Jacobsen, Neil E. (2007). NMR spectroscopy explained. Hoboken, New Jersey: Wiley-Interscience. ISBN 9780471730965. http://books.scholarsportal.info/viewdoc.html?id=/ebooks/ebooks2/wiley/2011-12-13/1/9780470173350. Retrieved May 8, 2015. 
  32. ↑ "CODATA values of the fundamental constants". NIST. http://physics.nist.gov/cgi-bin/cuu/Value?gammanbar. 
  33. ↑ "CODATA values of the fundamental constants". NIST. http://physics.nist.gov/cgi-bin/cuu/Value?gammapbar. 
  34. ↑ Berry, E.; Bulpitt, A. J. (2008). Fundamentals of MRI: An Interactive Learning Approach. Boca Raton, Florida: CRC Press. pp. 320. ISBN 9781584889021. https://books.google.com/books?id=oLPNBQAAQBAJ&dq=%22gamma+bar%22+gyromagnetic+ratio&pg=PA47. Retrieved December 12, 2022. 
  35. ↑ B. D. Cullity; C. D. Graham (2008). Introduction to Magnetic Materials (2nd ed.). Hoboken, New Jersey: Wiley-IEEE Press. p. 103. ISBN 978-0-471-47741-9. https://books.google.com/books?id=ixAe4qIGEmwC&pg=PA103. Retrieved May 8, 2015. 
  36. ↑ M. H. Levitt (2001). Spin dynamics: basics of nuclear magnetic resonance. West Sussex, England: John Wiley & Sons. pp. 25–30. ISBN 978-0-471-48921-4. https://archive.org/details/isbn_9780471489221. 
  37. ↑ Balci, M. (2005). Basic 1H- and 13C-NMR Spectroscopy (1st ed.). Amsterdam: Elsevier. pp. 1–7. ISBN 978-0444518118. https://www.elsevier.com/books/basic-1h-and-13c-nmr-spectroscopy/balci/978-0-444-51811-8. Retrieved December 12, 2022. 
  38. ↑ 38.0 38.1 R. M. Silverstein; F. X. Webster; D. J. Kiemle; D. L. Bryce (2014). Spectrometric Identification of Organic Compounds (8th ed.). Hoboken, New Jersey: Wiley. pp. 126–163. ISBN 978-0-470-61637-6. https://www.wiley.com/en-ie/Spectrometric+Identification+of+Organic+Compounds,+8th+Edition-p-9780470616376. Retrieved December 10, 2022. 
  39. ↑ 39.0 39.1 39.2 39.3 39.4 39.5 Byrne, J. (2011). Neutrons, Nuclei, and Matter: An exploration of the physics of slow neutrons. Mineola, NY: Dover Publications. pp. 28–31. ISBN 978-0486482385. 
  40. ↑ Hughes, D.J.; Burgy, M.T. (1949). "Reflection and polarization of neutrons by magnetized mirrors". Phys. Rev. 76 (9): 1413–1414. doi:10.1103/PhysRev.76.1413. Bibcode: 1949PhRv...76.1413H. http://physics.princeton.edu/~mcdonald/examples/EP/hughes_pr_76_1413_49.pdf. Retrieved 2016-06-26. 
  41. ↑ 41.0 41.1 Sherwood, J.E.; Stephenson, T.E.; Bernstein, S. (1954). "Stern–Gerlach experiment on polarized neutrons". Phys. Rev. 96 (6): 1546–1548. doi:10.1103/PhysRev.96.1546. Bibcode: 1954PhRv...96.1546S. 
  42. ↑ S. W. Lovesey (1986). Theory of Neutron Scattering from Condensed Matter. 1: Nuclear Scattering. Oxford: Clarendon Press. pp. 1–30. ISBN 978-0198520290. 
  43. ↑ "The Nobel Prize in Physics 1994". Nobel Foundation. https://www.nobelprize.org/nobel_prizes/physics/laureates/1994/press.html. 
  44. ↑ 44.0 44.1 Arimoto, Y. et al. (2012). "Demonstration of focusing by a neutron accelerator". Physical Review A 86 (2): 023843. doi:10.1103/PhysRevA.86.023843. Bibcode: 2012PhRvA..86b3843A. http://www.rri.kyoto-u.ac.jp/news-en/4964. Retrieved May 9, 2015. 
  45. ↑ Oku, T. et al. (2007). "Highly polarized cold neutron beam obtained by using a quadrupole magnet". Physica B 397 (1–2): 188–191. doi:10.1016/j.physb.2007.02.055. Bibcode: 2007PhyB..397..188O. 
  46. ↑ Fernandez-Alonso, Felix; Price, David (2013). Neutron Scattering Fundamentals. Amsterdam: Academic Press. pp. 103. ISBN 978-0-12-398374-9. https://books.google.com/books?id=LdlAAAAAQBAJ&q=neutron+optics+mirror+magnetic&pg=PA103. Retrieved June 30, 2016. 
  47. ↑ Chupp, T. "Neutron Optics and Polarization". https://www.ncnr.nist.gov/summerschool/ss09/pdf/Chupp_FP09.pdf. Retrieved 16 April 2019. 
  48. ↑ 48.0 48.1 Semat, Henry (1972). Introduction to Atomic and Nuclear Physics (5th ed.). London: Holt, Rinehart and Winston. pp. 556. ISBN 978-1-4615-9701-8. https://books.google.com/books?id=WJvTBwAAQBAJ&q=deuterium+magnetic+dipole+moment+sum+of+proton+and+neutron&pg=PA556. Retrieved May 8, 2015. 
  49. ↑ 49.0 49.1 McDonald, K. T. (2014). "The Forces on Magnetic Dipoles". Joseph Henry Laboratory, Princeton University. http://physics.princeton.edu/~mcdonald/examples/neutron.pdf. Retrieved 18 June 2017. 
  50. ↑ Fermi, E. (1930). "Uber die magnetischen Momente der Atomkerne" (in de). Z. Phys. 60 (5–6): 320–333. doi:10.1007/bf01339933. Bibcode: 1930ZPhy...60..320F. 
  51. ↑ Jackson, J. D. (1977). "The nature of intrinsic magnetic dipole moments". CERN 77-17: 1–25. http://physics.princeton.edu/~mcdonald/examples/EP/jackson_CERN-77-17.pdf. Retrieved 18 June 2017. 
  52. ↑ Mezei, F. (1986). "La Nouvelle Vague in Polarized Neutron Scattering". Physica 137B (1): 295–308. doi:10.1016/0378-4363(86)90335-9. Bibcode: 1986PhyBC.137..295M. 
  53. ↑ Hughes, D. J.; Burgy, M. T. (1951). "Reflection of neutrons from magnetized mirrors". Physical Review 81 (4): 498–506. doi:10.1103/physrev.81.498. Bibcode: 1951PhRv...81..498H. 
  54. ↑ Shull, C. G.; Wollan, E. O.; Strauser, W. A. (1951). "Magnetic structure of magnetite and its use in studying the neutron magnetic interaction". Physical Review 81 (3): 483–484. doi:10.1103/physrev.81.483. Bibcode: 1951PhRv...81..483S. 
  55. ↑ 55.0 55.1 55.2 Brown, L. M.; Rechenberg, H. (1996). The Origin of the Concept of Nuclear Forces. Bristol and Philadelphia: Institute of Physics Publishing. pp. 95–312. ISBN 978-0750303736. https://archive.org/details/originofconcepto0000brow. 
  56. ↑ Wick, G. C. (1935). "Teoria dei raggi beta e momento magnetico del protone". Rend. R. Accad. Lincei 21: 170–175. 
  57. ↑ Amaldi, E. (1998). "Gian Carlo Wick during the 1930s". in Battimelli, G.; Paoloni, G.. 20th Century Physics: Essays and Recollections: a Selection of Historical Writings by Edoardo Amaldi. Singapore: World Scientific Publishing Company. pp. 128–139. ISBN 978-9810223694. 
  58. ↑ Bethe, H. A.; Bacher, R. F. (1936). "Nuclear Physics A. Stationary states of nuclei". Reviews of Modern Physics 8 (5): 82–229. doi:10.1103/RevModPhys.8.82. Bibcode: 1936RvMP....8...82B. https://authors.library.caltech.edu/51288/1/RevModPhys.8.82.pdf. 
  59. ↑ 59.0 59.1 59.2 Peskin, M. E.; Schroeder, D. V. (1995). An Introduction to Quantum Field Theory. Reading, Massachusetts: Perseus Books. pp. 175–198. ISBN 978-0201503975. https://archive.org/details/introductiontoqu0000pesk/page/175. 
  60. ↑ "2018 CODATA Value: electron g factor". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?gem. Retrieved 2019-05-20. 
  61. ↑ Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. (2008). "Revised value of the eighth-order QED contribution to the anomalous magnetic moment of the electron". Physical Review D 77 (5): 053012. doi:10.1103/PhysRevD.77.053012. Bibcode: 2008PhRvD..77e3012A. 
  62. ↑ Schwinger, J. (1948). "On Quantum-Electrodynamics and the Magnetic Moment of the Electron". Physical Review 73 (4): 416–417. doi:10.1103/PhysRev.73.416. Bibcode: 1948PhRv...73..416S. 
  63. ↑ See chapter 1, section 6 in deShalit, A.; Feschbach, H. (1974). Theoretical Nuclear Physics Volume I: Nuclear Structure. New York: John Wiley and Sons. p. 31. ISBN 978-0471203858. 
  64. ↑ 64.0 64.1 Drell, S.; Zachariasen, F. (1961). Electromagnetic Structure of Nucleons. New York: Oxford University Press. pp. 1–130. https://archive.org/details/electromagnetics002214mbp. 
  65. ↑ Drell, S.; Pagels, H. R. (1965). "Anomalous Magnetic Moment of the Electron, Muon, and Nucleon". Physical Review 140 (2B): B397–B407. doi:10.1103/PhysRev.140.B397. Bibcode: 1965PhRv..140..397D. https://www.slac.stanford.edu/cgi-bin/getdoc/slac-pub-0102.pdf. 
  66. ↑ Gell, Y.; Lichtenberg, D. B. (1969). "Quark model and the magnetic moments of proton and neutron". Il Nuovo Cimento A. Series 10 61 (1): 27–40. doi:10.1007/BF02760010. Bibcode: 1969NCimA..61...27G. 
  67. ↑ 67.0 67.1 Cho, Adiran (2 April 2010). "Mass of the common quark finally nailed down". Science (American Association for the Advancement of Science). https://www.science.org/content/article/mass-common-quark-finally-nailed-down. 
  68. ↑ 68.0 68.1 Greenberg, O.W. (2009). "Color charge degree of freedom in particle physics". Compendium of Quantum Physics. Springer Berlin Heidelberg. pp. 109–111. doi:10.1007/978-3-540-70626-7_32. ISBN 978-3-540-70622-9. 
  69. ↑ Beg, M.A.B.; Lee, B.W.; Pais, A. (1964). "SU(6) and electromagnetic interactions". Physical Review Letters 13 (16): 514–517, erratum 650. doi:10.1103/physrevlett.13.514. Bibcode: 1964PhRvL..13..514B. 
  70. ↑ Sakita, B. (1964). "Electromagnetic properties of baryons in the supermultiplet scheme of elementary particles". Physical Review Letters 13 (21): 643–646. doi:10.1103/physrevlett.13.643. Bibcode: 1964PhRvL..13..643S. 
  71. ↑ The 2010 CODATA Recommended Values of the Fundamental Physical Constants (Report). Gaithersburg, MD: National Institute of Standards and Technology. 2011-06-02. Web Version 6.0. http://physics.nist.gov/constants. Retrieved 9 May 2015.  The database was developed by J. Baker, M. Douma, and S. Kotochigova.
  72. ↑ Wilczek, F. (2003). "The Origin of Mass". MIT Physics Annual: 24–35. https://physics.mit.edu/wp-content/uploads/2021/01/physicsatmit_03_wilczek_originofmass.pdf. Retrieved May 8, 2015. 
  73. ↑ Ji, Xiangdong (1995). "A QCD analysis of the mass structure of the nucleon". Phys. Rev. Lett. 74 (7): 1071–1074. doi:10.1103/PhysRevLett.74.1071. PMID 10058927. Bibcode: 1995PhRvL..74.1071J. 
  74. ↑ Martinelli, G.; Parisi, G.; Petronzio, R.; Rapuano, F. (1982). "The proton and neutron magnetic moments in lattice QCD". Physics Letters B 116 (6): 434–436. doi:10.1016/0370-2693(82)90162-9. Bibcode: 1982PhLB..116..434M. https://cds.cern.ch/record/138281/files/198207343.pdf. 
  75. ↑ Kincade, Kathy (2 February 2015). "Pinpointing the magnetic moments of nuclear matter". http://phys.org/news/2015-02-magnetic-moments-nuclear.html. 

Bibliography

  • S. W. Lovesey (1986). Theory of Neutron Scattering from Condensed Matter. Oxford University Press. ISBN:0198520298.
  • Donald H. Perkins (1982). Introduction to High Energy Physics. Reading, Massachusetts: Addison Wesley, ISBN:0-201-05757-3.
  • John S. Rigden (1987). Rabi, Scientist and Citizen. New York: Basic Books, Inc., ISBN:0-465-06792-1.
  • Sergei Vonsovsky (1975). Magnetism of Elementary Particles. Moscow: Mir Publishers.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Nucleon_magnetic_moment&oldid=3281802"