Physics:Nuclear magnetic resonance

Short description: Spectroscopic technique based on change of nuclear spin state

Bruker 700 MHz nuclear magnetic resonance (NMR) spectrometer.

File:Nuclear Magnetic Resonance (NMR) basic principles.webm

Nuclear magnetic resonance (NMR) is a physical phenomenon in which nuclei in a strong constant magnetic field are perturbed by a weak oscillating magnetic field (in the near field) and respond by producing an electromagnetic signal with a frequency characteristic of the magnetic field at the nucleus. This process occurs near resonance, when the oscillation frequency matches the intrinsic frequency of the nuclei, which depends on the strength of the static magnetic field, the chemical environment, and the magnetic properties of the isotope involved; in practical applications with static magnetic fields up to ca. 20 tesla, the frequency is similar to VHF and UHF television broadcasts (60–1000 MHz). NMR results from specific magnetic properties of certain atomic nuclei. Nuclear magnetic resonance spectroscopy is widely used to determine the structure of organic molecules in solution and study molecular physics and crystals as well as non-crystalline materials. NMR is also routinely used in advanced medical imaging techniques, such as in magnetic resonance imaging (MRI). The original application of NMR to condensed matter physics is nowadays mostly devoted to strongly correlated electron systems. It reveals large manybody couplings by fast broadband detection and it should not to be confused with solid state NMR, which aims at removing the effect of the same couplings by Magic Angle Spinning techniques.

The most commonly used nuclei are ¹H and ¹³C, although isotopes of many other elements, such as ¹⁹F, ³¹P, and³³S, can be studied by high-field NMR spectroscopy as well. In order to interact with the magnetic field in the spectrometer, the nucleus must have an intrinsic nuclear magnetic moment and angular momentum. This occurs when an isotope has a nonzero nuclear spin, meaning an odd number of protons and/or neutrons (see Isotope). Nuclides with even numbers of both have a total spin of zero and are therefore NMR-inactive.

In its application to molecules the NMR effect can be observed only in the presence of a magnetic field. However, in the ordered phase of magnetic materials very large internal fields are produced at the nuclei of magnetic ions (and of close logands), which allow NMR to be performed in zero applied field. Additionally, radiofrequency transitions of nuclear spin I > 1/2 with large enough electric quadrupolar coupling to the internal electric field gradient may also be excited in zero applied magnetic field.

In the dominant chemistry application the use of higher fields improves the sentivity of the method (signal-to-noise ratio scales approximately as the power of 3/2 with the magnetic field strength) and the spectral resolution. Commercial NMR spectrometers employing liquid helium cooled superconducting magnets with over 20 Tesla fields have been developed and are widely used.

A key feature of NMR is that the resonant frequency of a particular sample substance is usually directly proportional to the strength of the applied magnetic field. It is this feature that is exploited in imaging techniques; if a sample is placed in a non-uniform magnetic field then the resonance frequencies of the sample's nuclei depend on where in the field they are located. This effect serves as the basis of magnetic resonance imaging.

The principle of NMR usually involves three sequential steps:

• The alignment (polarization) of the magnetic nuclear spins in an applied, constant magnetic field B₀.
• The perturbation of this alignment of the nuclear spins by a weak oscillating magnetic field, usually referred to as a radio frequency (RF) pulse. The oscillation frequency required for significant perturbation is dependent upon the static magnetic field (B₀) and the nuclei of observation.
• The detection of the NMR signal during or after the RF pulse, due to the voltage induced in a detection coil by precession of the nuclear spins around B₀. After an RF pulse, precession usually occurs with the nuclei's intrinsic Larmor frequency and, in itself, does not involve transitions between spin states or energy levels.

The two magnetic fields are usually chosen to be perpendicular to each other as this maximizes the NMR signal strength. The frequencies of the time-signal response by the total magnetization (M) of the nuclear spins are analyzed in NMR spectroscopy and magnetic resonance imaging. Both use applied magnetic fields (B₀) of great strength, often produced by large currents in superconducting coils, in order to achieve dispersion of response frequencies and of very high homogeneity and stability in order to deliver spectral resolution, the details of which are described by chemical shifts, the Zeeman effect, and Knight shifts (in metals). The information provided by NMR can also be increased using hyperpolarization, and/or using two-dimensional, three-dimensional and higher-dimensional techniques.

NMR phenomena are also utilized in low-field NMR, NMR spectroscopy and MRI in the Earth's magnetic field (referred to as Earth's field NMR), and in several types of magnetometers.

History

Nuclear magnetic resonance was first described and measured in molecular beams by Isidor Rabi in 1938, by extending the Stern–Gerlach experiment, and in 1944, Rabi was awarded the Nobel Prize in Physics for this work. In 1946, Felix Bloch and Edward Mills Purcell expanded the technique for use on liquids and solids, for which they shared the Nobel Prize in Physics in 1952.

Russell H. Varian filed the "Method and means for correlating nuclear properties of atoms and magnetic fields", U.S. Patent 2,561,490 on July 24, 1951. Varian Associates developed the first NMR unit called NMR HR-30 in 1952.

Purcell had worked on the development of radar during World War II at the Massachusetts Institute of Technology's Radiation Laboratory. His work during that project on the production and detection of radio frequency power and on the absorption of such RF power by matter laid the foundation for his discovery of NMR in bulk matter.

Rabi, Bloch, and Purcell observed that magnetic nuclei, like ¹H and ³¹P, could absorb RF energy when placed in a magnetic field and when the RF was of a frequency specific to the identity of the nuclei. When this absorption occurs, the nucleus is described as being in resonance. Different atomic nuclei within a molecule resonate at different (radio) frequencies for the same magnetic field strength. The observation of such magnetic resonance frequencies of the nuclei present in a molecule makes it possible to determine essential chemical and structural information about the molecule.

The improvements of the NMR method benefited from the development of electromagnetic technology and advanced electronics and their introduction into civilian use. Originally as research tool it was limited primarily to dynamic nuclear polarization, by the work of Anatole Abragam and Albert Overhauser, and to condensed matter physics, where it produced one of the first demonstrations of the validity of the BCS theory of superconductivity by the observation by Charles Slichter of the Hebel-Slichter effect. It soon showed ots potentials in organic chemistry, and by the 1990s improvement in the sensitivity and resolution of NMR spectroscopy resulted in its broader use in analytical chemistry, biochemistry and materials science.

In the 2020s zero- to ultralow-field nuclear magnetic resonance (ZULF NMR), a form of spectroscopy that provides abundant analytical results without the need for large magnetic fields, was developed. It is combined with a special technique that makes it possible to hyperpolarize atomic nuclei.

Theory of nuclear magnetic resonance

Nuclear spin and magnets

All nucleons, that is neutrons and protons, composing any atomic nucleus, have the intrinsic quantum property of spin, an intrinsic angular momentum analogous to the classical angular momentum of a spinning sphere. The overall spin of the nucleus is determined by the spin quantum number S. If the numbers of both the protons and neutrons in a given nuclide are even then S = 0, i.e. there is no overall spin. Then, just as electrons pair up in nondegenerate atomic orbitals, so do even numbers of protons or even numbers of neutrons (both of which are also spin-1/2 particles and hence fermions), giving zero overall spin.

However, a proton and neutron spin vector that aligns itself opposite to the external magnetic field vector will have a lower energy when their spins are parallel, not anti-parallel. This parallel spin alignment of distinguishable particles does not violate the Pauli exclusion principle. The lowering of energy for parallel spins has to do with the quark structure of these two nucleons. As a result, the spin ground state for the deuteron (the nucleus of deuterium, the ²H isotope of hydrogen), which has only a proton and a neutron, corresponds to a spin value of 1, not of zero. On the other hand, because of the Pauli exclusion principle, the tritium isotope of hydrogen must have a pair of anti-parallel spin neutrons (of total spin zero for the neutron-spin pair), plus a proton of spin 1/2. Therefore, the tritium total nuclear spin value is again 1/2, just like for the simpler, abundant hydrogen isotope, ¹H nucleus (the proton). The NMR absorption frequency for tritium is also similar to that of ¹H. In many other cases of non-radioactive nuclei, the overall spin is also non-zero. For example, the ²⁷Al nucleus has an overall spin value S = 5/2.

A non-zero spin [math]\displaystyle{ \vec{S} }[/math] is always associated with a non-zero magnetic dipole moment, [math]\displaystyle{ \vec{\mu} }[/math], via the relation [math]\displaystyle{ \vec{\mu} = \gamma \vec{S} }[/math] where γ is the gyromagnetic ratio. Classically, this corresponds to the proportionality between the angular momentum and the magnetic dipole moment of a spinning charged sphere, both of which are vectors parallel to the rotation axis whose length increases proportional to the spinning frequency. It is the magnetic moment and its interaction with magnetic fields that allows the observation of NMR signal associated with transitions between nuclear spin levels during resonant RF irradiation or caused by Larmor precession of the average magnetic moment after resonant irradiation. Nuclides with even numbers of both protons and neutrons have zero nuclear magnetic dipole moment and hence do not exhibit NMR signal. For instance, ¹⁸O is an example of a nuclide that produces no NMR signal, whereas ¹³C, ³¹P, ³⁵Cl and ³⁷Cl are nuclides that do exhibit NMR spectra. The last two nuclei have spin S > 1/2 and are therefore quadrupolar nuclei.

Electron spin resonance (ESR) is a related technique in which transitions between electronic rather than nuclear spin levels are detected. The basic principles are similar but the instrumentation, data analysis, and detailed theory are significantly different. Moreover, there is a much smaller number of molecules and materials with unpaired electron spins that exhibit ESR (or electron paramagnetic resonance (EPR)) absorption than those that have NMR absorption spectra. On the other hand, ESR has much higher signal per spin than NMR does.

Values of spin angular momentum

Nuclear spin is an intrinsic angular momentum that is quantized. This means that the magnitude of this angular momentum is quantized (i.e. S can only take on a restricted range of values), and also that the x, y, and z-components of the angular momentum are quantized, being restricted to integer or half-integer multiples of ħ. The integer or half-integer quantum number associated with the spin component along the z-axis or the applied magnetic field is known as the magnetic quantum number, m, and can take values from +S to −S, in integer steps. Hence for any given nucleus, there are a total of 2S + 1 angular momentum states.

The z-component of the angular momentum vector ([math]\displaystyle{ \vec{S} }[/math]) is therefore S_z = mħ, where ħ is the reduced Planck constant. The z-component of the magnetic moment is simply: [math]\displaystyle{ \mu_z = \gamma S_z = \gamma m\hbar. }[/math]

Spin energy in a magnetic field

Splitting of nuclei spin energies in an external magnetic field

An intuitive model. Nuclei with spin have magnetic moments (spin magnetic moments). By itself, there is no energetic difference for any particular orientation of the nuclear magnet (only one energy state, on the left), but in an external magnetic field there is a high-energy state and a low-energy state depending on the relative orientation of the magnet to the external field, and in thermal equilibrium, the low-energy orientation is preferred. The average orientation of the magnetic moment will precess around the field. The external field can be supplied by a large magnet and also by other nuclei in the vicinity.

Consider nuclei with a spin of one-half, like ¹H, ¹³C or ¹⁹F. Each nucleus has two linearly independent spin states, with m = 1/2 or m = −1/2 (also referred to as spin-up and spin-down, or sometimes α and β spin states, respectively) for the z-component of spin. In the absence of a magnetic field, these states are degenerate; that is, they have the same energy. Hence the number of nuclei in these two states will be essentially equal at thermal equilibrium.

If a nucleus is placed in a magnetic field, however, the two states no longer have the same energy as a result of the interaction between the nuclear magnetic dipole moment and the external magnetic field. The energy of a magnetic dipole moment [math]\displaystyle{ \vec{\mu} }[/math] in a magnetic field B₀ is given by: [math]\displaystyle{ E = -\vec{\mu} \cdot \mathbf{B}_0 = -\mu_x B_{0x}-\mu_y B_{0y} - \mu_z B_{0z} . }[/math]

Usually the z-axis is chosen to be along B₀, and the above expression reduces to: [math]\displaystyle{ E = -\mu_\mathrm{z} B_0 \, , }[/math] or alternatively: [math]\displaystyle{ E = -\gamma m\hbar B_0 \, . }[/math]

As a result, the different nuclear spin states have different energies in a non-zero magnetic field. In less formal language, we can talk about the two spin states of a spin 1/2 as being aligned either with or against the magnetic field. If γ is positive (true for most isotopes used in NMR) then m = 1/2 is the lower energy state.

The energy difference between the two states is: [math]\displaystyle{ \Delta{E} = \gamma \hbar B_0 \, , }[/math] and this results in a small population bias favoring the lower energy state in thermal equilibrium. With more spins pointing up than down, a net spin magnetization along the magnetic field B₀ results.

Precession of the spin magnetization

Further information: Physics:Larmor precession

A central concept in NMR is the precession of the spin magnetization around the magnetic field at the nucleus, with the angular frequency [math]\displaystyle{ \omega = -\gamma B }[/math] where [math]\displaystyle{ \omega = 2 \pi \nu }[/math] relates to the oscillation frequency [math]\displaystyle{ \nu }[/math] and B is the magnitude of the field. This means that the spin magnetization, which is proportional to the sum of the spin vectors of nuclei in magnetically equivalent sites (the expectation value of the spin vector in quantum mechanics), moves on a cone around the B field. This is analogous to the precessional motion of the axis of a tilted spinning top around the gravitational field. In quantum mechanics, [math]\displaystyle{ \omega }[/math] is the Bohr frequency [math]\displaystyle{ \Delta{E}/\hbar }[/math] of the [math]\displaystyle{ S_x }[/math] and [math]\displaystyle{ S_y }[/math] expectation values. Precession of non-equilibrium magnetization in the applied magnetic field B₀ occurs with the Larmor frequency [math]\displaystyle{ \omega_L = 2 \pi \nu_L = -\gamma B_0, }[/math] without change in the populations of the energy levels because energy is constant (time-independent Hamiltonian).

Magnetic resonance and radio-frequency pulses

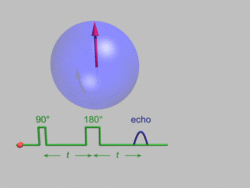
A perturbation of nuclear spin orientations from equilibrium will occur only when an oscillating magnetic field is applied whose frequency ν_rf sufficiently closely matches the Larmor precession frequency ν_L of the nuclear magnetization. The populations of the spin-up and -down energy levels then undergo Rabi oscillations, which are analyzed most easily in terms of precession of the spin magnetization around the effective magnetic field in a reference frame rotating with the frequency ν_rf. The stronger the oscillating field, the faster the Rabi oscillations or the precession around the effective field in the rotating frame. After a certain time on the order of 2–1000 microseconds, a resonant RF pulse flips the spin magnetization to the transverse plane, i.e. it makes an angle of 90° with the constant magnetic field B₀ ("90° pulse"), while after a twice longer time, the initial magnetization has been inverted ("180° pulse"). It is the transverse magnetization generated by a resonant oscillating field which is usually detected in NMR, during application of the relatively weak RF field in old-fashioned continuous-wave NMR, or after the relatively strong RF pulse in modern pulsed NMR.

Chemical shielding

It might appear from the above that all nuclei of the same nuclide (and hence the same γ) would resonate at exactly the same frequency. This is not the case. The most important perturbation of the NMR frequency for applications of NMR is the "shielding" effect of the surrounding shells of electrons. Electrons, similar to the nucleus, are also charged and rotate with a spin to produce a magnetic field opposite to the applied magnetic field. In general, this electronic shielding reduces the magnetic field at the nucleus (which is what determines the NMR frequency). As a result, the frequency required to achieve resonance is also reduced. This shift in the NMR frequency due to the electronic molecular orbital coupling to the external magnetic field is called chemical shift, and it explains why NMR is able to probe the chemical structure of molecules, which depends on the electron density distribution in the corresponding molecular orbitals. If a nucleus in a specific chemical group is shielded to a higher degree by a higher electron density of its surrounding molecular orbital, then its NMR frequency will be shifted "upfield" (that is, a lower chemical shift), whereas if it is less shielded by such surrounding electron density, then its NMR frequency will be shifted "downfield" (that is, a higher chemical shift).

Unless the local symmetry of such molecular orbitals is very high (leading to "isotropic" shift), the shielding effect will depend on the orientation of the molecule with respect to the external field (B₀). In solid-state NMR spectroscopy, magic angle spinning is required to average out this orientation dependence in order to obtain frequency values at the average or isotropic chemical shifts. This is unnecessary in conventional NMR investigations of molecules in solution, since rapid "molecular tumbling" averages out the chemical shift anisotropy (CSA). In this case, the "average" chemical shift (ACS) or isotropic chemical shift is often simply referred to as the chemical shift.

Relaxation

Further information: Physics:Relaxation (NMR)

File:Proton spin MRI.webm

The process of population relaxation refers to nuclear spins that return to thermodynamic equilibrium in the magnet. This process is also called T₁, "spin-lattice" or "longitudinal magnetic" relaxation, where T₁ refers to the mean time for an individual nucleus to return to its thermal equilibrium state of the spins. After the nuclear spin population has relaxed, it can be probed again, since it is in the initial, equilibrium (mixed) state.

The precessing nuclei can also fall out of alignment with each other and gradually stop producing a signal. This is called T₂ or transverse relaxation. Because of the difference in the actual relaxation mechanisms involved (for example, intermolecular versus intramolecular magnetic dipole-dipole interactions ), T₁ is usually (except in rare cases) longer than T₂ (that is, slower spin-lattice relaxation, for example because of smaller dipole-dipole interaction effects). In practice, the value of T₂* which is the actually observed decay time of the observed NMR signal, or free induction decay (to 1/e of the initial amplitude immediately after the resonant RF pulse), also depends on the static magnetic field inhomogeneity, which is quite significant. (There is also a smaller but significant contribution to the observed FID shortening from the RF inhomogeneity of the resonant pulse). In the corresponding FT-NMR spectrum—meaning the Fourier transform of the free induction decay—the T₂* time is inversely related to the width of the NMR signal in frequency units. Thus, a nucleus with a long T₂ relaxation time gives rise to a very sharp NMR peak in the FT-NMR spectrum for a very homogeneous ("well-shimmed") static magnetic field, whereas nuclei with shorter T₂ values give rise to broad FT-NMR peaks even when the magnet is shimmed well. Both T₁ and T₂ depend on the rate of molecular motions as well as the gyromagnetic ratios of both the resonating and their strongly interacting, next-neighbor nuclei that are not at resonance.

A Hahn echo decay experiment measuring dephasing time.

A Hahn echo decay experiment can be used to measure the dephasing time, as shown in the animation. The size of the echo is recorded for different spacings of the two pulses. This reveals the decoherence that is not refocused by the 180° pulse. In simple cases, an exponential decay is measured which is described by the T₂ time.

NMR spectroscopy

900 MHz, 21.2 T NMR Magnet at HWB-NMR, Birmingham, UK

NMR spectroscopy is one of the principal techniques used to obtain physical, chemical, electronic and structural information about molecules due to the chemical shift of the resonance frequencies of the nuclear spins in the sample. Peak splittings due to J- or dipolar couplings between nuclei are also useful. NMR spectroscopy can provide detailed and quantitative information on the functional groups, topology, dynamics and three-dimensional structure of molecules in solution and the solid state. Since the area under an NMR peak is usually proportional to the number of spins involved, peak integrals can be used to determine composition quantitatively.

Structure and molecular dynamics can be studied (with or without "magic angle" spinning (MAS)) by NMR of quadrupolar nuclei (that is, with spin S > 1/2) even in the presence of magnetic "dipole-dipole" interaction broadening (or simply, dipolar broadening), which is always much smaller than the quadrupolar interaction strength because it is a magnetic vs. an electric interaction effect.

Additional structural and chemical information may be obtained by performing double-quantum NMR experiments for pairs of spins or quadrupolar nuclei such as ²H. Furthermore, nuclear magnetic resonance is one of the techniques that has been used to design quantum automata, and also build elementary quantum computers.

Continuous-wave (CW) spectroscopy

In the first few decades of nuclear magnetic resonance, spectrometers used a technique known as continuous-wave (CW) spectroscopy, where the transverse spin magnetization generated by a weak oscillating magnetic field is recorded as a function of the oscillation frequency or static field strength B₀. When the oscillation frequency matches the nuclear resonance frequency, the transverse magnetization is maximized and a peak is observed in the spectrum. Although NMR spectra could be, and have been, obtained using a fixed constant magnetic field and sweeping the frequency of the oscillating magnetic field, it was more convenient to use a fixed frequency source and vary the current (and hence magnetic field) in an electromagnet to observe the resonant absorption signals. This is the origin of the counterintuitive, but still common, "high field" and "low field" terminology for low frequency and high frequency regions, respectively, of the NMR spectrum.

As of 1996, CW instruments were still used for routine work because the older instruments were cheaper to maintain and operate, often operating at 60 MHz with correspondingly weaker (non-superconducting) electromagnets cooled with water rather than liquid helium. One radio coil operated continuously, sweeping through a range of frequencies, while another orthogonal coil, designed not to receive radiation from the transmitter, received signals from nuclei that reoriented in solution. As of 2014, low-end refurbished 60 MHz and 90 MHz systems were sold as FT-NMR instruments, and in 2010 the "average workhorse" NMR instrument was configured for 300 MHz.

CW spectroscopy is inefficient in comparison with Fourier analysis techniques (see below) since it probes the NMR response at individual frequencies or field strengths in succession. Since the NMR signal is intrinsically weak, the observed spectrum suffers from a poor signal-to-noise ratio. This can be mitigated by signal averaging, i.e. adding the spectra from repeated measurements. While the NMR signal is the same in each scan and so adds linearly, the random noise adds more slowly – proportional to the square root of the number of spectra (see random walk). Hence the overall signal-to-noise ratio increases as the square-root of the number of spectra measured. However, monitoring an NMR signal at a single frequency as a function of time may be better suited for kinetic studies than pulsed Fourier-transform NMR spectrosocopy.

Fourier-transform spectroscopy

Most applications of NMR involve full NMR spectra, that is, the intensity of the NMR signal as a function of frequency. Early attempts to acquire the NMR spectrum more efficiently than simple CW methods involved illuminating the target simultaneously with more than one frequency. A revolution in NMR occurred when short radio-frequency pulses began to be used, with a frequency centered at the middle of the NMR spectrum. In simple terms, a short pulse of a given "carrier" frequency "contains" a range of frequencies centered about the carrier frequency, with the range of excitation (bandwidth) being inversely proportional to the pulse duration, i.e. the Fourier transform of a short pulse contains contributions from all the frequencies in the neighborhood of the principal frequency. The restricted range of the NMR frequencies made it relatively easy to use short (1 - 100 microsecond) radio frequency pulses to excite the entire NMR spectrum.

Applying such a pulse to a set of nuclear spins simultaneously excites all the single-quantum NMR transitions. In terms of the net magnetization vector, this corresponds to tilting the magnetization vector away from its equilibrium position (aligned along the external magnetic field). The out-of-equilibrium magnetization vector then precesses about the external magnetic field vector at the NMR frequency of the spins. This oscillating magnetization vector induces a voltage in a nearby pickup coil, creating an electrical signal oscillating at the NMR frequency. This signal is known as the free induction decay (FID), and it contains the sum of the NMR responses from all the excited spins. In order to obtain the frequency-domain NMR spectrum (NMR absorption intensity vs. NMR frequency) this time-domain signal (intensity vs. time) must be Fourier transformed. Fortunately, the development of Fourier transform (FT) NMR coincided with the development of digital computers and the digital fast Fourier transform (FFT). Fourier methods can be applied to many types of spectroscopy. Richard R. Ernst was one of the pioneers of pulsed NMR and won a Nobel Prize in chemistry in 1991 for his work on Fourier Transform NMR and his development of multi-dimensional NMR spectroscopy.

Multi-dimensional NMR spectroscopy

The use of pulses of different durations, frequencies, or shapes in specifically designed patterns or pulse sequences allows production of a spectrum that contains many different types of information about the molecules in the sample. In multi-dimensional nuclear magnetic resonance spectroscopy, there are at least two pulses: one leads to the directly detected signal and the others affect the starting magnetization and spin state prior to it. The full analysis involves repeating the sequence with the pulse timings systematically varied in order to probe the oscillations of the spin system are point by point in the time domain. Multidimensional Fourier transformation of the multidimensional time signal yields the multidimensional spectrum. In two-dimensional nuclear magnetic resonance spectroscopy (2D-NMR), there will be one systematically varied time period in the sequence of pulses, which will modulate the intensity or phase of the detected signals. In 3D-NMR, two time periods will be varied independently, and in 4D-NMR, three will be varied.

There are many such experiments. In some, fixed time intervals allow (among other things) magnetization transfer between nuclei and, therefore, the detection of the kinds of nuclear–nuclear interactions that allowed for the magnetization transfer. Interactions that can be detected are usually classified into two kinds. There are through-bond and through-space interactions. Through-bond interactions relate to structural connectivity of the atoms and provide information about which ones are directly connected to each other, connected by way of a single other intermediate atom, etc. Through-space interactions relate to actual geometric distances and angles, including effects of dipolar coupling and the nuclear Overhauser effect.

Although the fundamental concept of 2D-FT NMR was proposed by Jean Jeener from the Free University of Brussels at an international conference, this idea was largely developed by Richard Ernst, who won the 1991 Nobel prize in Chemistry for his work in FT NMR, including multi-dimensional FT NMR, and especially 2D-FT NMR of small molecules. Multi-dimensional FT NMR experiments were then further developed into powerful methodologies for studying molecules in solution, in particular for the determination of the structure of biopolymers such as proteins or even small nucleic acids.

In 2002 Kurt Wüthrich shared the Nobel Prize in Chemistry (with John Bennett Fenn and Koichi Tanaka) for his work with protein FT NMR in solution.

Solid-state NMR spectroscopy

This technique complements X-ray crystallography in that it is frequently applicable to molecules in an amorphous or liquid-crystalline state, whereas crystallography, as the name implies, is performed on molecules in a crystalline phase. In electronically conductive materials, the Knight shift of the resonance frequency can provide information on the mobile charge carriers. Though nuclear magnetic resonance is used to study the structure of solids, extensive atomic-level structural detail is more challenging to obtain in the solid state. Due to broadening by chemical shift anisotropy (CSA) and dipolar couplings to other nuclear spins, without special techniques such as MAS or dipolar decoupling by RF pulses, the observed spectrum is often only a broad Gaussian band for non-quadrupolar spins in a solid.

Professor Raymond Andrew at the University of Nottingham in the UK pioneered the development of high-resolution solid-state nuclear magnetic resonance. He was the first to report the introduction of the MAS (magic angle sample spinning; MASS) technique that allowed him to achieve spectral resolution in solids sufficient to distinguish between chemical groups with either different chemical shifts or distinct Knight shifts. In MASS, the sample is spun at several kilohertz around an axis that makes the so-called magic angle θ_m (which is ~54.74°, where 3cos²θ_m-1 = 0) with respect to the direction of the static magnetic field B₀; as a result of such magic angle sample spinning, the broad chemical shift anisotropy bands are averaged to their corresponding average (isotropic) chemical shift values. Correct alignment of the sample rotation axis as close as possible to θ_m is essential for cancelling out the chemical-shift anisotropy broadening. There are different angles for the sample spinning relative to the applied field for the averaging of electric quadrupole interactions and paramagnetic interactions, correspondingly ~30.6° and ~70.1°. In amorphous materials, residual line broadening remains since each segment is in a slightly different environment, therefore exhibiting a slightly different NMR frequency.

Dipolar and J-couplings to nearby ¹H nuclei are usually removed by radio-frequency pulses applied at the ¹H frequency during signal detection. The concept of cross polarization developed by Sven Hartmann and Erwin Hahn was utilized in transferring magnetization from protons to less sensitive nuclei by M.G. Gibby, Alex Pines and John S. Waugh. Then, Jake Schaefer and Ed Stejskal demonstrated the powerful use of cross polarization under MAS conditions (CP-MAS) and proton decoupling, which is now routinely employed to measure high resolution spectra of low-abundance and low-sensitivity nuclei, such as carbon-13, silicon-29, or nitrogen-15, in solids. Significant further signal enhancement can be achieved by dynamic nuclear polarization from unpaired electrons to the nuclei, usually at temperatures near 110 K.

Sensitivity

Because the intensity of nuclear magnetic resonance signals and, hence, the sensitivity of the technique depends on the strength of the magnetic field, the technique has also advanced over the decades with the development of more powerful magnets. Advances made in audio-visual technology have also improved the signal-generation and processing capabilities of newer instruments.

As noted above, the sensitivity of nuclear magnetic resonance signals is also dependent on the presence of a magnetically susceptible nuclide and, therefore, either on the natural abundance of such nuclides or on the ability of the experimentalist to artificially enrich the molecules, under study, with such nuclides. The most abundant naturally occurring isotopes of hydrogen and phosphorus (for example) are both magnetically susceptible and readily useful for nuclear magnetic resonance spectroscopy. In contrast, carbon and nitrogen have useful isotopes but which occur only in very low natural abundance.

Other limitations on sensitivity arise from the quantum-mechanical nature of the phenomenon. For quantum states separated by energy equivalent to radio frequencies, thermal energy from the environment causes the populations of the states to be close to equal. Since incoming radiation is equally likely to cause stimulated emission (a transition from the upper to the lower state) as absorption, the NMR effect depends on an excess of nuclei in the lower states. Several factors can reduce sensitivity, including:

• Increasing temperature, which evens out the population of states. Conversely, low temperature NMR can sometimes yield better results than room-temperature NMR, providing the sample remains liquid.
• Saturation of the sample with energy applied at the resonant radiofrequency. This manifests in both CW and pulsed NMR; in the first case (CW) this happens by using too much continuous power that keeps the upper spin levels completely populated; in the second case (pulsed), each pulse (that is at least a 90° pulse) leaves the sample saturated, and four to five times the (longitudinal) relaxation time (5T₁) must pass before the next pulse or pulse sequence can be applied. For single pulse experiments, shorter RF pulses that tip the magnetization by less than 90° can be used, which loses some intensity of the signal, but allows for shorter recycle delays. The optimum there is called an Ernst angle, after the Nobel laureate. Especially in solid state NMR, or in samples containing very few nuclei with spin (diamond with the natural 1% of carbon-13 is especially troublesome here) the longitudinal relaxation times can be on the range of hours, while for proton-NMR they are more in the range of one second.
• Non-magnetic effects, such as electric-quadrupole coupling of spin-1 and spin-3/2 nuclei with their local environment, which broaden and weaken absorption peaks. ¹⁴N, an abundant spin-1 nucleus, is difficult to study for this reason. High resolution NMR instead probes molecules using the rarer ¹⁵N isotope, which has spin-1/2.

Isotopes

Many isotopes of chemical elements can be used for NMR analysis.

Commonly used nuclei:

• ¹H, the most commonly used spin-1/2 nucleus in NMR investigation, has been studied using many forms of NMR. Hydrogen is highly abundant, especially in biological systems. It is the nucleus most sensitive to NMR signal (apart from ³H, which is not commonly used due to its instability and radioactivity). Proton NMR produces narrow chemical shift with sharp signals. Fast acquisition of quantitative results (peak integrals in stoichiometric ratio) is possible due to short relaxation time. The ¹H signal has been the sole diagnostic nucleus used for clinical magnetic resonance imaging (MRI).
• ²H, a spin-1 nucleus commonly utilized as signal-free medium in the form of deuterated solvents during proton NMR, to avoid signal interference from hydrogen-containing solvents in measurement of ¹H solutes. Also used in determining the behavior of lipids in lipid membranes and other solids or liquid crystals as it is a relatively non-perturbing label which can selectively replace ¹H. Alternatively, ²H can be detected in media specially labeled with ²H. Deuterium resonance is commonly used in high-resolution NMR spectroscopy to monitor drifts in the magnetic field strength (lock) and to monitor the homogeneity of the external magnetic field.
• ³He, is very sensitive to NMR. There is a very low percentage in natural helium, and subsequently has to be purified from ⁴He. It is used mainly in studies of endohedral fullerenes, where its chemical inertness is beneficial to ascertaining the structure of the entrapping fullerene.
• ¹¹B, more sensitive than ¹⁰B, yields sharper signals. The nuclear spin of ¹⁰B is 3 and that of ¹¹B is 3/2. Quartz tubes must be used because borosilicate glass interferes with measurement.
• ¹³C spin-1/2, is widely used, despite its relative paucity in naturally occurring carbon (approximately 1.1%). It is stable to nuclear decay. Since there is a low percentage in natural carbon, spectrum acquisition on samples which have not been experimentally enriched in ¹³C takes a long time. Frequently used for labeling of compounds in synthetic and metabolic studies. Has low sensitivity and moderately wide chemical shift range, yields sharp signals. Low percentage makes it useful by preventing spin-spin couplings and makes the spectrum appear less crowded. Slow relaxation means that spectra are not integrable unless long acquisition times are used.
• ¹⁴N, spin-1, medium sensitivity nucleus with wide chemical shift range. Its large quadrupole moment interferes in acquisition of high resolution spectra, limiting usefulness to smaller molecules and functional groups with a high degree of symmetry such as the headgroups of lipids.
• ¹⁵N, spin-1/2, relatively commonly used. Can be used for isotopically labeling compounds. Very insensitive but yields sharp signals. Low percentage in natural nitrogen together with low sensitivity requires high concentrations or expensive isotope enrichment.
• ¹⁷O, spin-5/2, low sensitivity and very low natural abundance (0.037%), wide chemical shift range (up to 2000 ppm). Quadrupole moment causing line broadening. Used in metabolic and biochemical studies in studies of chemical equilibria.
• ¹⁹F, spin-1/2, relatively commonly measured. Sensitive, yields sharp signals, has a wide chemical shift range.
• ³¹P, spin-1/2, 100% of natural phosphorus. Medium sensitivity, wide chemical shift range, yields sharp lines. Spectra tend to have a moderate amount of noise. Used in biochemical studies and in coordination chemistry with phosphorus-containing ligands.
• ³⁵Cl and ³⁷Cl, spin-3/2, broad signal. ³⁵Cl is significantly more sensitive, preferred over ³⁷Cl despite its slightly broader signal. Organic chlorides yield very broad signals. Its use is limited to inorganic and ionic chlorides and very small organic molecules.
• ⁴³Ca, spin-7/2, relatively small quadrupole moment, moderately sensitive, very low natural abundance. Used in biochemistry to study calcium binding to DNA, proteins, etc.
• ¹⁹⁵Pt, used in studies of catalysts and complexes.

Other nuclei (usually used in the studies of their complexes and chemical bonding, or to detect presence of the element):

• ⁶Li, ⁷Li
• ⁹Be
• ¹⁹F
• ²¹Ne
• ²³Na
• ²⁵Mg
• ²⁷Al
• ²⁹Si
• ³¹P
• ³³S
• ³⁹K, ⁴⁰K, ⁴¹K
• ⁴⁵Sc
• ⁴⁷Ti, ⁴⁹Ti
• ⁵⁰V, ⁵¹V
• ⁵³Cr
• ⁵⁵Mn
• ⁵⁷Fe
• ⁵⁹Co
• ⁶¹Ni
• ⁶³Cu, ⁶⁵Cu
• ⁶⁷Zn
• ⁶⁹Ga, ⁷¹Ga
• ⁷³Ge
• ⁷⁵As
• ⁷⁷Se
• ⁸¹Br
• ⁸⁷Rb
• ⁸⁷Sr
• ⁹⁵Mo
• ¹⁰⁹Ag
• ¹¹³Cd
• ¹¹⁹Sn
• ¹²⁵Te
• ¹²⁷I
• ¹³³Cs
• ¹³⁵Ba, ¹³⁷Ba
• ¹³⁹La
• ¹⁸³W
• ¹⁹⁹Hg

Applications

NMR is extensively used in medicine in the form of magnetic resonance imaging. NMR is used in organic chemistry and industrially mainly for analysis of chemicals. The technique is also used to measure the ratio between water and fat in foods, monitor the flow of corrosive fluids in pipes, or to study molecular structures such as catalysts.

Medicine

Medical MRI

The application of nuclear magnetic resonance best known to the general public is magnetic resonance imaging for medical diagnosis and magnetic resonance microscopy in research settings. However, it is also widely used in biochemical studies, notably in NMR spectroscopy such as proton NMR, carbon-13 NMR, deuterium NMR and phosphorus-31 NMR. Biochemical information can also be obtained from living tissue (e.g. human brain tumors) with the technique known as in vivo magnetic resonance spectroscopy or chemical shift NMR microscopy.

These spectroscopic studies are possible because nuclei are surrounded by orbiting electrons, which are charged particles that generate small, local magnetic fields that add to or subtract from the external magnetic field, and so will partially shield the nuclei. The amount of shielding depends on the exact local environment. For example, a hydrogen bonded to an oxygen will be shielded differently from a hydrogen bonded to a carbon atom. In addition, two hydrogen nuclei can interact via a process known as spin-spin coupling, if they are on the same molecule, which will split the lines of the spectra in a recognizable way.

As one of the two major spectroscopic techniques used in metabolomics, NMR is used to generate metabolic fingerprints from biological fluids to obtain information about disease states or toxic insults.

Chemistry

By studying the peaks of nuclear magnetic resonance spectra, chemists can determine the structure of many compounds. It can be a very selective technique, distinguishing among many atoms within a molecule or collection of molecules of the same type but which differ only in terms of their local chemical environment. NMR spectroscopy is used to unambiguously identify known and novel compounds, and as such, is usually required by scientific journals for identity confirmation of synthesized new compounds. See the articles on carbon-13 NMR and proton NMR for detailed discussions.

A chemist can determine the identity of a compound by comparing the observed nuclear precession frequencies to known frequencies. Further structural data can be elucidated by observing spin-spin coupling, a process by which the precession frequency of a nucleus can be influenced by the spin orientation of a chemically bonded nucleus. Spin-spin coupling is easily observed in NMR of hydrogen-1 (¹H NMR) since its natural abundance is nearly 100%.

Because the nuclear magnetic resonance timescale is rather slow, compared to other spectroscopic methods, changing the temperature of a T₂* experiment can also give information about fast reactions, such as the Cope rearrangement or about structural dynamics, such as ring-flipping in cyclohexane. At low enough temperatures, a distinction can be made between the axial and equatorial hydrogens in cyclohexane.

An example of nuclear magnetic resonance being used in the determination of a structure is that of buckminsterfullerene (often called "buckyballs", composition C₆₀). This now famous form of carbon has 60 carbon atoms forming a sphere. The carbon atoms are all in identical environments and so should see the same internal H field. Unfortunately, buckminsterfullerene contains no hydrogen and so ¹³C nuclear magnetic resonance has to be used. ¹³C spectra require longer acquisition times since carbon-13 is not the common isotope of carbon (unlike hydrogen, where ¹H is the common isotope). However, in 1990 the spectrum was obtained by R. Taylor and co-workers at the University of Sussex and was found to contain a single peak, confirming the unusual structure of buckminsterfullerene.

Purity determination (w/w NMR)

While NMR is primarily used for structural determination, it can also be used for purity determination, provided that the structure and molecular weight of the compound is known. This technique requires the use of an internal standard of known purity. Typically this standard will have a high molecular weight to facilitate accurate weighing, but relatively few protons so as to give a clear peak for later integration e.g. 1,2,4,5-tetrachloro-3-nitrobenzene. Accurately weighed portions of the standard and sample are combined and analysed by NMR. Suitable peaks from both compounds are selected and the purity of the sample is determined via the following equation.

[math]\displaystyle{ \mathrm{Purity} = \frac{w_\mathrm{std} \times n[\mathrm{H}]_\mathrm{std} \times MW_\mathrm{spl}}{w_\mathrm{spl} \times MW_\mathrm{std} \times n[\mathrm{H}]_\mathrm{spl}} \times P }[/math]

Where:

• w_std: weight of internal standard
• w_spl: weight of sample
• n[H]_std: the integrated area of the peak selected for comparison in the standard, corrected for the number of protons in that functional group
• n[H]_spl: the integrated area of the peak selected for comparison in the sample, corrected for the number of protons in that functional group
• MW_std: molecular weight of standard
• MW_spl: molecular weight of sample
• P: purity of internal standard

Non-destructive testing

Nuclear magnetic resonance is extremely useful for analyzing samples non-destructively. Radio-frequency magnetic fields easily penetrate many types of matter and anything that is not highly conductive or inherently ferromagnetic. For example, various expensive biological samples, such as nucleic acids, including RNA and DNA, or proteins, can be studied using nuclear magnetic resonance for weeks or months before using destructive biochemical experiments. This also makes nuclear magnetic resonance a good choice for analyzing dangerous samples.

Segmental and molecular motions

In addition to providing static information on molecules by determining their 3D structures, one of the remarkable advantages of NMR over X-ray crystallography is that it can be used to obtain important dynamic information. This is due to the orientation dependence of the chemical-shift, dipole-coupling, or electric-quadrupole-coupling contributions to the instantaneous NMR frequency in an anisotropic molecular environment. When the molecule or segment containing the NMR-observed nucleus changes its orientation relative to the external field, the NMR frequency changes, which can result in changes in one- or two-dimensional spectra or in the relaxation times, depending on the correlation time and amplitude of the motion.

Data acquisition in the petroleum industry

Another use for nuclear magnetic resonance is data acquisition in the petroleum industry for petroleum and natural gas exploration and recovery. Initial research in this domain began in the 1950s, however, the first commercial instruments were not released until the early 1990s. A borehole is drilled into rock and sedimentary strata into which nuclear magnetic resonance logging equipment is lowered. Nuclear magnetic resonance analysis of these boreholes is used to measure rock porosity, estimate permeability from pore size distribution and identify pore fluids (water, oil and gas). These instruments are typically low field NMR spectrometers.

NMR logging, a subcategory of electromagnetic logging, measures the induced magnet moment of hydrogen nuclei (protons) contained within the fluid-filled pore space of porous media (reservoir rocks). Unlike conventional logging measurements (e.g., acoustic, density, neutron, and resistivity), which respond to both the rock matrix and fluid properties and are strongly dependent on mineralogy, NMR-logging measurements respond to the presence of hydrogen. Because hydrogen atoms primarily occur in pore fluids, NMR effectively responds to the volume, composition, viscosity, and distribution of these fluids, for example oil, gas or water. NMR logs provide information about the quantities of fluids present, the properties of these fluids, and the sizes of the pores containing these fluids. From this information, it is possible to infer or estimate:

• The volume (porosity) and distribution (permeability) of the rock pore space
• Rock composition
• Type and quantity of fluid hydrocarbons
• Hydrocarbon producibility

The basic core and log measurement is the T₂ decay, presented as a distribution of T₂ amplitudes versus time at each sample depth, typically from 0.3 ms to 3 s. The T₂ decay is further processed to give the total pore volume (the total porosity) and pore volumes within different ranges of T₂. The most common volumes are the bound fluid and free fluid. A permeability estimate is made using a transform such as the Timur-Coates or SDR permeability transforms. By running the log with different acquisition parameters, direct hydrocarbon typing and enhanced diffusion are possible.

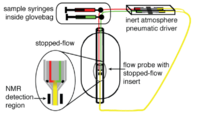
Flow probes for NMR spectroscopy

Schematic diagram of a NMR Stopped Flow Probe

Recently, real-time applications of NMR in liquid media have been developed using specifically designed flow probes (flow cell assemblies) which can replace standard tube probes. This has enabled techniques that can incorporate the use of high performance liquid chromatography (HPLC) or other continuous flow sample introduction devices. These flow probes have used in various online process monitoring such as chemical reactions and environmental pollutant degradation.

Process control

NMR has now entered the arena of real-time process control and process optimization in oil refineries and petrochemical plants. Two different types of NMR analysis are utilized to provide real time analysis of feeds and products in order to control and optimize unit operations. Time-domain NMR (TD-NMR) spectrometers operating at low field (2–20 MHz for ¹H) yield free induction decay data that can be used to determine absolute hydrogen content values, rheological information, and component composition. These spectrometers are used in mining, polymer production, cosmetics and food manufacturing as well as coal analysis. High resolution FT-NMR spectrometers operating in the 60 MHz range with shielded permanent magnet systems yield high resolution ¹H NMR spectra of refinery and petrochemical streams. The variation observed in these spectra with changing physical and chemical properties is modeled using chemometrics to yield predictions on unknown samples. The prediction results are provided to control systems via analogue or digital outputs from the spectrometer.

Earth's field NMR

In the Earth's magnetic field, NMR frequencies are in the audio frequency range, or the very low frequency and ultra low frequency bands of the radio frequency spectrum. Earth's field NMR (EFNMR) is typically stimulated by applying a relatively strong dc magnetic field pulse to the sample and, after the end of the pulse, analyzing the resulting low frequency alternating magnetic field that occurs in the Earth's magnetic field due to free induction decay (FID). These effects are exploited in some types of magnetometers, EFNMR spectrometers, and MRI imagers. Their inexpensive portable nature makes these instruments valuable for field use and for teaching the principles of NMR and MRI.

An important feature of EFNMR spectrometry compared with high-field NMR is that some aspects of molecular structure can be observed more clearly at low fields and low frequencies, whereas other aspects observable at high fields are not observable at low fields. This is because:

• Electron-mediated heteronuclear J-couplings (spin-spin couplings) are field independent, producing clusters of two or more frequencies separated by several Hz, which are more easily observed in a fundamental resonance of about 2 kHz."Indeed it appears that enhanced resolution is possible due to the long spin relaxation times and high field homogeneity which prevail in EFNMR."
• Chemical shifts of several ppm are clearly separated in high field NMR spectra, but have separations of only a few millihertz at proton EFNMR frequencies, so are usually not resolved.

Zero field NMR

In zero field NMR all magnetic fields are shielded such that magnetic fields below 1 nT (nanotesla) are achieved and the nuclear precession frequencies of all nuclei are close to zero and indistinguishable. Under those circumstances the observed spectra are no-longer dictated by chemical shifts but primarily by J-coupling interactions which are independent of the external magnetic field. Since inductive detection schemes are not sensitive at very low frequencies, on the order of the J-couplings (typically between 0 and 1000 Hz), alternative detection schemes are used. Specifically, sensitive magnetometers turn out to be good detectors for zero field NMR. A zero magnetic field environment does not provide any polarization hence it is the combination of zero field NMR with hyperpolarization schemes that makes zero field NMR desirable.

Quantum computing

NMR quantum computing uses the spin states of nuclei within molecules as qubits. NMR differs from other implementations of quantum computers in that it uses an ensemble of systems; in this case, molecules.

Magnetometers

Various magnetometers use NMR effects to measure magnetic fields, including proton precession magnetometers (PPM) (also known as proton magnetometers), and Overhauser magnetometers.

SNMR

Surface magnetic resonance (or magnetic resonance sounding) is based on the principle of nuclear magnetic resonance (NMR) and measurements can be used to indirectly estimate the water content of saturated and unsaturated zones in the earth's subsurface. SNMR is used to estimate aquifer properties, including quantity of water contained in the aquifer, porosity, and hydraulic conductivity.

Makers of NMR equipment

Major NMR instrument makers include Thermo Fisher Scientific, Magritek, Oxford Instruments, Bruker, Spinlock SRL, General Electric, JEOL, Kimble Chase, Philips, Siemens AG, and formerly Agilent Technologies (who acquired Varian, Inc.).

See also

• Benchtop NMR spectrometer
• Larmor equation (Not to be confused with Larmor formula).
• Least-squares spectral analysis
• Liquid nitrogen
• NMR crystallography
• NMR spectra database
• Nuclear magnetic resonance in porous media
• Nuclear quadrupole resonance (NQR)
• Protein dynamics
• Rabi cycle
• Relaxometry
• Spin echo
• Structure-based assignment

Further reading

• A. Abragam (1961). The Principles of Nuclear Magnetism. Clarendon Press. ISBN 9780198520146. 
• J.W. Akitt; B.E. Mann (2000). NMR and Chemistry. Cheltenham, UK: Stanley Thornes. pp. 273, 287. ISBN 978-0-7487-4344-5. 
• K.V.R. Chary, Girjesh Govil (2008) NMR in Biological Systems: From Molecules to Human. Springer. ISBN:978-1-4020-6680-1.
• G.M. Clore; A.M. Gronenborn (1991). "Structures of larger proteins in solution: three- and four-dimensional heteronuclear NMR spectroscopy". Science 252 (5011): 1390–1399. doi:10.1126/science.2047852. PMID 2047852. Bibcode: 1991Sci...252.1390M. https://www.osti.gov/biblio/83376. 
• John Emsley; James Feeney; Leslie Howard Sutcliffe (1965). High Resolution Nuclear Magnetic Resonance Spectroscopy. Pergamon. ISBN 9781483184081. https://archive.org/details/highresolutionnu0001emsl. 
• The Feynman Lectures on Physics Vol. II Ch. 35: Paramagnetism and Magnetic Resonance
• David M. Grant; Robin Kingsley Harris (2002). "Advances in NMR". Encyclopedia of Nuclear Magnetic Resonance. John Wiley. ISBN 9780471490821. 
• R.L. Haner; P.A. Keifer (2009). "Flow Probes for NMR Spectroscopy". Encyclopedia of Magnetic Resonance. John Wiley. doi:10.1002/9780470034590.emrstm1085. ISBN 978-0470034590. 
• J.P. Hornak. "The Basics of NMR". http://www.cis.rit.edu/htbooks/nmr/. 
• J. Keeler (2005). Understanding NMR Spectroscopy. John Wiley & Sons. ISBN 978-0-470-01786-9. 
• Two-Dimensional NMR Methods for Establishing Molecular Connectivity. New York: Wiley-VCH. 1988. p. 59. ISBN 978-0-471-18707-3. https://books.google.com/books?id=9ysYrpe_NoEC. 
• J.A.Pople; W.G.Schneider; H.J.Bernstein (1959). High-resolution Nuclear Magnetic Resonance. McGraw-Hill Book Company. 
• John D. Roberts (1959). Nuclear Magnetic Resonance : applications to organic chemistry. McGraw-Hill Book Company. ISBN 9781258811662. http://resolver.caltech.edu/CaltechBOOK:1959.001. 
• Charles P. Slichter (1963). Principles of magnetic resonance: with examples from solid state physics. Harper & Row. ISBN 9783540084761. https://archive.org/details/principlesofmagn0000slic. 
• J.M. Tyszka; S.E. Fraser; R.E. Jacobs (2005). "Magnetic resonance microscopy: recent advances and applications". Current Opinion in Biotechnology 16 (1): 93–99. doi:10.1016/j.copbio.2004.11.004. PMID 15722021. 
• NMR of Proteins and Nucleic Acids. New York (NY), US: Wiley-Interscience. 1986. ISBN 978-0-471-11917-3. https://archive.org/details/nmrofproteinsnuc0000wuth. 

External links

Tutorial

• NMR/MRI tutorial
• NMR Library NMR Concepts
• NMR Course Notes
• Downloadable NMR exercises as PowerPoint (english/german) and PDF (german only) files

Animations and simulations

• A free interactive simulation of NMR principles
• Interactive simulation on the Bloch sphere

Video

• introduction to NMR and MRI
• Richard Ernst, NL – Developer of multidimensional NMR techniques Freeview video provided by the Vega Science Trust.
• 'An Interview with Kurt Wuthrich' Freeview video by the Vega Science Trust (Wüthrich was awarded a Nobel Prize in Chemistry in 2002 "for his development of nuclear magnetic resonance spectroscopy for determining the three-dimensional structure of biological macromolecules in solution").

Other

• Qian, C.; Pines, A.; Martin, R. W. (September 2007). "Off Magic Angle Spinning". Journal of Magnetic Resonance 188 (1): 183–189. doi:10.1016/j.jmr.2007.06.006. PMID 17638585. Bibcode: 2007JMagR.188..183Q. 
• Spotlight on nuclear magnetic resonance: a timeless technique