Apeirogon
| The regular apeirogon | |
|---|---|
| Edges and vertices | ∞ |
| Schläfli symbol | {∞} |
| Coxeter diagram | |
| Internal angle (degrees) | 180° |
| Dual polygon | Self-dual |
In geometry, an apeirogon (from grc ἄπειρος apeiros 'infinite, boundless', and γωνία gonia 'angle') or infinite polygon is a polygon with an infinite number of sides. Apeirogons are the two-dimensional case of infinite polytopes. In some literature, the term "apeirogon" may refer only to the regular apeirogon, with an infinite dihedral group of symmetries.[1]
Definitions
Classical constructive definition
Given a point A0 in a Euclidean space and a translation S, define the point Ai to be the point obtained from i applications of the translation S to A0, so Ai = Si(A0). The set of vertices Ai with i any integer, together with edges connecting adjacent vertices, is a sequence of equal-length segments of a line, and is called the regular apeirogon as defined by H. S. M. Coxeter.[1]
A regular apeirogon can be defined as a partition of the Euclidean line E1 into infinitely many equal-length segments. It generalizes the regular n-gon, which may be defined as a partition of the circle S1 into finitely many equal-length segments.[2]
Modern abstract definition
An abstract polytope is a partially ordered set P (whose elements are called faces) with properties modeling those of the inclusions of faces of convex polytopes. The rank (or dimension) of an abstract polytope is determined by the length of the maximal ordered chains of its faces, and an abstract polytope of rank n is called an abstract n-polytope.[3]:{{{1}}}
For abstract polytopes of rank 2, this means that: A) the elements of the partially ordered set are sets of vertices with either zero vertex (the empty set), one vertex, two vertices (an edge), or the entire vertex set (a two-dimensional face), ordered by inclusion of sets; B) each vertex belongs to exactly two edges; C) the undirected graph formed by the vertices and edges is connected.[3]:{{{1}}}[4]:{{{1}}}
An abstract polytope is called an abstract apeirotope if it has infinitely many elements; an abstract 2-apeirotope is called an abstract apeirogon.[3]:{{{1}}}
In an abstract polytope, a flag is a collection of one face of each dimension, all incident to each other (that is, comparable in the partial order); an abstract polytope is called regular if it has symmetries (structure-preserving permutations of its elements) that take any flag to any other flag. In the case of a two-dimensional abstract polytope, this is automatically true; the symmetries of the apeirogon form the infinite dihedral group.[3]:{{{1}}}
Pseudogon
The regular pseudogon is a partition of the hyperbolic line H1 (instead of the Euclidean line) into segments of length 2λ, as an analogue of the regular apeirogon.[2]
Realizations
Definition
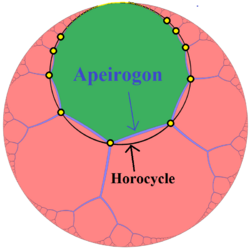
A realization of an abstract apeirogon is defined as a mapping from its vertices to a finite-dimensional geometric space (typically a Euclidean space) such that every symmetry of the abstract apeirogon corresponds to an isometry of the images of the mapping.[3]:{{{1}}}[4]:{{{1}}} Two realizations are called congruent if the natural bijection between their sets of vertices is induced by an isometry of their ambient Euclidean spaces.[3]:{{{1}}}[4]:{{{1}}} The classical definition of an apeirogon as an equally-spaced subdivision of the Euclidean line is a realization in this sense, as is the convex subset in the hyperbolic plane formed by the convex hull of equally-spaced points on a horocycle. Other realizations are possible in higher-dimensional spaces.
Symmetries of a realization
The infinite dihedral group G of symmetries of a realization V of an abstract apeirogon P is generated by two reflections, the product of which translates each vertex of P to the next.[3]:{{{1}}}[4]:{{{1}}} The product of the two reflections can be decomposed as a product of a non-zero translation, finitely many rotations, and a possibly trivial reflection.[3]:{{{1}}}[4]:{{{1}}}
Moduli space of realizations
Generally, the moduli space of realizations of an abstract polytope is a convex cone of infinite dimension.[3]:{{{1}}}[4]:{{{1}}} The realization cone of the abstract apeirogon has uncountably infinite algebraic dimension and cannot be closed in the Euclidean topology.[3]:{{{1}}}[4]:{{{1}}}
Classification of Euclidean apeirogons
The realizations of two-dimensional abstract polytopes (including both polygons and apeirogons), in Euclidean spaces of at most three dimensions, can be classified into six types:
- convex polygons,
- star polygons,
- regular apeirogons in the Euclidean line,
- infinite skew polygons (infinite zig-zag polygons in the Euclidean plane),
- antiprisms (including star prisms and star antiprisms), and
- infinite helical polygons (evenly spaced points along a helix).[5]
Abstract apeirogons may be realized in all of these ways, in some cases mapping infinitely many different vertices of an abstract apeirogon onto finitely many points of the realization. An apeirogon also admits star polygon realizations and antiprismatic realizations with a non-discrete set of infinitely many points.
Generalizations
Higher dimension
Apeirohedra are the 3-dimensional analogues of apeirogons, and are the infinite analogues of polyhedra.[6] More generally, n-apeirotopes or infinite n-polytopes are the n-dimensional analogues of apeirogons, and are the infinite analogues of n-polytopes.[3]:{{{1}}}
See also
- Apeirogonal tiling
- Apeirogonal prism
- Apeirogonal antiprism
- Teragon, a fractal generalized polygon that also has infinitely many sides
References
- ↑ 1.0 1.1 Coxeter, H. S. M. (1948). Regular polytopes. London: Methuen & Co. Ltd.. p. 45.
- ↑ 2.0 2.1 Johnson, Norman W. (2018). "11: Finite Symmetry Groups". Geometries and transformations. Cambridge University Press. p. 226. ISBN 9781107103405. https://books.google.com/books?id=J7NavgAACAAJ.
- ↑ 3.00 3.01 3.02 3.03 3.04 3.05 3.06 3.07 3.08 3.09 3.10 McMullen, Peter; Schulte, Egon (December 2002). [1] Abstract Regular Polytopes] (1st ed.). Cambridge University Press. ISBN 0-521-81496-0. https://archive.org/details/abstractregularp0000mcmu].
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 McMullen, Peter (1994), "Realizations of regular apeirotopes", Aequationes Mathematicae 47 (2–3): 223–239, doi:10.1007/BF01832961
- ↑ Grünbaum, B. (1977). "Regular polyhedra – old and new". Aequationes Mathematicae 16 (1–2): 119. doi:10.1007/BF01836414.
- ↑ Coxeter, H. S. M. (1937). "Regular Skew Polyhedra in Three and Four Dimensions.". Proc. London Math. Soc. 43: 33–62.
External links
- Russell, Robert A.. "Apeirogon". http://mathworld.wolfram.com/Apeirogon.html.
- Olshevsky, George. "Apeirogon". Glossary for Hyperspace. Archived from the original on 4 February 2007. https://web.archive.org/web/20070204075028/members.aol.com/Polycell/glossary.html#Apeirogon.
 |