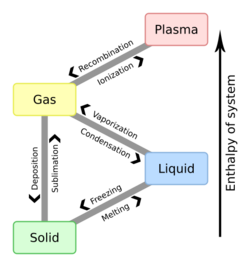
Critical point (thermodynamics)

From HandWiki
Revision as of 23:19, 6 February 2024 by WikiGary (talk | contribs) (simplify)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Temperature and pressure point where phase boundaries disappear
  1. Subcritical ethane, liquid and gas phase coexist.
  2. Critical point (32.17 °C, 48.72 bar), opalescence.
  3. Supercritical ethane, fluid.[1]

In thermodynamics, a critical point (or critical state) is the end point of a phase equilibrium curve. One example is the liquid–vapor critical point, the end point of the pressure–temperature curve that designates conditions under which a liquid and its vapor can coexist. At higher temperatures, the gas cannot be liquefied by pressure alone. At the critical point, defined by a critical temperature Tc and a critical pressure pc, phase boundaries vanish. Other examples include the liquid–liquid critical points in mixtures, and the ferromagnet–paramagnet transition (Curie temperature) in the absence of an external magnetic field.[2]

Liquid–vapor critical point

Overview

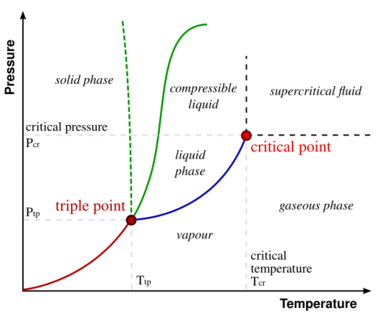
The liquid–vapor critical point in a pressure–temperature phase diagram is at the high-temperature extreme of the liquid–gas phase boundary. The dashed green line shows the anomalous behavior of water.

For simplicity and clarity, the generic notion of critical point is best introduced by discussing a specific example, the vapor–liquid critical point. This was the first critical point to be discovered, and it is still the best known and most studied one.

The figure to the right shows the schematic P-T diagram of a pure substance (as opposed to mixtures, which have additional state variables and richer phase diagrams, discussed below). The commonly known phases solid, liquid and vapor are separated by phase boundaries, i.e. pressure–temperature combinations where two phases can coexist. At the triple point, all three phases can coexist. However, the liquid–vapor boundary terminates in an endpoint at some critical temperature Tc and critical pressure pc. This is the critical point.

The critical point of water occurs at 647.096 K (373.946 °C; 705.103 °F) and 22.064 megapascals (3,200.1 psi; 217.75 atm; 220.64 bar).[3]

In the vicinity of the critical point, the physical properties of the liquid and the vapor change dramatically, with both phases becoming even more similar. For instance, liquid water under normal conditions is nearly incompressible, has a low thermal expansion coefficient, has a high dielectric constant, and is an excellent solvent for electrolytes. Near the critical point, all these properties change into the exact opposite: water becomes compressible, expandable, a poor dielectric, a bad solvent for electrolytes, and mixes more readily with nonpolar gases and organic molecules.[4]

At the critical point, only one phase exists. The heat of vaporization is zero. There is a stationary inflection point in the constant-temperature line (critical isotherm) on a PV diagram. This means that at the critical point:[5][6][7]

[math]\displaystyle{ \left(\frac{\partial p}{\partial V}\right)_T = 0, }[/math]
[math]\displaystyle{ \left(\frac{\partial^2p}{\partial V^2}\right)_T = 0. }[/math]
Isotherms of a gas. The red line is the critical isotherm, with critical point K. The dashed lines represent parts of isotherms which are forbidden since the gradient would be positive, giving the gas in this region a negative compressibility.

Above the critical point there exists a state of matter that is continuously connected with (can be transformed without phase transition into) both the liquid and the gaseous state. It is called supercritical fluid. The common textbook knowledge that all distinction between liquid and vapor disappears beyond the critical point has been challenged by Fisher and Widom,[8] who identified a p–T line that separates states with different asymptotic statistical properties (Fisher–Widom line).

Sometimes[ambiguous] the critical point does not manifest in most thermodynamic or mechanical properties, but is "hidden" and reveals itself in the onset of inhomogeneities in elastic moduli, marked changes in the appearance and local properties of non-affine droplets, and a sudden enhancement in defect pair concentration.[9]

History

Critical carbon dioxide exuding fog while cooling from supercritical to critical temperature.

The existence of a critical point was first discovered by Charles Cagniard de la Tour in 1822[10][11] and named by Dmitri Mendeleev in 1860[12][13] and Thomas Andrews in 1869.[14] Cagniard showed that CO2 could be liquefied at 31 °C at a pressure of 73 atm, but not at a slightly higher temperature, even under pressures as high as 3000 atm.

Theory

Solving the above condition [math]\displaystyle{ (\partial p / \partial V)_T = 0 }[/math] for the van der Waals equation, one can compute the critical point as[5]

[math]\displaystyle{ T_\text{c} = \frac{8a}{27Rb}, \quad V_\text{c} = 3nb, \quad p_\text{c} = \frac{a}{27b^2}. }[/math]

However, the van der Waals equation, based on a mean-field theory, does not hold near the critical point. In particular, it predicts wrong scaling laws.

To analyse properties of fluids near the critical point, reduced state variables are sometimes defined relative to the critical properties[15]

[math]\displaystyle{ T_\text{r} = \frac{T}{T_\text{c}}, \quad p_\text{r} = \frac{p}{p_\text{c}}, \quad V_\text{r} = \frac{V}{RT_\text{c} / p_\text{c}}. }[/math]

The principle of corresponding states indicates that substances at equal reduced pressures and temperatures have equal reduced volumes. This relationship is approximately true for many substances, but becomes increasingly inaccurate for large values of pr.

For some gases, there is an additional correction factor, called Newton's correction, added to the critical temperature and critical pressure calculated in this manner. These are empirically derived values and vary with the pressure range of interest.[16]

Table of liquid–vapor critical temperature and pressure for selected substances

Substance[17][18] Critical temperature Critical pressure (absolute)
Argon 0150.8 −122.4 °C (150.8 K)


0048.1 48.1 atm (4,870 kPa)


Ammonia (NH3)[19] 0405.6 132.4 °C (405.5 K)


0111.3 111.3 atm (11,280 kPa)


R-134a 0374 101.06 °C (374.21 K)


0040 40.06 atm (4,059 kPa)


R-410A 0346 72.8 °C (345.9 K)


0047 47.08 atm (4,770 kPa)


Bromine 0584.0 310.8 °C (584.0 K)


0102 102 atm (10,300 kPa)


Caesium 1938.00 1,664.85 °C (1,938.00 K)


0094 94 atm (9,500 kPa)


Chlorine 0417.0 143.8 °C (416.9 K)


0076.0 76.0 atm (7,700 kPa)


Ethane (C2H6) 0305.2 31.17 °C (304.32 K)


0048.077 48.077 atm (4,871.4 kPa)


Ethanol (C2H5OH) 0514.0 241 °C (514 K)


0062.2 62.18 atm (6,300 kPa)


Fluorine 0144.30 −128.85 °C (144.30 K)


0051.5 51.5 atm (5,220 kPa)


Helium 0005.19 −267.96 °C (5.19 K)


0002.24 2.24 atm (227 kPa)


Hydrogen 0033.20 −239.95 °C (33.20 K)


0012.8 12.8 atm (1,300 kPa)


Krypton 0209.4 −63.8 °C (209.3 K)


0054.3 54.3 atm (5,500 kPa)


Methane (CH4) 0190.8 −82.3 °C (190.8 K)


0045.79 45.79 atm (4,640 kPa)


Neon 0044.40 −228.75 °C (44.40 K)


0027.2 27.2 atm (2,760 kPa)


Nitrogen 0126.3 −146.9 °C (126.2 K)


0033.5 33.5 atm (3,390 kPa)


Oxygen (O2) 0154.6 −118.6 °C (154.6 K)


0049.8 49.8 atm (5,050 kPa)


Carbon dioxide (CO2) 0304.19 31.04 °C (304.19 K)


0072.8 72.8 atm (7,380 kPa)


Nitrous oxide (N2O) 0304.19 36.4 °C (309.5 K)


0072.8 71.5 atm (7,240 kPa)


Sulfuric acid (H2SO4) 0927 654 °C (927 K)


0045.4 45.4 atm (4,600 kPa)


Xenon 0289.8 16.6 °C (289.8 K)


0057.6 57.6 atm (5,840 kPa)


Lithium 3223 2,950 °C (3,220 K)


0652 652 atm (66,100 kPa)


Mercury 1750.1 1,476.9 °C (1,750.1 K)


1720 1,720 atm (174,000 kPa)


Sulfur 1314.00 1,040.85 °C (1,314.00 K)


0207 207 atm (21,000 kPa)


Iron 8500 8,227 °C (8,500 K)


Gold 7250 6,977 °C (7,250 K)


5000 5,000 atm (510,000 kPa)


Aluminium 7850 7,577 °C (7,850 K)


Water (H2O)[3][20] 0647.096 373.946 °C (647.096 K)


0217.7 217.7 atm (22,060 kPa)


Mixtures: liquid–liquid critical point

A plot of typical polymer solution phase behavior including two critical points: a LCST and an UCST

The liquid–liquid critical point of a solution, which occurs at the critical solution temperature, occurs at the limit of the two-phase region of the phase diagram. In other words, it is the point at which an infinitesimal change in some thermodynamic variable (such as temperature or pressure) leads to separation of the mixture into two distinct liquid phases, as shown in the polymer–solvent phase diagram to the right. Two types of liquid–liquid critical points are the upper critical solution temperature (UCST), which is the hottest point at which cooling induces phase separation, and the lower critical solution temperature (LCST), which is the coldest point at which heating induces phase separation.

Mathematical definition

From a theoretical standpoint, the liquid–liquid critical point represents the temperature–concentration extremum of the spinodal curve (as can be seen in the figure to the right). Thus, the liquid–liquid critical point in a two-component system must satisfy two conditions: the condition of the spinodal curve (the second derivative of the free energy with respect to concentration must equal zero), and the extremum condition (the third derivative of the free energy with respect to concentration must also equal zero or the derivative of the spinodal temperature with respect to concentration must equal zero).

See also


References

  1. ↑ Horstmann, Sven (2000). Theoretische und experimentelle Untersuchungen zum Hochdruckphasengleichgewichtsverhalten fluider Stoffgemische für die Erweiterung der PSRK-Gruppenbeitragszustandsgleichung [Theoretical and experimental investigations of the high-pressure phase equilibrium behavior of fluid mixtures for the expansion of the PSRK group contribution equation of state] (Ph.D.) (in Deutsch). Oldenburg, Germany: Carl-von-Ossietzky Universität Oldenburg. ISBN 3-8265-7829-5. OCLC 76176158.
  2. ↑ Stanley, H. Eugene (1987). Introduction to phase transitions and critical phenomena. New York: Oxford University Press. ISBN 0-19-505316-8. OCLC 15696711. https://www.worldcat.org/oclc/15696711. 
  3. ↑ 3.0 3.1 Wagner, W.; Pruß, A. (June 2002). "The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use". Journal of Physical and Chemical Reference Data 31 (2): 398. doi:10.1063/1.1461829. 
  4. ↑ Anisimov, Sengers, Levelt Sengers (2004): Near-critical behavior of aqueous systems. Chapter 2 in Aqueous System at Elevated Temperatures and Pressures Palmer et al., eds. Elsevier.
  5. ↑ 5.0 5.1 P. Atkins and J. de Paula, Physical Chemistry, 8th ed. (W. H. Freeman 2006), p. 21.
  6. ↑ K. J. Laidler and J. H. Meiser, Physical Chemistry (Benjamin/Cummings 1982), p. 27.
  7. ↑ P. A. Rock, Chemical Thermodynamics (MacMillan 1969), p. 123.
  8. ↑ Fisher, Michael E.; Widom, B. (1969). "Decay of Correlations in Linear Systems". Journal of Chemical Physics 50 (9): 3756. doi:10.1063/1.1671624. Bibcode: 1969JChPh..50.3756F. https://aip.scitation.org/doi/abs/10.1063/1.1671624. Retrieved 9 January 2023. 
  9. ↑ Das, Tamoghna; Ganguly, Saswati; Sengupta, Surajit; Rao, Madan (3 June 2015). "Pre-Yield Non-Affine Fluctuations and A Hidden Critical Point in Strained Crystals". Scientific Reports 5 (1): 10644. doi:10.1038/srep10644. PMID 26039380. Bibcode: 2015NatSR...510644D. 
  10. ↑ Charles Cagniard de la Tour (1822). "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que l'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée" (in fr). Annales de Chimie et de Physique 21: 127–132. https://books.google.com/books?id=rzNCAAAAcAAJ&q=Cagniard&pg=PA127. 
  11. ↑ Berche, B., Henkel, M., Kenna, R (2009) Critical phenomena: 150 years since Cagniard de la Tour. Journal of Physical Studies 13 (3), pp. 3001-1–3001-4.
  12. ↑ Mendeleev called the critical point the "absolute temperature of boiling" (Russian: абсолютная температура кипения; German: absolute Siedetemperatur).
  13. ↑ Landau, Lifshitz, Theoretical Physics, Vol. V: Statistical Physics, Ch. 83 [German edition 1984].
  14. ↑ Andrews, Thomas (1869). "The Bakerian lecture: On the continuity of the gaseous and liquid states of matter". Philosophical Transactions of the Royal Society (London) 159: 575–590. doi:10.1098/rstl.1869.0021. http://rstl.royalsocietypublishing.org/content/159/575.full.pdf+html.  The term "critical point" appears on page 588.
  15. ↑ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach. Boston: McGraw-Hill. pp. 91–93. ISBN 978-0-07-121688-3. 
  16. ↑ Maslan, Frank D.; Littman, Theodore M. (1953). "Compressibility Chart for Hydrogen and Inert Gases". Ind. Eng. Chem. 45 (7): 1566–1568. doi:10.1021/ie50523a054. 
  17. ↑ Emsley, John (1991). The Elements (Second ed.). Oxford University Press. ISBN 978-0-19-855818-7. 
  18. ↑ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: An Engineering Approach (Fourth ed.). McGraw-Hill. pp. 824. ISBN 978-0-07-238332-4. https://archive.org/details/thermodynamicsen00ceng_0/page/824. 
  19. ↑ "Ammonia – NH3 – Thermodynamic Properties". http://www.engineeringtoolbox.com/ammonia-d_971.html. 
  20. ↑ "Critical Temperature and Pressure". Purdue University. http://www.chem.purdue.edu/gchelp/liquids/critical.html. 

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Critical_point_(thermodynamics)&oldid=3387361"