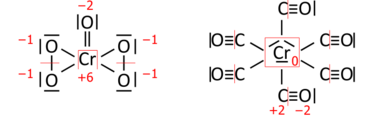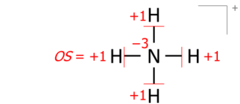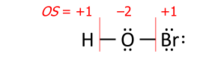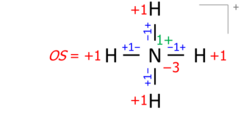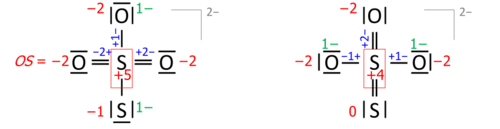Chemistry:Oxidation state

Short description: Hypothetical charge of an atom if all its bonds to different atoms were fully ionic

In chemistry, the oxidation state, or oxidation number, is the hypothetical charge of an atom if all of its bonds to other atoms were fully ionic. It describes the degree of oxidation (loss of electrons) of an atom in a chemical compound. Conceptually, the oxidation state may be positive, negative or zero. While fully ionic bonds are not found in nature, many bonds exhibit strong ionicity, making oxidation state a useful predictor of charge.

The oxidation state of an atom does not represent the "real" charge on that atom, or any other actual atomic property. This is particularly true of high oxidation states, where the ionization energy required to produce a multiply positive ion is far greater than the energies available in chemical reactions. Additionally, the oxidation states of atoms in a given compound may vary depending on the choice of electronegativity scale used in their calculation. Thus, the oxidation state of an atom in a compound is purely a formalism. It is nevertheless important in understanding the nomenclature conventions of inorganic compounds. Also, several observations regarding chemical reactions may be explained at a basic level in terms of oxidation states.

Oxidation states are typically represented by integers which may be positive, zero, or negative. In some cases, the average oxidation state of an element is a fraction, such as 8/3 for iron in magnetite Fe
3O
4 (see below). The highest known oxidation state is reported to be +9, displayed by iridium in the tetroxoiridium(IX) cation (IrO+
4). It is predicted that even a +10 oxidation state may be achieved by platinum in tetroxoplatinum(X), PtO2+
4. The lowest oxidation state is −5, as for boron in Al
3BC and gallium in pentamagnesium digallide (Mg
5Ga
2).

In inorganic nomenclature, the oxidation state is represented by a Roman numeral placed after the element name inside parentheses or as a superscript after the element symbol, e.g. Iron(III) oxide.

The term oxidation was first used by Antoine Lavoisier to signify the reaction of a substance with oxygen. Much later, it was realized that the substance, upon being oxidized, loses electrons, and the meaning was extended to include other reactions in which electrons are lost, regardless of whether oxygen was involved. The increase in the oxidation state of an atom, through a chemical reaction, is known as oxidation; a decrease in oxidation state is known as a reduction. Such reactions involve the formal transfer of electrons: a net gain in electrons being a reduction, and a net loss of electrons being oxidation. For pure elements, the oxidation state is zero.

IUPAC definition

IUPAC has published a "Comprehensive definition of the term oxidation state (IUPAC Recommendations 2016)". It is a distillation of an IUPAC technical report "Toward a comprehensive definition of oxidation state" from 2014. The current IUPAC Gold Book definition of oxidation state is:

Oxidation state of an atom is the charge of this atom after ionic approximation of its heteronuclear bonds...

and the term oxidation number is nearly synonymous.

The underlying principle is that the ionic charge is "the oxidation state of an atom, after ionic approximation of its bonds", where ionic approximation means, hypothesizing that all bonds are ionic. Several criteria were considered for the ionic approximation:

1. Extrapolation of the bond's polarity;
   1. from the electronegativity difference,
   2. from the dipole moment, and
   3. from quantum‐chemical calculations of charges.
2. Assignment of electrons according to the atom's contribution to the bonding Molecular orbital (MO)/ the electron's allegiance in a LCAO–MO model.

In a bond between two different elements, the bond's electrons are assigned to its main atomic contributor/higher electronegativity; in a bond between two atoms of the same element, the electrons are divided equally. This is because most electronegativity scales depend on the atom's bonding state, which makes the assignment of the oxidation state a somewhat circular argument. For example, some scales may turn out unusual oxidation states, such as -6 for platinum in PtH2−
4, for Pauling and Mulliken scales. The dipole moments would, sometimes, also turn out abnormal oxidation numbers, such as in CO and NO, which are oriented with their positive end towards oxygen. Therefore, this leaves the atom's contribution to the bonding MO, the atomic-orbital energy, and from quantum-chemical calculations of charges, as the only viable criteria with cogent values for ionic approximation. However, for a simple estimate for the ionic approximation, we can use Allen electronegativities, as only that electronegativity scale is truly independent of the oxidation state, as it relates to the average valence‐electron energy of the free atom:

Electronegativity using the Allen scale
Group →	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
↓ Period
1	H 2.300																	He 4.160
2	Li 0.912	Be 1.576											B 2.051	C 2.544	N 3.066	O 3.610	F 4.193	Ne 4.787
3	Na 0.869	Mg 1.293											Al 1.613	Si 1.916	P 2.253	S 2.589	Cl 2.869	Ar 3.242
4	K 0.734	Ca 1.034	Sc 1.19	Ti 1.38	V 1.53	Cr 1.65	Mn 1.75	Fe 1.80	Co 1.84	Ni 1.88	Cu 1.85	Zn 1.59	Ga 1.756	Ge 1.994	As 2.211	Se 2.424	Br 2.685	Kr 2.966
5	Rb 0.706	Sr 0.963	Y 1.12	Zr 1.32	Nb 1.41	Mo 1.47	Tc 1.51	Ru 1.54	Rh 1.56	Pd 1.58	Ag 1.87	Cd 1.52	In 1.656	Sn 1.824	Sb 1.984	Te 2.158	I 2.359	Xe 2.582
6	Cs 0.659	Ba 0.881	Lu 1.09	Hf 1.16	Ta 1.34	W 1.47	Re 1.60	Os 1.65	Ir 1.68	Pt 1.72	Au 1.92	Hg 1.76	Tl 1.789	Pb 1.854	Bi 2.01	Po 2.19	At 2.39	Rn 2.60
7	Fr 0.67	Ra 0.89
See also: Electronegativities of the elements (data page)

Determination

While introductory levels of chemistry teaching use postulated oxidation states, the IUPAC recommendation and the Gold Book entry list two entirely general algorithms for the calculation of the oxidation states of elements in chemical compounds.

Simple approach without bonding considerations

Introductory chemistry uses postulates: the oxidation state for an element in a chemical formula is calculated from the overall charge and postulated oxidation states for all the other atoms.

A simple example is based on two postulates,

1. OS = +1 for hydrogen
2. OS = −2 for oxygen

where OS stands for oxidation state. This approach yields correct oxidation states in oxides and hydroxides of any single element, and in acids such as sulfuric acid (H
2SO
4) or dichromic acid (H
2Cr
2O
7). Its coverage can be extended either by a list of exceptions or by assigning priority to the postulates. The latter works for hydrogen peroxide (H
2O
2) where the priority of rule 1 leaves both oxygens with oxidation state −1.

Additional postulates and their ranking may expand the range of compounds to fit a textbook's scope. As an example, one postulatory algorithm from many possible; in a sequence of decreasing priority:

1. An element in a free form has OS = 0.
2. In a compound or ion, the sum of the oxidation states equals the total charge of the compound or ion.
3. Fluorine in compounds has OS = −1; this extends to chlorine and bromine only when not bonded to a lighter halogen, oxygen or nitrogen.
4. Group 1 and group 2 metals in compounds have OS = +1 and +2, respectively.
5. Hydrogen has OS = +1 but adopts −1 when bonded as a hydride to metals or metalloids.
6. Oxygen in compounds has OS = −2 but only when not bonded to oxygen (e.g. in peroxides) or fluorine.

This set of postulates covers oxidation states of fluorides, chlorides, bromides, oxides, hydroxides, and hydrides of any single element. It covers all oxoacids of any central atom (and all their fluoro-, chloro-, and bromo-relatives), as well as salts of such acids with group 1 and 2 metals. It also covers iodides, sulfides, and similar simple salts of these metals.

Algorithm of assigning bonds

This algorithm is performed on a Lewis structure (a diagram that shows all valence electrons). Oxidation state equals the charge of an atom after each of its heteronuclear bonds has been assigned to the more-electronegative partner of the bond (except when that partner is a reversibly bonded Lewis-acid ligand) and homonuclear bonds have been divided equally:

where each "—" represents an electron pair (either shared between two atoms or solely on one atom), and "OS" is the oxidation state as a numerical variable.

After the electrons have been assigned according to the vertical red lines on the formula, the total number of valence electrons that now "belong" to each atom is subtracted from the number N of valence electrons of the neutral atom (such as 5 for nitrogen in group 15) to yield that atom's oxidation state.

This example shows the importance of describing the bonding. Its summary formula, HNO
3, corresponds to two structural isomers; the peroxynitrous acid in the above figure and the more stable nitric acid. With the formula HNO
3, the simple approach without bonding considerations yields −2 for all three oxygens and +5 for nitrogen, which is correct for nitric acid. For the peroxynitrous acid, however, the two oxygens in the O–O bond each has OS = −1 and the nitrogen has OS = +3, which requires a structure to understand.

Organic compounds are treated in a similar manner; exemplified here on functional groups occurring in between methane (CH
4) and carbon dioxide (CO
2):

Analogously for transition-metal compounds; CrO(O
2)
2 on the left has a total of 36 valence electrons (18 pairs to be distributed), and hexacarbonylchromium (Cr(CO)
6) on the right has 66 valence electrons (33 pairs):

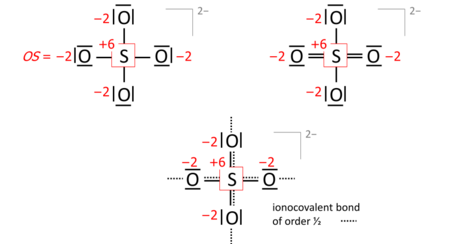
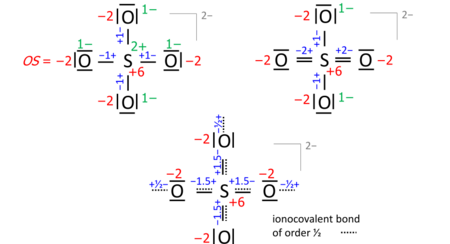
A key step is drawing the Lewis structure of the molecule (neutral, cationic, anionic): atom symbols are arranged so that pairs of atoms can be joined by single two-electron bonds as in the molecule (a sort of "skeletal" structure), and the remaining valence electrons are distributed such that sp atoms obtain an octet (duet for hydrogen) with a priority that increases in proportion with electronegativity. In some cases, this leads to alternative formulae that differ in bond orders (the full set of which is called the resonance formulas). Consider the sulfate anion (SO2−
4) with 32 valence electrons; 24 from oxygens, 6 from sulfur, 2 of the anion charge obtained from the implied cation). The bond orders to the terminal oxygens do not affect the oxidation state so long as the oxygens have octets. Already the skeletal structure, top left, yields the correct oxidation states, as does the Lewis structure, top right (one of the resonance formulas):

The bond-order formula at the bottom is closest to the reality of four equivalent oxygens each having a total bond order of 2. That total includes the bond of order 1/2 to the implied cation and follows the 8 – N rule requiring that the main-group atom's bond order equals 8 – N valence electrons of the neutral atom, enforced with a priority that proportionately increases with electronegativity.

This algorithm works equally for molecular cations composed of several atoms. An example is the ammonium cation of 8 valence electrons (5 from nitrogen, 4 from hydrogens, minus 1 electron for the cation's positive charge):

Drawing Lewis structures with electron pairs as dashes emphasizes the essential equivalence of bond pairs and lone pairs when counting electrons and moving bonds onto atoms. Structures drawn with electron dot pairs are of course identical in every way:

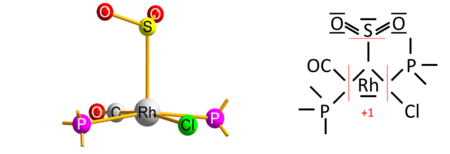
The algorithm's caveat

The algorithm contains a caveat, which concerns rare cases of transition-metal complexes with a type of ligand that is reversibly bonded as a Lewis acid (as an acceptor of the electron pair from the transition metal); termed a "Z-type" ligand in Green's covalent bond classification method. The caveat originates from the simplifying use of electronegativity instead of the MO-based electron allegiance to decide the ionic sign. One early example is the O
2S–RhCl(CO)(PPh
3)
2 complex with sulfur dioxide (SO
2) as the reversibly-bonded acceptor ligand (released upon heating). The Rh−S bond is therefore extrapolated ionic against Allen electronegativities of rhodium and sulfur, yielding oxidation state +1 for rhodium:

Algorithm of summing bond orders

This algorithm works on Lewis structures and bond graphs of extended (non-molecular) solids:

Oxidation state is obtained by summing the heteronuclear-bond orders at the atom as positive if that atom is the electropositive partner in a particular bond and as negative if not, and the atom’s formal charge (if any) is added to that sum.

Applied to a Lewis structure

An example of a Lewis structure with no formal charge,

illustrates that, in this algorithm, homonuclear bonds are simply ignored (the bond orders are in blue).

Carbon monoxide exemplifies a Lewis structure with formal charges:

To obtain the oxidation states, the formal charges are summed with the bond-order value taken positively at the carbon and negatively at the oxygen.

Applied to molecular ions, this algorithm considers the actual location of the formal (ionic) charge, as drawn in the Lewis structure. As an example, summing bond orders in the ammonium cation yields −4 at the nitrogen of formal charge +1, with the two numbers adding to the oxidation state of −3:

The sum of oxidation states in the ion equals its charge (as it equals zero for a neutral molecule).

Also in anions, the formal (ionic) charges have to be considered when nonzero. For sulfate this is exemplified with the skeletal or Lewis structures (top), compared with the bond-order formula of all oxygens equivalent and fulfilling the octet and 8 − N rules (bottom):

Applied to bond graph

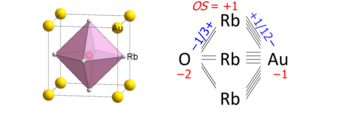
A bond graph in solid-state chemistry is a chemical formula of an extended structure, in which direct bonding connectivities are shown. An example is the AuORb
3 perovskite, the unit cell of which is drawn on the left and the bond graph (with added numerical values) on the right:

We see that the oxygen atom bonds to the six nearest rubidium cations, each of which has 4 bonds to the auride anion. The bond graph summarizes these connectivities. The bond orders (also called bond valences) sum up to oxidation states according to the attached sign of the bond's ionic approximation (there are no formal charges in bond graphs).

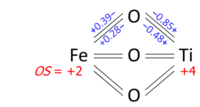
Determination of oxidation states from a bond graph can be illustrated on ilmenite, FeTiO
3. We may ask whether the mineral contains Fe²⁺ and Ti⁴⁺, or Fe³⁺ and Ti³⁺. Its crystal structure has each metal atom bonded to six oxygens and each of the equivalent oxygens to two irons and two titaniums, as in the bond graph below. Experimental data show that three metal-oxygen bonds in the octahedron are short and three are long (the metals are off-center). The bond orders (valences), obtained from the bond lengths by the bond valence method, sum up to 2.01 at Fe and 3.99 at Ti; which can be rounded off to oxidation states +2 and +4, respectively:

Balancing redox

Oxidation states can be useful for balancing chemical equations for oxidation-reduction (or redox) reactions, because the changes in the oxidized atoms have to be balanced by the changes in the reduced atoms. For example, in the reaction of acetaldehyde with Tollens' reagent to form acetic acid (shown below), the carbonyl carbon atom changes its oxidation state from +1 to +3 (loses two electrons). This oxidation is balanced by reducing two Ag+
cations to Ag0
(gaining two electrons in total).

An inorganic example is the Bettendorf reaction using tin dichloride (SnCl
2) to prove the presence of arsenite ions in a concentrated HCl extract. When arsenic(III) is present, a brown coloration appears forming a dark precipitate of arsenic, according to the following simplified reaction:

[math]\ce{ 2 As^3+ + 3 Sn^2+ -> 2 As^0 + 3 Sn^4+ }[/math]

Here three tin atoms are oxidized from oxidation state +2 to +4, yielding six electrons that reduce two arsenic atoms from oxidation state +3 to 0. The simple one-line balancing goes as follows: the two redox couples are written down as they react;

[math]\ce{ As^3+ + Sn^2+ <=> As^0 + Sn^4+ }[/math]

One tin is oxidized from oxidation state +2 to +4, a two-electron step, hence 2 is written in front of the two arsenic partners. One arsenic is reduced from +3 to 0, a three-electron step, hence 3 goes in front of the two tin partners. An alternative three-line procedure is to write separately the half-reactions for oxidation and reduction, each balanced with electrons, and then to sum them up such that the electrons cross out. In general, these redox balances (the one-line balance or each half-reaction) need to be checked for the ionic and electron charge sums on both sides of the equation being indeed equal. If they are not equal, suitable ions are added to balance the charges and the non-redox elemental balance.

Appearances

Nominal oxidation states

A nominal oxidation state is a general term with two different definitions:

• Electrochemical oxidation state represents a molecule or ion in the Latimer diagram or Frost diagram for its redox-active element. An example is the Latimer diagram for sulfur at pH 0 where the electrochemical oxidation state +2 for sulfur puts HS₂O−3 between S and H₂SO₃:

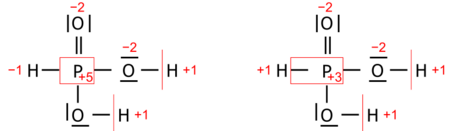
• Systematic oxidation state is chosen from close alternatives as a pedagogical description. An example is the oxidation state of phosphorus in H₃PO₃ (structurally diprotic HPO(OH)₂) taken nominally as +3, while Allen electronegativities of phosphorus and hydrogen suggest +5 by a narrow margin that makes the two alternatives almost equivalent:

Both alternative oxidation numbers for phosphorus make chemical sense, depending on which chemical property or reaction is emphasized. By contrast, a calculated alternative, such as the average (+4) does not.

Ambiguous oxidation states

Lewis formulae are rule-based approximations of chemical reality, as are Allen electronegativities. Still, oxidation states may seem ambiguous when their determination is not straightforward. If only an experiment can determine the oxidation state, the rule-based determination is ambiguous (insufficient). There are also truly dichotomous values that are decided arbitrarily.

Oxidation-state determination from resonance formulas

Seemingly ambiguous oxidation states are derived from a set of resonance formulas of equal weights for a molecule having heteronuclear bonds where the atom connectivity does not correspond to the number of two-electron bonds dictated by the 8 − N rule. An example is S₂N₂ where four resonance formulas featuring one S=N double bond have oxidation states +2 and +4 for the two sulfur atoms, which average to +3 because the two sulfur atoms are equivalent in this square-shaped molecule.

A physical measurement is needed to determine oxidation state

• when a non-innocent ligand is present, of hidden or unexpected redox properties that could otherwise be assigned to the central atom. An example is the nickel dithiolate complex, Ni(S₂C₂H₂)2−2.
• when the redox ambiguity of a central atom and ligand yields dichotomous oxidation states of close stability, thermally induced tautomerism may result, as exemplified by manganese catecholate, Mn(C
  6H
  4O
  2)
  3. Assignment of such oxidation states requires spectroscopic, magnetic or structural data.
• when the bond order has to be ascertained along with an isolated tandem of a heteronuclear and a homonuclear bond. An example is thiosulfate S₂O2−3 having two possible oxidation states (bond orders are in blue and formal charges in green):

The S–S distance measurement in thiosulfate is needed to reveal that this bond order is very close to 1, as in the formula on the left.

Ambiguous/arbitrary oxidation states

• when the electronegativity difference between two bonded atoms is very small (as in H₃PO₃). Two almost equivalent pairs of oxidation states, arbitrarily chosen, are obtained for these atoms.
• when an electronegative p-block atom forms solely homonuclear bonds, the number of which differs from the number of two-electron bonds suggested by rules. Examples are homonuclear finite chains like N−3 (the central nitrogen connects two atoms with four two-electron bonds while only three two-electron bonds are required by 8 − N rule) or I−3 (the central iodine connects two atoms with two two-electron bonds while only one two-electron bond fulfills the 8 − N rule). A sensible approach is to distribute the ionic charge over the two outer atoms. Such a placement of charges in a polysulfide S2−n (where all inner sulfurs form two bonds, fulfilling the 8 − N rule) follows already from its Lewis structure.
• when the isolated tandem of a heteronuclear and a homonuclear bond leads to a bonding compromise in between two Lewis structures of limiting bond orders. An example is N₂O:

The typical oxidation state of nitrogen in N₂O is +1, which also obtains for both nitrogens by a molecular orbital approach. The formal charges on the right comply with electronegativities, which implies an added ionic bonding contribution. Indeed, the estimated N−N and N−O bond orders are 2.76 and 1.9, respectively, approaching the formula of integer bond orders that would include the ionic contribution explicitly as a bond (in green):

Conversely, formal charges against electronegativities in a Lewis structure decrease the bond order of the corresponding bond. An example is carbon monoxide with a bond-order estimate of 2.6.

Fractional oxidation states

Fractional oxidation states are often used to represent the average oxidation state of several atoms of the same element in a structure. For example, the formula of magnetite is Fe₃O₄, implying an average oxidation state for iron of +8/3. However, this average value may not be representative if the atoms are not equivalent. In a Fe₃O₄ crystal below 120 K (−153 °C), two-thirds of the cations are Fe³⁺ and one-third are Fe²⁺, and the formula may be more clearly represented as FeO·Fe₂O₃.

Likewise, propane, C₃H₈, has been described as having a carbon oxidation state of −8/3. Again, this is an average value since the structure of the molecule is H₃C−CH₂−CH₃, with the first and third carbon atoms each having an oxidation state of −3 and the central one −2.

An example with true fractional oxidation states for equivalent atoms is potassium superoxide, KO₂. The diatomic superoxide ion O−2 has an overall charge of −1, so each of its two equivalent oxygen atoms is assigned an oxidation state of −1/2. This ion can be described as a resonance hybrid of two Lewis structures, where each oxygen has an oxidation state of 0 in one structure and −1 in the other.

For the cyclopentadienyl anion C₅H−5, the oxidation state of C is −1 + −1/5 = −6/5. The −1 occurs because each carbon is bonded to one hydrogen atom (a less electronegative element), and the −1/5 because the total ionic charge of −1 is divided among five equivalent carbons. Again this can be described as a resonance hybrid of five equivalent structures, each having four carbons with oxidation state −1 and one with −2.

Examples of fractional oxidation states for carbon

Oxidation state	Example species
−6/5	C5H−5
−6/7	C7H+7
+3/2	C4O2−4

Finally, fractional oxidation numbers are not used in the chemical nomenclature. For example the red lead Pb₃O₄ is represented as lead(II,IV) oxide, showing the oxidation states of the two nonequivalent lead atoms.

Elements with multiple oxidation states

See also § List of oxidation states of the elements

Most elements have more than one possible oxidation state. For example, carbon has nine possible integer oxidation states from −4 to +4:

Integer oxidation states of carbon

Oxidation state	Example compound
−4	CH4
−3	C2H6
−2	C2H4, CH3Cl
−1	C2H2, C6H6, (CH2OH)2
0	HCHO, CH2Cl2
+1	OCHCHO, CHCl2CHCl2
+2	HCOOH, CHCl3
+3	HOOCCOOH, C2Cl6
+4	CCl4, CO2

Oxidation state in metals

Many compounds with luster and electrical conductivity maintain a simple stoichiometric formula, such as the golden TiO, blue-black RuO₂ or coppery ReO₃, all of obvious oxidation state. Ultimately, assigning the free metallic electrons to one of the bonded atoms is not comprehensive and can yield unusual oxidation states. Examples are the LiPb and Cu₃Au ordered alloys, the composition and structure of which are largely determined by atomic size and packing factors. Should oxidation state be needed for redox balancing, it is best set to 0 for all atoms of such an alloy.

List of oxidation states of the elements

This is a list of known oxidation states of the chemical elements, excluding nonintegral values. The most common states appear in bold. The table is based on that of Greenwood and Earnshaw, with additions noted. Every element exists in oxidation state 0 when it is the pure non-ionized element in any phase, whether monatomic or polyatomic allotrope. The column for oxidation state 0 only shows elements known to exist in oxidation state 0 in compounds.

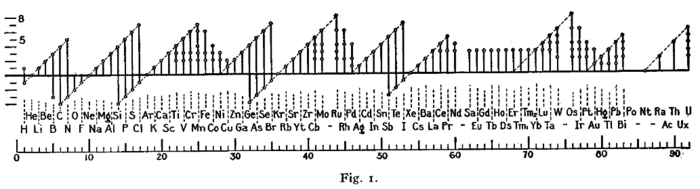
Early forms (octet rule)

A figure with a similar format was used by Irving Langmuir in 1919 in one of the early papers about the octet rule. The periodicity of the oxidation states was one of the pieces of evidence that led Langmuir to adopt the rule.

Use in nomenclature

The oxidation state in compound naming for transition metals and lanthanides and actinides is placed either as a right superscript to the element symbol in a chemical formula, such as Fe^III or in parentheses after the name of the element in chemical names, such as iron(III). For example, Fe₂(SO₄)₃ is named iron(III) sulfate and its formula can be shown as FeIII2(SO₄)₃. This is because a sulfate ion has a charge of −2, so each iron atom takes a charge of +3.

History of the oxidation state concept

Early days

Oxidation itself was first studied by Antoine Lavoisier, who defined it as the result of reactions with oxygen (hence the name). The term has since been generalized to imply a formal loss of electrons. Oxidation states, called oxidation grades by Friedrich Wöhler in 1835, were one of the intellectual stepping stones that Dmitri Mendeleev used to derive the periodic table. William B. Jensen gives an overview of the history up to 1938.

Use in nomenclature

When it was realized that some metals form two different binary compounds with the same nonmetal, the two compounds were often distinguished by using the ending -ic for the higher metal oxidation state and the ending -ous for the lower. For example, FeCl₃ is ferric chloride and FeCl₂ is ferrous chloride. This system is not very satisfactory (although sometimes still used) because different metals have different oxidation states which have to be learned: ferric and ferrous are +3 and +2 respectively, but cupric and cuprous are +2 and +1, and stannic and stannous are +4 and +2. Also, there was no allowance for metals with more than two oxidation states, such as vanadium with oxidation states +2, +3, +4, and +5.

This system has been largely replaced by one suggested by Alfred Stock in 1919 and adopted by IUPAC in 1940. Thus, FeCl₂ was written as iron(II) chloride rather than ferrous chloride. The Roman numeral II at the central atom came to be called the "Stock number" (now an obsolete term), and its value was obtained as a charge at the central atom after removing its ligands along with the electron pairs they shared with it.

Development towards the current concept

The term "oxidation state" in English chemical literature was popularized by Wendell Mitchell Latimer in his 1938 book about electrochemical potentials. He used it for the value (synonymous with the German term Wertigkeit) previously termed "valence", "polar valence" or "polar number" in English, or "oxidation stage" or indeed the "state of oxidation". Since 1938, the term "oxidation state" has been connected with electrochemical potentials and electrons exchanged in redox couples participating in redox reactions. By 1948, IUPAC used the 1940 nomenclature rules with the term "oxidation state", instead of the original valency. In 1948 Linus Pauling proposed that oxidation number could be determined by extrapolating bonds to being completely ionic in the direction of electronegativity. A full acceptance of this suggestion was complicated by the fact that the Pauling electronegativities as such depend on the oxidation state and that they may lead to unusual values of oxidation states for some transition metals. In 1990 IUPAC resorted to a postulatory (rule-based) method to determine the oxidation state. This was complemented by the synonymous term oxidation number as a descendant of the Stock number introduced in 1940 into the nomenclature. However, the terminology using "ligands" gave the impression that oxidation number might be something specific to coordination complexes. This situation and the lack of a real single definition generated numerous debates about the meaning of oxidation state, suggestions about methods to obtain it and definitions of it. To resolve the issue, an IUPAC project (2008-040-1-200) was started in 2008 on the "Comprehensive Definition of Oxidation State", and was concluded by two reports and by the revised entries "Oxidation State" and "Oxidation Number" in the IUPAC Gold Book. The outcomes were a single definition of oxidation state and two algorithms to calculate it in molecular and extended-solid compounds, guided by Allen electronegativities that are independent of oxidation state.

See also

• Electronegativity
• Electrochemistry
• Atomic orbital
• Atomic shell
• Quantum numbers
  • Azimuthal quantum number
  • Principal quantum number
  • Magnetic quantum number
  • Spin quantum number
• Aufbau principle
  • Wiswesser's rule
• Ionization energy
• Electron affinity
• Ionic potential
• Ions
  • Cations and Anions
  • Polyatomic ions
• Covalent bonding
• Metallic bonding
• Hybridization