Elongated bipyramid
From HandWiki
Short description: Polyhedron formed by capping a prism with pyramids
| Elongated bipyramid | |
|---|---|
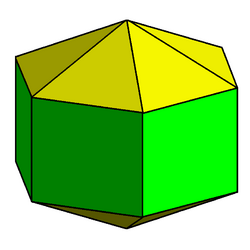 Example: elongated hexagonal bipyramid | |
| Faces | 2n triangles n squares |
| Edges | 5n |
| Vertices | 2n + 2 |
| Symmetry group | Dnh, [n,2], (*n22) |
| Rotation group | Dn, [n,2]+, (n22) |
| Dual polyhedron | bifrustums |
| Properties | convex |
In geometry, the elongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid (by inserting an n-gonal prism between its congruent halves).
There are three elongated bipyramids that are Johnson solids:
- Elongated triangular bipyramid (J14),
- Elongated square bipyramid (J15), and
- Elongated pentagonal bipyramid (J16).
Higher forms can be constructed with isosceles triangles.
Forms
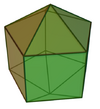
| Name | elongated triangular bipyramid J14 |
elongated square bipyramid J15 |
elongated pentagonal bipyramid J16 |
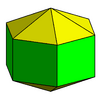
elongated hexagonal bipyramid |
|---|---|---|---|---|
| Type | Equilateral | Irregular | ||
| Image | 
|

|
|
|
| Faces | 6 triangles, 3 squares |
8 triangles, 4 squares |
10 triangles, 5 squares |
12 triangles, 6 squares |
| Dual | triangular bifrustum | square bifrustum | pentagonal bifrustum | hexagonal bifrustum |
Applications
Elongated bipyramids are sometimes used as dice, especially to make dice with atypical side count, such as 5 or 7. Such a die has numbers written on the square faces, which are usually heightened into rectangles for convenience in rolling. Whichever number comes face-up when the die is rolled is the side that is to be read.
See also
References
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
 |

