Hadamard product (matrices)
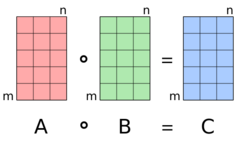
In mathematics, the Hadamard product (also known as the element-wise product, entrywise product[1]:ch. 5 or Schur product[2]) is a binary operation that takes in two matrices of the same dimensions and returns a matrix of the multiplied corresponding elements. This operation can be thought as a "naive matrix multiplication" and is different from the matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard or German mathematician Issai Schur.
The Hadamard product is associative and distributive. Unlike the matrix product, it is also commutative.[3]
Definition
For two matrices A and B of the same dimension m × n, the Hadamard product (sometimes [4][5][6]) is a matrix of the same dimension as the operands, with elements given by[3]
For matrices of different dimensions (m × n and p × q, where m ≠ p or q), the Hadamard product is undefined.
For example, the Hadamard product for two arbitrary 2 × 3 matrices is:
Properties
- The Hadamard product is commutative (when working with a commutative ring), associative and distributive over addition. That is, if A, B, and C are matrices of the same size, and k is a scalar:
- The identity matrix under Hadamard multiplication of two m × n matrices is an m × n matrix where all elements are equal to 1. This is different from the identity matrix under regular matrix multiplication, where only the elements of the main diagonal are equal to 1. Furthermore, a matrix has an inverse under Hadamard multiplication if and only if none of the elements are equal to zero.[7]
- For vectors x and y, and corresponding diagonal matrices Dx and Dy with these vectors as their main diagonals, the following identity holds:[1]:479 where x* denotes the conjugate transpose of x. In particular, using vectors of ones, this shows that the sum of all elements in the Hadamard product is the trace of ABT where superscript T denotes the matrix transpose, that is, . A related result for square A and B, is that the row-sums of their Hadamard product are the diagonal elements of ABT:[8] Similarly, Furthermore, a Hadamard matrix-vector product can be expressed as: where is the vector formed from the diagonals of matrix M.
- The Hadamard product is a principal submatrix of the Kronecker product.[9][10][11]
- The Hadamard product satisfies the rank inequality
- If A and B are positive-definite matrices, then the following inequality involving the Hadamard product holds:[12] where λi(A) is the ith largest eigenvalue of A.
- If D and E are diagonal matrices, then[13]
- The Hadamard product of two vectors and is the same as matrix multiplication of the corresponding diagonal matrix of one vector by the other vector:
- The vector to diagonal matrix operator may be expressed using the Hadamard product as: where is a constant vector with elements and is the identity matrix.
The mixed-product property
where is Kronecker product, assuming has the same dimensions of and with .
where denotes face-splitting product.[14]
where is column-wise Khatri–Rao product.
Schur product theorem
The Hadamard product of two positive-semidefinite matrices is positive-semidefinite.[3][8] This is known as the Schur product theorem,[7] after Russian mathematician Issai Schur. For two positive-semidefinite matrices A and B, it is also known that the determinant of their Hadamard product is greater than or equal to the product of their respective determinants:[8]
Analogous operations
Other Hadamard operations are also seen in the mathematical literature,[15] namely the Hadamard root and Hadamard power (which are in effect the same thing because of fractional indices), defined for a matrix such that:
For
and for
The Hadamard inverse reads:[15]
A Hadamard division is defined as:[16][17]
In programming languages
Most scientific or numerical programming languages include the Hadamard product, under various names.
In MATLAB, the Hadamard product is expressed as "dot multiply": a .* b, or the function call: times(a, b).[18] It also has analogous dot operators which include, for example, the operators a .^ b and a ./ b [19]. Because of this mechanism, it is possible to reserve * and ^ for matrix multiplication and matrix exponentials, respectively.
The programming language Julia has similar syntax as MATLAB, where Hadamard multiplication is called broadcast multiplication and also denoted with a .* b, and other operators are analogously defined element-wise, for example Hadamard powers use a .^ b[20]. But unlike MATLAB, in Julia this "dot" syntax is generalized with a generic broadcasting operator . which can apply any function element-wise. This includes both binary operators (such as the aformentioned multiplication and exponentiation, as well as any other binary operator such as the Kronecker product), and also unary operators such as ! and √. Thus, any function in prefix notation f can be applied as f.(x).[21]
Python does not have built-in array support, leading to inconsistent/conflicting notations. The NumPy numerical library interprets a*b or a.multiply(b) as the Hadamard product, and uses a@b or a.matmul(b) for the matrix product. With the SymPy symbolic library, multiplication of array objects as either a*b or a@b will produce the matrix product. The Hadamard product can be obtained with the method call a.multiply_elementwise(b).[22] Some Python packages include support for Hadamard powers using methods like np.power(a, b), or the Pandas method a.pow(b).
In C++, the Eigen library provides a cwiseProduct member function for the Matrix class (a.cwiseProduct(b)), while the Armadillo library uses the operator % to make compact expressions (a % b; a * b is a matrix product).
In GAUSS, and HP Prime, the operation is known as array multiplication.
In Fortran, R, APL, J and Wolfram Language (Mathematica), the multiplication operator * or × apply the Hadamard product, whereas the matrix product is written using matmul, %*%, +.×, +/ .* and ., respectively.
The R package matrixcalc introduces the function hadamard.prod() for Hadamard Product of numeric matrices or vectors.[23]
Applications
The Hadamard product appears in lossy compression algorithms such as JPEG. The decoding step involves an entry-for-entry product, in other words the Hadamard product.[citation needed]
In image processing, the Hadamard operator can be used for enhancing, suppressing or masking image regions. One matrix represents the original image, the other acts as weight or masking matrix.
It is used in the machine learning literature, for example, to describe the architecture of recurrent neural networks as GRUs or LSTMs.[24]
It is also used to study the statistical properties of random vectors and matrices. [25][26]
The penetrating face product
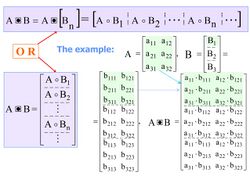
According to the definition of V. Slyusar the penetrating face product of the p×g matrix and n-dimensional matrix (n > 1) with p×g blocks () is a matrix of size of the form:[27]
Example
If
then
Main properties
where denotes the face-splitting product of matrices,
- where is a vector.
Applications
The penetrating face product is used in the tensor-matrix theory of digital antenna arrays.[27] This operation can also be used in artificial neural network models, specifically convolutional layers.[28]
See also
References
- ↑ 1.0 1.1 Horn, Roger A.; Johnson, Charles R. (2012). Matrix analysis. Cambridge University Press.
- ↑ Davis, Chandler (1962). "The norm of the Schur product operation". Numerische Mathematik 4 (1): 343–44. doi:10.1007/bf01386329.
- ↑ 3.0 3.1 3.2 Million, Elizabeth (April 12, 2007). "The Hadamard Product". http://buzzard.ups.edu/courses/2007spring/projects/million-paper.pdf.
- ↑ "Hadamard product - Machine Learning Glossary". https://machinelearning.wtf/terms/hadamard-product/.
- ↑ "linear algebra - What does a dot in a circle mean?". https://math.stackexchange.com/q/815315.
- ↑ "Element-wise (or pointwise) operations notation?". https://math.stackexchange.com/a/601545/688715.
- ↑ 7.0 7.1 Million, Elizabeth. "The Hadamard Product". http://buzzard.ups.edu/courses/2007spring/projects/million-paper.pdf.
- ↑ 8.0 8.1 8.2 Styan, George P. H. (1973), "Hadamard Products and Multivariate Statistical Analysis", Linear Algebra and Its Applications 6: 217–240, doi:10.1016/0024-3795(73)90023-2
- ↑ Liu, Shuangzhe; Trenkler, Götz (2008). "Hadamard, Khatri-Rao, Kronecker and other matrix products". International Journal of Information and Systems Sciences 4 (1): 160–177.
- ↑ Liu, Shuangzhe; Leiva, Víctor; Zhuang, Dan; Ma, Tiefeng; Figueroa-Zúñiga, Jorge I. (2022). "Matrix differential calculus with applications in the multivariate linear model and its diagnostics". Journal of Multivariate Analysis 188: 104849. doi:10.1016/j.jmva.2021.104849.
- ↑ Liu, Shuangzhe; Trenkler, Götz; Kollo, Tõnu; von Rosen, Dietrich; Baksalary, Oskar Maria (2023). "Professor Heinz Neudecker and matrix differential calculus" (in en). Statistical Papers. doi:10.1007/s00362-023-01499-w.
- ↑ Hiai, Fumio; Lin, Minghua (February 2017). "On an eigenvalue inequality involving the Hadamard product". Linear Algebra and Its Applications 515: 313–320. doi:10.1016/j.laa.2016.11.017.
- ↑ "Project". buzzard.ups.edu. 2007. http://buzzard.ups.edu/courses/2007spring/projects/million-paper.pdf.
- ↑ Slyusar, V. I. (1998). "End products in matrices in radar applications.". Radioelectronics and Communications Systems 41 (3): 50–53. http://slyusar.kiev.ua/en/IZV_1998_3.pdf.
- ↑ 15.0 15.1 Reams, Robert (1999). "Hadamard inverses, square roots and products of almost semidefinite matrices". Linear Algebra and Its Applications 288: 35–43. doi:10.1016/S0024-3795(98)10162-3.
- ↑ Wetzstein, Gordon; Lanman, Douglas; Hirsch, Matthew; Raskar, Ramesh. "Supplementary Material: Tensor Displays: Compressive Light Field Synthesis using Multilayer Displays with Directional Backlighting". MIT Media Lab. http://web.media.mit.edu/~gordonw/TensorDisplays/TensorDisplays-Supplement.pdf.
- ↑ Cyganek, Boguslaw (2013). Object Detection and Recognition in Digital Images: Theory and Practice. John Wiley & Sons. p. 109. ISBN 9781118618363. https://books.google.com/books?id=upsxI3bOZvAC&pg=PT109.
- ↑ "MATLAB times function". https://www.mathworks.com/help/matlab/ref/times.html.
- ↑ "Array vs. Matrix Operations". https://www.mathworks.com/help/matlab/matlab_prog/array-vs-matrix-operations.html.
- ↑ "Vectorized "dot" operators". https://docs.julialang.org/en/v1/manual/mathematical-operations/#man-dot-operators.
- ↑ "Dot Syntax for Vectorizing Functions". https://docs.julialang.org/en/v1/manual/functions/#man-vectorized.
- ↑ "Common Matrices — SymPy 1.9 documentation". https://docs.sympy.org/latest/modules/matrices/common.html?highlight=multiply_elementwise#sympy.matrices.common.MatrixCommon.multiply.
- ↑ "Matrix multiplication". An Introduction to R. The R Project for Statistical Computing. 16 May 2013. https://cran.r-project.org/doc/manuals/r-release/R-intro.html#Multiplication.
- ↑ Sak, Haşim; Senior, Andrew; Beaufays, Françoise (2014-02-05). "Long Short-Term Memory Based Recurrent Neural Network Architectures for Large Vocabulary Speech Recognition". arXiv:1402.1128 [cs.NE].
- ↑ Neudecker, Heinz; Liu, Shuangzhe; Polasek, Wolfgang (1995). "The Hadamard product and some of its applications in statistics". Statistics 26 (4): 365–373. doi:10.1080/02331889508802503.
- ↑ Neudecker, Heinz; Liu, Shuangzhe (2001). "Some statistical properties of Hadamard products of random matrices". Statistical Papers 42 (4): 475–487. doi:10.1007/s003620100074.
- ↑ 27.0 27.1 27.2 Slyusar, V. I. (March 13, 1998). "A Family of Face Products of Matrices and its properties". Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz. 1999. 35 (3): 379–384. doi:10.1007/BF02733426. http://slyusar.kiev.ua/FACE.pdf.
- ↑ Ha D., Dai A.M., Le Q.V. (2017). "HyperNetworks.". The International Conference on Learning Representations (ICLR) 2017. – Toulon, 2017.: Page 6.
 |

