Inverse function rule

Short description: Calculus identity

The thick blue curve and the thick red curves are inverse to each other. A thin curve is the derivative of the same colored thick curve. Inverse function rule:
[math]\displaystyle{ {\color{CornflowerBlue}{f'}}(x) = \frac{1}{{\color{Salmon}{(f^{-1})'}}({\color{Blue}{f}}(x))} }[/math]

Example for arbitrary [math]\displaystyle{ x_0 \approx 5.8 }[/math]:
[math]\displaystyle{ {\color{CornflowerBlue}{f'}}(x_0) = \frac{1}{4} }[/math]
[math]\displaystyle{ {\color{Salmon}{(f^{-1})'}}({\color{Blue}{f}}(x_0)) = 4~ }[/math]

In calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function $f$ in terms of the derivative of $f$ . More precisely, if the inverse of [math]\displaystyle{ f }[/math] is denoted as [math]\displaystyle{ f^{-1} }[/math], where [math]\displaystyle{ f^{-1}(y) = x }[/math] if and only if [math]\displaystyle{ f(x) = y }[/math], then the inverse function rule is, in Lagrange's notation,

[math]\displaystyle{ \left[f^{-1}\right]'(a)=\frac{1}{f'\left( f^{-1}(a) \right)} }[/math].

This formula holds in general whenever [math]\displaystyle{ f }[/math] is continuous and injective on an interval $I$ , with [math]\displaystyle{ f }[/math] being differentiable at [math]\displaystyle{ f^{-1}(a) }[/math]([math]\displaystyle{ \in I }[/math]) and where[math]\displaystyle{ f'(f^{-1}(a)) \ne 0 }[/math]. The same formula is also equivalent to the expression

[math]\displaystyle{ \mathcal{D}\left[f^{-1}\right]=\frac{1}{(\mathcal{D} f)\circ \left(f^{-1}\right)}, }[/math]

where [math]\displaystyle{ \mathcal{D} }[/math] denotes the unary derivative operator (on the space of functions) and [math]\displaystyle{ \circ }[/math] denotes function composition.

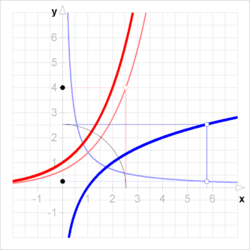
Geometrically, a function and inverse function have graphs that are reflections, in the line [math]\displaystyle{ y=x }[/math]. This reflection operation turns the gradient of any line into its reciprocal.^[1]

Assuming that [math]\displaystyle{ f }[/math] has an inverse in a neighbourhood of [math]\displaystyle{ x }[/math] and that its derivative at that point is non-zero, its inverse is guaranteed to be differentiable at [math]\displaystyle{ x }[/math] and have a derivative given by the above formula.

The inverse function rule may also be expressed in Leibniz's notation. As that notation suggests,

[math]\displaystyle{ \frac{dx}{dy}\,\cdot\, \frac{dy}{dx} = 1. }[/math]

This relation is obtained by differentiating the equation [math]\displaystyle{ f^{-1}(y)=x }[/math] in terms of $x$ and applying the chain rule, yielding that:

[math]\displaystyle{ \frac{dx}{dy}\,\cdot\, \frac{dy}{dx} = \frac{dx}{dx} }[/math]

considering that the derivative of $x$ with respect to $x$ is 1.

Derivation

Let [math]\displaystyle{ f }[/math] be an invertible (bijective) function, let [math]\displaystyle{ x }[/math] be in the domain of [math]\displaystyle{ f }[/math], and let [math]\displaystyle{ y }[/math] be in the codomain of [math]\displaystyle{ f }[/math]. Since f is a bijective function, [math]\displaystyle{ y }[/math] is in the range of [math]\displaystyle{ f }[/math]. This also means that [math]\displaystyle{ y }[/math] is in the domain of [math]\displaystyle{ f^{-1} }[/math], and that [math]\displaystyle{ x }[/math] is in the codomain of [math]\displaystyle{ f^{-1} }[/math]. Since [math]\displaystyle{ f }[/math] is an invertible function, we know that [math]\displaystyle{ f(f^{-1}(y)) = y }[/math]. The inverse function rule can be obtained by taking the derivative of this equation.

[math]\displaystyle{ \dfrac{\mathrm{d}}{\mathrm{d}y} f(f^{-1}(y)) = \dfrac{\mathrm{d}}{\mathrm{d}y} y }[/math]

The right side is equal to 1 and the chain rule can be applied to the left side:

[math]\displaystyle{ \begin{align} \dfrac{\mathrm{d}\left( f(f^{-1}(y)) \right)}{\mathrm{d}\left( f^{-1}(y) \right)} \dfrac{\mathrm{d}\left(f^{-1}(y)\right)}{\mathrm{d}y} &= 1 \\ \dfrac{\mathrm{d}f(f^{-1}(y))}{\mathrm{d}f^{-1}(y)} \dfrac{\mathrm{d}f^{-1}(y)}{\mathrm{d}y} &= 1 \\ f^{\prime}(f^{-1}(y)) (f^{-1})^{\prime}(y) &= 1 \end{align} }[/math]

Rearranging then gives

[math]\displaystyle{ (f^{-1})^{\prime}(y) = \frac{1}{f^{\prime}(f^{-1}(y))} }[/math]

Rather than using [math]\displaystyle{ y }[/math] as the variable, we can rewrite this equation using [math]\displaystyle{ a }[/math] as the input for [math]\displaystyle{ f^{-1} }[/math], and we get the following:^[2]

[math]\displaystyle{ (f^{-1})^{\prime}(a) = \frac{1}{f^{\prime}\left( f^{-1}(a) \right)} }[/math]

Examples

[math]\displaystyle{ y = x^2 }[/math] (for positive $x$ ) has inverse [math]\displaystyle{ x = \sqrt{y} }[/math].

[math]\displaystyle{ \frac{dy}{dx} = 2x \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \frac{dx}{dy} = \frac{1}{2\sqrt{y}}=\frac{1}{2x} }[/math]

[math]\displaystyle{ \frac{dy}{dx}\,\cdot\,\frac{dx}{dy} = 2x \cdot\frac{1}{2x} = 1. }[/math]

At [math]\displaystyle{ x=0 }[/math], however, there is a problem: the graph of the square root function becomes vertical, corresponding to a horizontal tangent for the square function.

[math]\displaystyle{ y = e^x }[/math] (for real $x$ ) has inverse [math]\displaystyle{ x = \ln{y} }[/math] (for positive [math]\displaystyle{ y }[/math])

[math]\displaystyle{ \frac{dy}{dx} = e^x \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \frac{dx}{dy} = \frac{1}{y} = e^{-x} }[/math]

[math]\displaystyle{ \frac{dy}{dx}\,\cdot\,\frac{dx}{dy} = e^x \cdot e^{-x} = 1. }[/math]

Additional properties

Integrating this relationship gives

[math]\displaystyle{ {f^{-1}}(x)=\int\frac{1}{f'({f^{-1}}(x))}\,{dx} + C. }[/math]

This is only useful if the integral exists. In particular we need [math]\displaystyle{ f'(x) }[/math] to be non-zero across the range of integration.

It follows that a function that has a continuous derivative has an inverse in a neighbourhood of every point where the derivative is non-zero. This need not be true if the derivative is not continuous.

Another very interesting and useful property is the following:

[math]\displaystyle{ \int f^{-1}(x)\, {dx} = x f^{-1}(x) - F(f^{-1}(x)) + C }[/math]

Where [math]\displaystyle{ F }[/math] denotes the antiderivative of [math]\displaystyle{ f }[/math].

The inverse of the derivative of f(x) is also of interest, as it is used in showing the convexity of the Legendre transform.

Let [math]\displaystyle{ z = f'(x) }[/math] then we have, assuming [math]\displaystyle{ f''(x) \neq 0 }[/math]:[math]\displaystyle{ \frac{d(f')^{-1}(z)}{dz} = \frac{1}{f''(x)} }[/math]This can be shown using the previous notation [math]\displaystyle{ y = f(x) }[/math]. Then we have:

[math]\displaystyle{ f'(x) = \frac{dy}{dx} = \frac{dy}{dz} \frac{dz}{dx} = \frac{dy}{dz} f''(x) \Rightarrow \frac{dy}{dz} = \frac{f'(x) }{f''(x)} }[/math]Therefore:

[math]\displaystyle{ \frac{d(f')^{-1}(z)}{dz} = \frac{dx}{dz} = \frac{dy}{dz}\frac{dx}{dy} = \frac{f'(x)}{f''(x)}\frac{1}{f'(x)} = \frac{1}{f''(x)} }[/math]

By induction, we can generalize this result for any integer [math]\displaystyle{ n \ge 1 }[/math], with [math]\displaystyle{ z = f^{(n)}(x) }[/math], the nth derivative of f(x), and [math]\displaystyle{ y = f^{(n-1)}(x) }[/math], assuming [math]\displaystyle{ f^{(i)}(x) \neq 0 \text{ for } 0 \lt i \le n+1 }[/math]:

[math]\displaystyle{ \frac{d(f^{(n)})^{-1}(z)}{dz} = \frac{1}{f^{(n+1)}(x)} }[/math]

Higher derivatives

The chain rule given above is obtained by differentiating the identity [math]\displaystyle{ f^{-1}(f(x))=x }[/math] with respect to $x$ . One can continue the same process for higher derivatives. Differentiating the identity twice with respect to $x$ , one obtains

[math]\displaystyle{ \frac{d^2y}{dx^2}\,\cdot\,\frac{dx}{dy} + \frac{d}{dx} \left(\frac{dx}{dy}\right)\,\cdot\,\left(\frac{dy}{dx}\right) = 0, }[/math]

that is simplified further by the chain rule as

[math]\displaystyle{ \frac{d^2y}{dx^2}\,\cdot\,\frac{dx}{dy} + \frac{d^2x}{dy^2}\,\cdot\,\left(\frac{dy}{dx}\right)^2 = 0. }[/math]

Replacing the first derivative, using the identity obtained earlier, we get

[math]\displaystyle{ \frac{d^2y}{dx^2} = - \frac{d^2x}{dy^2}\,\cdot\,\left(\frac{dy}{dx}\right)^3. }[/math]

Similarly for the third derivative:

[math]\displaystyle{ \frac{d^3y}{dx^3} = - \frac{d^3x}{dy^3}\,\cdot\,\left(\frac{dy}{dx}\right)^4 - 3 \frac{d^2x}{dy^2}\,\cdot\,\frac{d^2y}{dx^2}\,\cdot\,\left(\frac{dy}{dx}\right)^2 }[/math]

or using the formula for the second derivative,

[math]\displaystyle{ \frac{d^3y}{dx^3} = - \frac{d^3x}{dy^3}\,\cdot\,\left(\frac{dy}{dx}\right)^4 + 3 \left(\frac{d^2x}{dy^2}\right)^2\,\cdot\,\left(\frac{dy}{dx}\right)^5 }[/math]

These formulas are generalized by the Faà di Bruno's formula.

These formulas can also be written using Lagrange's notation. If $f$ and $g$ are inverses, then

[math]\displaystyle{ g''(x) = \frac{-f''(g(x))}{[f'(g(x))]^3} }[/math]

Example

[math]\displaystyle{ y = e^x }[/math] has the inverse [math]\displaystyle{ x = \ln y }[/math]. Using the formula for the second derivative of the inverse function,

[math]\displaystyle{ \frac{dy}{dx} = \frac{d^2y}{dx^2} = e^x = y \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \left(\frac{dy}{dx}\right)^3 = y^3; }[/math]

so that

[math]\displaystyle{ \frac{d^2x}{dy^2}\,\cdot\,y^3 + y = 0 \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \frac{d^2x}{dy^2} = -\frac{1}{y^2} }[/math],

which agrees with the direct calculation.

References

Marsden, Jerrold E.; Weinstein, Alan (1981). "Chapter 8: Inverse Functions and the Chain Rule". Calculus unlimited. Menlo Park, Calif.: Benjamin/Cummings Pub. Co. ISBN 0-8053-6932-5. https://authors.library.caltech.edu/25054/10/CalcUch8-invfunc-chainrule.pdf.

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Inverse function rule. Read more

[1] "Derivatives of Inverse Functions". https://oregonstate.edu/instruct/mth251/cq/Stage6/Lesson/inverseDeriv.html.

[2] "Derivatives of inverse functions". https://www.khanacademy.org/math/ap-calculus-ab/ab-differentiation-2-new/ab-3-3/v/derivatives-of-inverse-functions.

[1]

[2]

v t e Calculus
Precalculus	Binomial theorem Concave function Continuous function Factorial Finite difference Free variables and bound variables Fundamental theorem Graph of a function Linear function Mean value theorem Radian Rolle's theorem Secant Slope Tangent
Limits	Indeterminate form Limit of a function One-sided limit Limit of a sequence Orders of approximation (ε, δ)-definition of limit
Differential calculus	Chain rule Derivative Differential Differential equation Differential operator Implicit differentiation Inverse functions and differentiation L'Hôpital's rule Leibniz's rule Logarithmic derivative Mean value theorem Newton's method Notation Leibniz's notation Newton's notation Product rule Quotient rule Regiomontanus' angle maximization problem Related rates Simplest rules Constant factor rule in differentiation Linearity of differentiation Power rule Sum rule in differentiation Stationary point First derivative test Second derivative test Extreme value theorem Maxima and minima Taylor's theorem
Integral calculus	Antiderivative Arc length Constant of integration Differentiation under the integral sign Fundamental theorem of calculus Integral of secant cubed Integral of the secant function Integration by parts Integration by substitution Tangent half-angle substitution Partial fractions in integration Quadratic integral Proof that 22/7 exceeds π Simplest rules Constant factor rule in integration Linearity of integration Sum rule in integration Trapezoidal rule Trigonometric substitution
Vector calculus	Curl Directional derivative Divergence Divergence theorem Gradient Gradient theorem Green's theorem Laplacian Stokes' theorem
Multivariable calculus	Curvature Disc integration Divergence theorem Exterior Gabriel's Horn Geometric Hessian matrix Jacobian matrix and determinant Line integral Matrix Multiple integral Partial derivative Shell integration Surface integral Tensor Volume integral
Series	Abel's test Alternating Alternating series test Arithmetico-geometric sequence Binomial Cauchy condensation test Direct comparison test Dirichlet's test Euler–Maclaurin formula Fourier Geometric Harmonic Infinite Integral test for convergence Limit comparison test Maclaurin Power Ratio test Root test Taylor Term test
Special functions and numbers	Bernoulli numbers e (mathematical constant) Exponential function Natural logarithm Stirling's approximation
History of calculus	Adequality Brook Taylor Colin Maclaurin Generality of algebra Gottfried Wilhelm Leibniz Infinitesimal Infinitesimal calculus Isaac Newton Fluxion Law of Continuity Leonhard Euler Method of Fluxions The Method of Mechanical Theorems
Lists	Differentiation rules List of integrals of exponential functions List of integrals of hyperbolic functions List of integrals of inverse hyperbolic functions List of integrals of inverse trigonometric functions List of integrals of irrational functions List of integrals of logarithmic functions List of integrals of rational functions List of integrals of trigonometric functions List of limits List of mathematical symbols Lists of integrals

Anonymous

Search

Inverse function rule

Namespaces

More

Page actions

Contents

Derivation

Examples

Additional properties

Higher derivatives

Example

See also

References

Navigation

Navigation

Help

Translate

Wiki tools

Wiki tools

Anonymous

Search

Inverse function rule

Derivation

Examples

Additional properties

Higher derivatives

Example

See also

References

Navigation

Wiki tools

Page tools

Other projects

Categories