Khatri–Rao product
This article provides insufficient context for those unfamiliar with the subject. (January 2023) (Learn how and when to remove this template message) |
In mathematics, the Khatri–Rao product of matrices is defined as[1][2][3]
- [math]\displaystyle{ \mathbf{A} \ast \mathbf{B} = \left(\mathbf{A}_{ij} \otimes \mathbf{B}_{ij}\right)_{ij} }[/math]
in which the ij-th block is the mipi × njqj sized Kronecker product of the corresponding blocks of A and B, assuming the number of row and column partitions of both matrices is equal. The size of the product is then (Σi mipi) × (Σj njqj).
For example, if A and B both are 2 × 2 partitioned matrices e.g.:
- [math]\displaystyle{ \mathbf{A} = \left[ \begin{array} {c | c} \mathbf{A}_{11} & \mathbf{A}_{12} \\ \hline \mathbf{A}_{21} & \mathbf{A}_{22} \end{array} \right] = \left[ \begin{array} {c c | c} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \hline 7 & 8 & 9 \end{array} \right] ,\quad \mathbf{B} = \left[ \begin{array} {c | c} \mathbf{B}_{11} & \mathbf{B}_{12} \\ \hline \mathbf{B}_{21} & \mathbf{B}_{22} \end{array} \right] = \left[ \begin{array} {c | c c} 1 & 4 & 7 \\ \hline 2 & 5 & 8 \\ 3 & 6 & 9 \end{array} \right] , }[/math]
we obtain:
- [math]\displaystyle{ \mathbf{A} \ast \mathbf{B} = \left[ \begin{array} {c | c} \mathbf{A}_{11} \otimes \mathbf{B}_{11} & \mathbf{A}_{12} \otimes \mathbf{B}_{12} \\ \hline \mathbf{A}_{21} \otimes \mathbf{B}_{21} & \mathbf{A}_{22} \otimes \mathbf{B}_{22} \end{array} \right] = \left[ \begin{array} {c c | c c} 1 & 2 & 12 & 21 \\ 4 & 5 & 24 & 42 \\ \hline 14 & 16 & 45 & 72 \\ 21 & 24 & 54 & 81 \end{array} \right]. }[/math]
This is a submatrix of the Tracy–Singh product [4] of the two matrices (each partition in this example is a partition in a corner of the Tracy–Singh product) and also may be called the block Kronecker product.
Column-wise Kronecker product
A column-wise Kronecker product of two matrices may also be called the Khatri–Rao product. This product assumes the partitions of the matrices are their columns. In this case m1 = m, p1 = p, n = q and for each j: nj = pj = 1. The resulting product is a mp × n matrix of which each column is the Kronecker product of the corresponding columns of A and B. Using the matrices from the previous examples with the columns partitioned:
- [math]\displaystyle{ \mathbf{C} = \left[ \begin{array} { c | c | c} \mathbf{C}_1 & \mathbf{C}_2 & \mathbf{C}_3 \end{array} \right] = \left[ \begin{array} {c | c | c} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right] ,\quad \mathbf{D} = \left[ \begin{array} { c | c | c } \mathbf{D}_1 & \mathbf{D}_2 & \mathbf{D}_3 \end{array} \right] = \left[ \begin{array} { c | c | c } 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \end{array} \right] , }[/math]
so that:
- [math]\displaystyle{ \mathbf{C} \ast \mathbf{D} = \left[ \begin{array} { c | c | c } \mathbf{C}_1 \otimes \mathbf{D}_1 & \mathbf{C}_2 \otimes \mathbf{D}_2 & \mathbf{C}_3 \otimes \mathbf{D}_3 \end{array} \right] = \left[ \begin{array} { c | c | c } 1 & 8 & 21 \\ 2 & 10 & 24 \\ 3 & 12 & 27 \\ 4 & 20 & 42 \\ 8 & 25 & 48 \\ 12 & 30 & 54 \\ 7 & 32 & 63 \\ 14 & 40 & 72 \\ 21 & 48 & 81 \end{array} \right]. }[/math]
This column-wise version of the Khatri–Rao product is useful in linear algebra approaches to data analytical processing[5] and in optimizing the solution of inverse problems dealing with a diagonal matrix.[6][7]
In 1996 the Column-wise Khatri–Rao product was proposed to estimate the angles of arrival (AOAs) and delays of multipath signals[8] and four coordinates of signals sources[9] at a digital antenna array.
Face-splitting product
The alternative concept of the matrix product, which uses row-wise splitting of matrices with a given quantity of rows, was proposed by V. Slyusar[10] in 1996.[9][11][12][13][14]
This matrix operation was named the "face-splitting product" of matrices[11][13] or the "transposed Khatri–Rao product". This type of operation is based on row-by-row Kronecker products of two matrices. Using the matrices from the previous examples with the rows partitioned:
- [math]\displaystyle{ \mathbf{C} = \begin{bmatrix} \mathbf{C}_1 \\\hline \mathbf{C}_2 \\\hline \mathbf{C}_3\\ \end{bmatrix} = \begin{bmatrix} 1 & 2 & 3 \\\hline 4 & 5 & 6 \\\hline 7 & 8 & 9 \end{bmatrix} ,\quad \mathbf{D} = \begin{bmatrix} \mathbf{D}_1\\\hline \mathbf{D}_2\\\hline \mathbf{D}_3\\ \end{bmatrix} = \begin{bmatrix} 1 & 4 & 7 \\\hline 2 & 5 & 8 \\\hline 3 & 6 & 9 \end{bmatrix} , }[/math]
the result can be obtained:[9][11][13]
- [math]\displaystyle{ \mathbf{C} \bull \mathbf{D} = \begin{bmatrix} \mathbf{C}_1 \otimes \mathbf{D}_1\\\hline \mathbf{C}_2 \otimes \mathbf{D}_2\\\hline \mathbf{C}_3 \otimes \mathbf{D}_3\\ \end{bmatrix} = \begin{bmatrix} 1 & 4 & 7 & 2 & 8 & 14 & 3 & 12 & 21 \\\hline 8 & 20 & 32 & 10 & 25 & 40 & 12 & 30 & 48 \\\hline 21 & 42 & 63 & 24 & 48 & 72 & 27 & 54 & 81 \end{bmatrix}. }[/math]
Main properties
- Transpose (V. Slyusar, 1996[9][11][12]):
- [math]\displaystyle{ \left(\mathbf{A} \bull \mathbf{B}\right)^\textsf{T} = \textbf{A}^\textsf{T} \ast \mathbf{B}^\textsf{T} }[/math],
- Bilinearity and associativity:[9][11][12]
- [math]\displaystyle{ \begin{align} \mathbf{A} \bull (\mathbf{B} + \mathbf{C}) &= \mathbf{A} \bull \mathbf{B} + \mathbf{A} \bull \mathbf{C}, \\ (\mathbf{B} + \mathbf{C}) \bull \mathbf{A} &= \mathbf{B} \bull \mathbf{A} + \mathbf{C} \bull \mathbf{A}, \\ (k\mathbf{A}) \bull \mathbf{B} &= \mathbf{A} \bull (k\mathbf{B}) = k(\mathbf{A} \bull \mathbf{B}), \\ (\mathbf{A} \bull \mathbf{B}) \bull \mathbf{C} &= \mathbf{A} \bull (\mathbf{B} \bull \mathbf{C}), \\ \end{align} }[/math]
where A, B and C are matrices, and k is a scalar,
- [math]\displaystyle{ a \bull \mathbf{B} = \mathbf{B} \bull a }[/math],[12]
- The mixed-product property (V. Slyusar, 1997[12]):
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{B})\left(\mathbf{A}^\textsf{T} \ast \mathbf{B}^\textsf{T}\right) = \left(\mathbf{A}\mathbf{A}^\textsf{T}\right) \circ \left(\mathbf{B}\mathbf{B}^\textsf{T}\right) }[/math],
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{B})(\mathbf{C} \ast \mathbf{D}) = (\mathbf{A}\mathbf{C}) \circ (\mathbf{B} \mathbf{D}) }[/math],[13]
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{B} \bull \mathbf{C} \bull \mathbf{D})(\mathbf{L} \ast \mathbf{M} \ast \mathbf{N} \ast \mathbf{P}) = (\mathbf{A}\mathbf{L}) \circ (\mathbf{B} \mathbf{M}) \circ (\mathbf{C} \mathbf{N})\circ (\mathbf{D} \mathbf{P}) }[/math][15]
- [math]\displaystyle{ (\mathbf{A} \ast \mathbf{B})^\textsf{T}(\mathbf{A} \ast \mathbf{B}) = \left(\mathbf{A}^\textsf{T}\mathbf{A}\right) \circ \left(\mathbf{B}^\textsf{T} \mathbf{B}\right) }[/math],[16]
- [math]\displaystyle{ (\mathbf{A} \circ \mathbf{B}) \bull (\mathbf{C} \circ \mathbf{D}) = (\mathbf{A} \bull \mathbf{C}) \circ (\mathbf{B} \bull \mathbf{D}) }[/math],[12]
- [math]\displaystyle{ \mathbf{A} \otimes (\mathbf{B} \bull \mathbf{C}) = (\mathbf{A} \otimes \mathbf{B}) \bull \mathbf{C} }[/math],[9]
- [math]\displaystyle{ (\mathbf{A} \otimes \mathbf{B})(\mathbf{C} \ast \mathbf{D}) = (\mathbf{A}\mathbf{C}) \ast (\mathbf{B} \mathbf{D}) }[/math],[16]
- [math]\displaystyle{ (\mathbf{A} \otimes \mathbf{B}) \ast (\mathbf{C} \otimes \mathbf{D}) = \mathbf{P}[ (\mathbf{A} \ast \mathbf{C}) \otimes (\mathbf{B} \ast \mathbf{D})] }[/math], where [math]\displaystyle{ \mathbf{P} }[/math] is a permutation matrix.[7]
-
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{B})(\mathbf{C} \otimes \mathbf{D}) = (\mathbf{A}\mathbf{C}) \bull (\mathbf{B} \mathbf{D}) }[/math],[13][15]
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{L})(\mathbf{B} \otimes \mathbf{M}) \cdots (\mathbf{C} \otimes \mathbf{S}) = (\mathbf{A}\mathbf{B}\cdots\mathbf{C}) \bull (\mathbf{L}\mathbf{M}\cdots\mathbf{S}) }[/math],
-
- [math]\displaystyle{ c^\textsf{T} \bull d^\textsf{T} = c^\textsf{T} \otimes d^\textsf{T} }[/math],[12]
- [math]\displaystyle{ c \ast d = c \otimes d }[/math],
where [math]\displaystyle{ c }[/math] and [math]\displaystyle{ d }[/math] are vectors, - [math]\displaystyle{ \left(\mathbf{A} \ast c^\textsf{T}\right)d = \left(\mathbf{A} \ast d^\textsf{T}\right)c }[/math],[17] [math]\displaystyle{ d^\textsf{T}\left(c \bull \mathbf{A}^\textsf{T}\right) = c^\textsf{T}\left(d \bull \mathbf{A}^\textsf{T}\right) }[/math],
-
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{B})(c \otimes d) = (\mathbf{A}c) \circ (\mathbf{B}d) }[/math],[18]
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{B})(\mathbf{M}\mathbf{N}c \otimes \mathbf{Q}\mathbf{P}d) = (\mathbf{A}\mathbf{M}\mathbf{N}c) \circ (\mathbf{B}\mathbf{Q}\mathbf{P}d), }[/math]
-
- [math]\displaystyle{ \mathcal F\left(C^{(1)}x \star C^{(2)}y\right) = \left(\mathcal F C^{(1)} \bull \mathcal F C^{(2)}\right)(x \otimes y) = \mathcal F C^{(1)}x \circ \mathcal F C^{(2)}y }[/math],
where [math]\displaystyle{ \star }[/math] is vector convolution and [math]\displaystyle{ \mathcal F }[/math] is the Fourier transform matrix (this result is an evolving of count sketch properties[19]), -
- [math]\displaystyle{ \mathbf{A} \bull \mathbf{B} = \left(\mathbf {A} \otimes \mathbf {1_c}^\textsf{T}\right) \circ \left(\mathbf {1_k}^\textsf{T} \otimes \mathbf {B}\right) }[/math],[20]
- [math]\displaystyle{ \mathbf{M} \bull \mathbf{M} = \left(\mathbf{M} \otimes \mathbf{1}^\textsf{T}\right) \circ \left(\mathbf{1}^\textsf{T} \otimes \mathbf{M}\right) }[/math],[21]
- [math]\displaystyle{ \mathbf{M} \bull \mathbf{M} = \mathbf{M} [\circ] \left(\mathbf{M} \otimes \mathbf{1}^\textsf{T}\right) }[/math],
- [math]\displaystyle{ \mathbf{P} \ast \mathbf{N} = (\mathbf{P} \otimes \mathbf{1_c}) \circ (\mathbf {1_k} \otimes \mathbf {N}) }[/math], where [math]\displaystyle{ \mathbf {P} }[/math] is [math]\displaystyle{ c \times r }[/math] matrix, [math]\displaystyle{ \mathbf {N} }[/math] is [math]\displaystyle{ k \times r }[/math] matrix,.
-
- [math]\displaystyle{ \mathbf{W_d}\mathbf{A} = \mathbf{w} \bull \mathbf{A} }[/math],[12]
- [math]\displaystyle{ vec((\mathbf{w}^\textsf{T} \ast \mathbf{A})\mathbf{B})= (\mathbf{B}^\textsf{T} \ast \mathbf{A}) \mathbf{w} }[/math][13]= [math]\displaystyle{ vec(\mathbf{A}(\mathbf{w} \bull \mathbf{B})) }[/math],
- [math]\displaystyle{ \operatorname{vec}\left(\mathbf{A}^\textsf{T} \mathbf{W_d} \mathbf{A}\right) = \left(\mathbf{A} \bull \mathbf{A}\right)^\textsf{T} \mathbf{w} }[/math],[21]
where [math]\displaystyle{ \mathbf{w} }[/math] is the vector consisting of the diagonal elements of [math]\displaystyle{ \mathbf{W_d} }[/math], [math]\displaystyle{ \operatorname{vec}(\mathbf{A}) }[/math] means stack the columns of a matrix [math]\displaystyle{ \mathbf{A} }[/math] on top of each other to give a vector. -
- [math]\displaystyle{ (\mathbf{A} \bull \mathbf{L})(\mathbf{B} \otimes \mathbf{M}) \cdots (\mathbf{C} \otimes \mathbf{S})(\mathbf{K} \ast \mathbf{T}) = (\mathbf{A}\mathbf{B}...\mathbf{C}\mathbf{K}) \circ (\mathbf{L}\mathbf{M}...\mathbf{S}\mathbf{T}) }[/math].[13][15]
- [math]\displaystyle{ \begin{align} (\mathbf{A} \bull \mathbf{L})(\mathbf{B} \otimes \mathbf{M}) \cdots (\mathbf{C} \otimes \mathbf{S})(c \otimes d) &= (\mathbf{A}\mathbf{B} \cdots \mathbf{C}c) \circ (\mathbf{L}\mathbf{M} \cdots \mathbf{S}d), \\ (\mathbf{A} \bull \mathbf{L})(\mathbf{B} \otimes \mathbf{M}) \cdots (\mathbf{C} \otimes \mathbf{S})(\mathbf{P}c \otimes \mathbf{Q}d) &= (\mathbf{A}\mathbf{B} \cdots \mathbf{C}\mathbf{P}c) \circ (\mathbf{L}\mathbf{M}\cdots\mathbf{S}\mathbf{Q}d) \end{align} }[/math],
Examples[18]
- [math]\displaystyle{ \begin{align} &\left( \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \end{bmatrix} \bullet \begin{bmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} \right) \left( \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \otimes \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \right) \left( \begin{bmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \\ \end{bmatrix} \otimes \begin{bmatrix} \rho_1 & 0 \\ 0 & \rho_2 \\ \end{bmatrix} \right) \left( \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \ast \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} \right) \\[5pt] {}={} &\left( \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \end{bmatrix} \bullet \begin{bmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} \right) \left( \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \,\otimes\, \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} \rho_1 & 0 \\ 0 & \rho_2 \\ \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} \right) \\[5pt] {}={} & \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 \\ 0 & \sigma_2 \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \,\circ\, \begin{bmatrix} 1 & 0 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} \rho_1 & 0 \\ 0 & \rho_2 \\ \end{bmatrix} \begin{bmatrix} y_1 \\ y_2 \end{bmatrix} . \end{align} }[/math]
Theorem[18]
If [math]\displaystyle{ M = T^{(1)} \bullet \dots \bullet T^{(c)} }[/math], where [math]\displaystyle{ T^{(1)}, \dots, T^{(c)} }[/math] are independent components a random matrix [math]\displaystyle{ T }[/math] with independent identically distributed rows [math]\displaystyle{ T_1, \dots, T_m\in \mathbb R^d }[/math], such that
- [math]\displaystyle{ E\left[(T_1x)^2\right] = \left\|x\right\|_2^2 }[/math] and [math]\displaystyle{ E\left[(T_1 x)^p\right]^\frac{1}{p} \le \sqrt{ap}\|x\|_2 }[/math],
then for any vector [math]\displaystyle{ x }[/math]
- [math]\displaystyle{ \left| \left\|Mx\right\|_2 - \left\|x\right\|_2 \right| \lt \varepsilon \left\|x\right\|_2 }[/math]
with probability [math]\displaystyle{ 1 - \delta }[/math] if the quantity of rows
- [math]\displaystyle{ m = (4a)^{2c} \varepsilon^{-2} \log 1/\delta + (2ae)\varepsilon^{-1}(\log 1/\delta)^c. }[/math]
In particular, if the entries of [math]\displaystyle{ T }[/math] are [math]\displaystyle{ \pm 1 }[/math] can get
- [math]\displaystyle{ m = O\left(\varepsilon^{-2}\log1/\delta + \varepsilon^{-1}\left(\frac{1}{c}\log1/\delta\right)^c\right) }[/math]
which matches the Johnson–Lindenstrauss lemma of [math]\displaystyle{ m = O\left(\varepsilon^{-2}\log1/\delta\right) }[/math] when [math]\displaystyle{ \varepsilon }[/math] is small.
Block face-splitting product
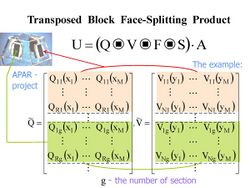
According to the definition of V. Slyusar[9][13] the block face-splitting product of two partitioned matrices with a given quantity of rows in blocks
- [math]\displaystyle{ \mathbf{A} = \left[ \begin{array} {c | c} \mathbf{A}_{11} & \mathbf{A}_{12} \\ \hline \mathbf{A}_{21} & \mathbf{A}_{22} \end{array} \right] ,\quad \mathbf{B} = \left[ \begin{array} {c | c} \mathbf{B}_{11} & \mathbf{B}_{12} \\ \hline \mathbf{B}_{21} & \mathbf{B}_{22} \end{array} \right] , }[/math]
can be written as :
- [math]\displaystyle{ \mathbf{A} [\bull] \mathbf{B} = \left[ \begin{array} {c | c} \mathbf{A}_{11} \bull \mathbf{B}_{11} & \mathbf{A}_{12} \bull \mathbf{B}_{12} \\ \hline \mathbf{A}_{21} \bull \mathbf{B}_{21} & \mathbf{A}_{22} \bull \mathbf{B}_{22} \end{array} \right] . }[/math]
The transposed block face-splitting product (or Block column-wise version of the Khatri–Rao product) of two partitioned matrices with a given quantity of columns in blocks has a view:[9][13]
- [math]\displaystyle{ \mathbf{A} [\ast] \mathbf{B} = \left[ \begin{array} {c | c} \mathbf{A}_{11} \ast \mathbf{B}_{11} & \mathbf{A}_{12} \ast \mathbf{B}_{12} \\ \hline \mathbf{A}_{21} \ast \mathbf{B}_{21} & \mathbf{A}_{22} \ast \mathbf{B}_{22} \end{array} \right]. }[/math]
Main properties
- Transpose:
- [math]\displaystyle{ \left(\mathbf{A} [\ast] \mathbf{B} \right)^\textsf{T} = \textbf{A}^\textsf{T} [\bull] \mathbf{B}^\textsf{T} }[/math][15]
Applications
The Face-splitting product and the Block Face-splitting product used in the tensor-matrix theory of digital antenna arrays. These operations used also in:
- Artificial Intelligence and Machine learning systems to minimization of convolution and tensor sketch operations,[18]
- A popular Natural Language Processing models, and hypergraph models of similarity,[22]
- Generalized linear array model in statistics[21]
- Two- and multidimensional P-spline approximation of data,[20]
- Studies of genotype x environment interactions.[23]
See also
Notes
- ↑ Khatri C. G., C. R. Rao (1968). "Solutions to some functional equations and their applications to characterization of probability distributions". Sankhya 30: 167–180. http://library.isical.ac.in:8080/xmlui/bitstream/handle/10263/614/68.E02.pdf. Retrieved 2008-08-21.
- ↑ Liu, Shuangzhe (1999). "Matrix Results on the Khatri–Rao and Tracy–Singh Products". Linear Algebra and Its Applications 289 (1–3): 267–277. doi:10.1016/S0024-3795(98)10209-4.
- ↑ Zhang X; Yang Z; Cao C. (2002), "Inequalities involving Khatri–Rao products of positive semi-definite matrices", Applied Mathematics E-notes 2: 117–124
- ↑ Liu, Shuangzhe; Trenkler, Götz (2008). "Hadamard, Khatri-Rao, Kronecker and other matrix products". International Journal of Information and Systems Sciences 4 (1): 160–177.
- ↑ See e.g. H. D. Macedo and J.N. Oliveira. A linear algebra approach to OLAP. Formal Aspects of Computing, 27(2):283–307, 2015.
- ↑ Lev-Ari, Hanoch (2005-01-01). "Efficient Solution of Linear Matrix Equations with Application to Multistatic Antenna Array Processing" (in EN). Communications in Information & Systems 05 (1): 123–130. doi:10.4310/CIS.2005.v5.n1.a5. ISSN 1526-7555. http://www.ims.cuhk.edu.hk/~cis/2005.1/05.pdf.
- ↑ 7.0 7.1 Masiero, B.; Nascimento, V. H. (2017-05-01). "Revisiting the Kronecker Array Transform". IEEE Signal Processing Letters 24 (5): 525–529. doi:10.1109/LSP.2017.2674969. ISSN 1070-9908. Bibcode: 2017ISPL...24..525M. https://zenodo.org/record/896497.
- ↑ Vanderveen, M. C., Ng, B. C., Papadias, C. B., & Paulraj, A. (n.d.). Joint angle and delay estimation (JADE) for signals in multipath environments. Conference Record of The Thirtieth Asilomar Conference on Signals, Systems and Computers. – DOI:10.1109/acssc.1996.599145
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 Slyusar, V. I. (December 27, 1996). "End products in matrices in radar applications.". Radioelectronics and Communications Systems 41 (3): 50–53. http://slyusar.kiev.ua/en/IZV_1998_3.pdf.
- ↑ Anna Esteve, Eva Boj & Josep Fortiana (2009): "Interaction Terms in Distance-Based Regression," Communications in Statistics – Theory and Methods, 38:19, p. 3501 [1]
- ↑ 11.0 11.1 11.2 11.3 11.4 Slyusar, V. I. (1997-05-20). "Analytical model of the digital antenna array on a basis of face-splitting matrix products.". Proc. ICATT-97, Kyiv: 108–109. http://slyusar.kiev.ua/ICATT97.pdf.
- ↑ 12.0 12.1 12.2 12.3 12.4 12.5 12.6 12.7 Slyusar, V. I. (1997-09-15). "New operations of matrices product for applications of radars". Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73–74. http://slyusar.kiev.ua/DIPED_1997.pdf.
- ↑ 13.0 13.1 13.2 13.3 13.4 13.5 13.6 13.7 13.8 13.9 Slyusar, V. I. (March 13, 1998). "A Family of Face Products of Matrices and its Properties". Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz. 1999. 35 (3): 379–384. doi:10.1007/BF02733426. http://slyusar.kiev.ua/FACE.pdf.
- ↑ Slyusar, V. I. (2003). "Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels". Radioelectronics and Communications Systems 46 (10): 9–17. http://slyusar.kiev.ua/en/IZV_2003_10.pdf.
- ↑ 15.0 15.1 15.2 15.3 15.4 Vadym Slyusar. New Matrix Operations for DSP (Lecture). April 1999. – DOI: 10.13140/RG.2.2.31620.76164/1
- ↑ 16.0 16.1 C. Radhakrishna Rao. Estimation of Heteroscedastic Variances in Linear Models.//Journal of the American Statistical Association, Vol. 65, No. 329 (Mar., 1970), pp. 161–172
- ↑ Kasiviswanathan, Shiva Prasad, et al. «The price of privately releasing contingency tables and the spectra of random matrices with correlated rows.» Proceedings of the forty-second ACM symposium on Theory of computing. 2010.
- ↑ 18.0 18.1 18.2 18.3 Thomas D. Ahle, Jakob Bæk Tejs Knudsen. Almost Optimal Tensor Sketch. Published 2019. Mathematics, Computer Science, ArXiv
- ↑ Ninh, Pham (2013). "Fast and scalable polynomial kernels via explicit feature maps". SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. doi:10.1145/2487575.2487591.
- ↑ 20.0 20.1 Eilers, Paul H.C.; Marx, Brian D. (2003). "Multivariate calibration with temperature interaction using two-dimensional penalized signal regression.". Chemometrics and Intelligent Laboratory Systems 66 (2): 159–174. doi:10.1016/S0169-7439(03)00029-7.
- ↑ 21.0 21.1 21.2 Currie, I. D.; Durban, M.; Eilers, P. H. C. (2006). "Generalized linear array models with applications to multidimensional smoothing". Journal of the Royal Statistical Society 68 (2): 259–280. doi:10.1111/j.1467-9868.2006.00543.x.
- ↑ Bryan Bischof. Higher order co-occurrence tensors for hypergraphs via face-splitting. Published 15 February 2020, Mathematics, Computer Science, ArXiv
- ↑ Johannes W. R. Martini, Jose Crossa, Fernando H. Toledo, Jaime Cuevas. On Hadamard and Kronecker products in covariance structures for genotype x environment interaction.//Plant Genome. 2020;13:e20033. Page 5. [2]
References
- Khatri C. G., C. R. Rao (1968). "Solutions to some functional equations and their applications to characterization of probability distributions". Sankhya 30: 167–180. http://sankhya.isical.ac.in/search/30a2/30a2019.html. Retrieved 2008-08-21.
- Rao C.R.; Rao M. Bhaskara (1998), Matrix Algebra and Its Applications to Statistics and Econometrics, World Scientific, pp. 216
- Zhang X; Yang Z; Cao C. (2002), "Inequalities involving Khatri–Rao products of positive semi-definite matrices", Applied Mathematics E-notes 2: 117–124
- Liu Shuangzhe; Trenkler Götz (2008), "Hadamard, Khatri-Rao, Kronecker and other matrix products", International Journal of Information and Systems Sciences 4: 160–177
 |



