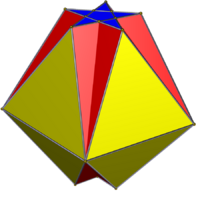
Rectified antiprism
| Set of rectified antiprisms | |
|---|---|
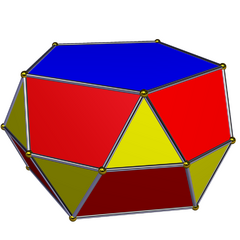 Rectified pentagonal antiprism | |
| Conway polyhedron notation | aAn |
| Faces | 2 n-gons 2n trapezoids 2n triangles |
| Edges | 8n |
| Vertices | 4n |
| Symmetry group | Dnd, [2+,2n], (2*n), order 4n |
| Rotation group | Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron | Elongated trapezohedron |
| Properties | convex |
In geometry, a rectified antiprism (also rectified bipyramid) is one of an infinite set of polyhedra, constructed as a rectification of an n-gonal antiprism, truncating the vertices down to the midpoint of the original edges. In Conway polyhedron notation, it is represented as aAn, an ambo-antiprism. The lateral squares or rectangular faces of the antiprism become squares or rhombic faces, and new isosceles triangle faces are truncations of the original vertices. It can also be seen as two base-to-base cupola as gyrobicupolae
Elements
An n-gonal form has 3n vertices, 7n edges, and 3n faces: 2 regular n-gons, 2n trapezohedron, and 2n triangles.
Forms
The rectified triangular antiprism is the same as a semiregular cuboctahedron.
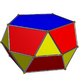
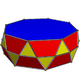
| n | 2 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | n |
|---|---|---|---|---|---|---|---|---|---|
| Image | 
|

|
|

|
|
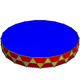
|
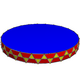
| ||
| Net | 
|

|

|
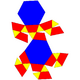
|

|
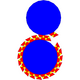
|

| ||
| Faces | 4 triangles 4 squares |
2 triangle 6 triangles 6 squares |
2 squares 8 triangles 8 squares |
2 pentagons 10 triangles 10 squares |
2 hexagons 12 triangles 12 squares |
2 octagons 16 triangles 16 squares |
2 decagons 20 triangles 20 squares |
2 dodecagons 24 triangles 24 squares |
2 n-gons 2n triangles 2n squares |
| Edges | 16-2=14 | 24 | 32 | 40 | 48 | 64 | 80 | 96 | 8n |
| Vertices | 8 | 12 | 16 | 20 | 24 | 32 | 40 | 48 | 4n |
| Related | 
|

|

|

|

|

|

|

|

|
| Net | 
|

|

|

|

|
|
|
| |
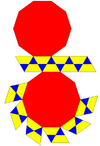
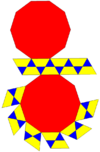
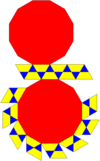
| Related |  Gyrobifastigium |
 Cuboctahedron |
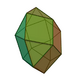 Square gyrobicupola |
Pentagonal gyrobicupola |
Star forms
Rectified star antiprisms also exist, like 5/2 and 5/3 forms:
Dual
| Set of joined antiprisms | |
|---|---|

| |
| Conway polyhedron notation | jAn |
| Faces | 4n |
| Edges | 8n |
| Vertices | 2+4n |
| Symmetry group | Dnd, [2+,2n], (2*n), order 4n |
| Rotation group | Dn, [2,n]+, (22n), order 2n |
| Dual polyhedron | Rectified antiprism Rectified bipyramid |
| Properties | convex |
The dual of a rectified antiprism is an elongated trapezohedron. The degenerate n=2 case, is an elongated tetragonal disphenoid, with the polar axis vertices removed. It can also be constructed as a joined antiprism in Conway polyhedron notation. The elongated triangular antiprism is a rhombic dodecahedron. The topology also exists on a 2n-gonal prism with the top and bottom faces divided with alternate orientations top to bottom.
| n | 2 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | n |
|---|---|---|---|---|---|---|---|---|---|
| Image | 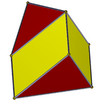
|

|

|

|

|

|

|

| |
| Net | 
|

|
|
|

|

|

|

| |
| Faces | 8 | 12 | 16 | 20 | 24 | 32 | 40 | 48 | 4n |
| Edges | 16-2=14 | 24 | 32 | 40 | 48 | 64 | 80 | 96 | 8n |
| Vertices | 10-2=8 | 14 | 18 | 22 | 26 | 34 | 42 | 50 | 2+4n |
| Related | 
|
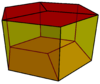
|
|
See also
External links
- Conway Notation for Polyhedra Try: aAn and jAn, where n=3,4,5,6... example aA3 is a rectified triangular antiprism, and jA3 is an joined triangular antiprism or a elongated triangular trapezohedron.