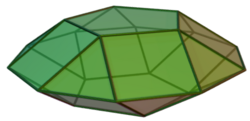
Pentagonal gyrobicupola

Short description: 31st Johnson solid (22 faces)

Pentagonal gyrobicupola
Type	Bicupola, Johnson J30 – J31 – J32
Faces	10 triangles 10 squares 2 pentagons
Edges	40
Vertices	20
Vertex configuration	$10\times (3\times 4\times 3\times 4)$ $10\times (3\times 4\times 5\times 4)$
Symmetry group	$D_{5\mathrm{d}}$
Properties	convex, composite
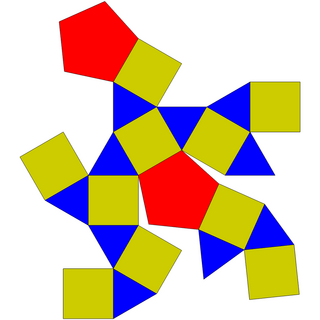
Net

The pentagonal gyrobicupola is a polyhedron that is constructed by attaching two pentagonal cupolas base-to-base, each of its cupolas is twisted at 36°. It is an example of a Johnson solid and a composite polyhedron.

Construction

The pentagonal gyrobicupola is a composite polyhedron: it is constructed by attaching two pentagonal cupolas base-to-base. This construction is similar to the pentagonal orthobicupola; the difference is that one of the cupolas in the pentagonal gyrobicupola is twisted at 36°, as suggested by the prefix gyro-. The resulting polyhedron has the same faces as the pentagonal orthobicupola does: those cupolas cover their decagonal bases, replacing them with ten equilateral triangles, ten squares, and two regular pentagons. A convex polyhedron in which all of its faces are regular polygons is the Johnson solid. The pentagonal gyrobicupola has these, enumerating it as the thirty-first Johnson solid $J_{31}$.

Properties

File:J31 pentagonal gyrobicupola.stl The surface area of a pentagonal gyrobicupola $A$ is the sum of its faces' area, and its volume $V$ is twice the volume of a pentagonal cupola: $$\begin{array}{rl}A& =\frac{20+\sqrt{100+10\sqrt{5}+10\sqrt{75+30\sqrt{5}}}}{2}{a}^2\approx 17.771a^2,\\ V& =\frac{5+4\sqrt{5}}{3}{a}^3\approx 4.648a^3.\end{array}$$

The dihedral angles of a pentagonal gyrobicupola are as follows:

• the angle between a pentagon and a square is 159.09°.
• the angle between a square and a triangle, within one cupola, is 148.28°;
• the dihedral angle at the plane joining the two cupolas is the sum of the dihedral angle between square-to-decagon and triangle-to-decagon, 69.09°.

External links

• Eric W. Weisstein, Pentagonal gyrobicupola (Johnson solid) at MathWorld.