1 33 honeycomb

133 honeycomb
(no image)
Type	Uniform tessellation
Schläfli symbol	{3,33,3}
Coxeter symbol	133
Coxeter-Dynkin diagram	or
7-face type	132 30px
6-face types	12230px 13130px
5-face types	12125px {34}25px
4-face type	11125px {33}25px
Cell type	10125px
Face type	{3}25px
Cell figure	Square
Face figure	Triangular duoprism 25px
Edge figure	Tetrahedral duoprism
Vertex figure	Trirectified 7-simplex 25px
Coxeter group	${\tilde{E}}_7$, 3,33,3
Properties	vertex-transitive, facet-transitive

In 7-dimensional geometry, 1₃₃ is a uniform honeycomb, also given by Schläfli symbol {3,3^3,3}, and is composed of 1₃₂ facets.

Construction

It is created by a Wythoff construction upon a set of 8 hyperplane mirrors in 7-dimensional space.

The facet information can be extracted from its Coxeter-Dynkin diagram.

Removing a node on the end of one of the 3-length branch leaves the 1₃₂, its only facet type.

The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the trirectified 7-simplex, 0₃₃.

The edge figure is determined by removing the ringed nodes of the vertex figure and ringing the neighboring node. This makes the tetrahedral duoprism, {3,3}×{3,3}.

Kissing number

Each vertex of this polytope corresponds to the center of a 6-sphere in a moderately dense sphere packing, in which each sphere is tangent to 70 others; the best known for 7 dimensions (the kissing number) is 126.

Geometric folding

The ${\tilde{E}}_7$ group is related to the ${\tilde{F}}_4$ by a geometric folding, so this honeycomb can be projected into the 4-dimensional demitesseractic honeycomb.

${\tilde{E}}_7$	${\tilde{F}}_4$
{3,33,3}	{3,3,4,3}

E₇^* lattice

${\tilde{E}}_7$ contains ${\tilde{A}}_7$ as a subgroup of index 144. Both ${\tilde{E}}_7$ and ${\tilde{A}}_7$ can be seen as affine extension from $A_7$ from different nodes: File:Affine A7 E7 relations.png

The E₇^* lattice (also called E₇²) has double the symmetry, represented by 3,3^3,3. The Voronoi cell of the E₇^* lattice is the 1₃₂ polytope, and voronoi tessellation the 1₃₃ honeycomb. The E₇^* lattice is constructed by 2 copies of the E₇ lattice vertices, one from each long branch of the Coxeter diagram, and can be constructed as the union of four A₇^* lattices, also called A₇⁴:

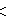
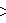
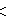
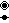
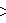
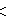
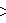
∪ = ∪ ∪ ∪ = dual of .

Related polytopes and honeycombs

The 1₃₃ is fourth in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 1_3k series. The final is a noncompact hyperbolic honeycomb, 1₃₄. Template:1 3k polytopes

Rectified 1₃₃ honeycomb

Rectified 133 honeycomb
(no image)
Type	Uniform tessellation
Schläfli symbol	{33,3,1}
Coxeter symbol	0331
Coxeter-Dynkin diagram	or
7-face type	Trirectified 7-simplex Rectified 1 32
6-face types	Birectified 6-simplex Birectified 6-cube Rectified 1 22
5-face types	Rectified 5-simplex Birectified 5-simplex Birectified 5-orthoplex
4-face type	5-cell Rectified 5-cell 24-cell
Cell type	{3,3} {3,4}
Face type	{3}
Vertex figure	{}×{3,3}×{3,3}
Coxeter group	${\tilde{E}}_7$, 3,33,3
Properties	vertex-transitive, facet-transitive

The rectified 1₃₃ or 0₃₃₁, Coxeter diagram has facets and , and vertex figure .

See also

• 8-polytope
• 3₃₁ honeycomb

References

• H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Coxeter The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN 978-0-486-40919-1 (Chapter 3: Wythoff's Construction for Uniform Polytopes)
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
• Klitzing, Richard. "7D Heptacombs o3o3o3o3o3o3o *d3x - linoh". https://bendwavy.org/klitzing/dimensions/flat.htm#7D. 
• Klitzing, Richard. "7D Heptacombs o3o3o3x3o3o3o *d3o - rolinoh". https://bendwavy.org/klitzing/dimensions/flat.htm#7D. 

Fundamental convex regular and uniform honeycombs in dimensions 2-9
Space	Family	${\tilde{A}}_{n-1}$	${\tilde{C}}_{n-1}$	${\tilde{B}}_{n-1}$	${\tilde{D}}_{n-1}$	${\tilde{G}}_2$ / ${\tilde{F}}_4$ / ${\tilde{E}}_{n-1}$
E2	Uniform tiling	{3[3]}	δ3	hδ3	qδ3	Hexagonal
E3	Uniform convex honeycomb	{3[4]}	δ4	hδ4	qδ4
E4	Uniform 4-honeycomb	{3[5]}	δ5	hδ5	qδ5	24-cell honeycomb
E5	Uniform 5-honeycomb	{3[6]}	δ6	hδ6	qδ6
E6	Uniform 6-honeycomb	{3[7]}	δ7	hδ7	qδ7	222
E7	Uniform 7-honeycomb	{3[8]}	δ8	hδ8	qδ8	133 • 331
E8	Uniform 8-honeycomb	{3[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E9	Uniform 9-honeycomb	{3[10]}	δ10	hδ10	qδ10
En-1	Uniform (n-1)-honeycomb	{3[n]}	δn	hδn	qδn	1k2 • 2k1 • k21