Bilunabirotunda

From HandWiki

In geometry, the bilunabirotunda is a Johnson solid with faces of 8 equilateral triangles, 2 squares, and 4 regular pentagons.

Properties

The bilunabirotunda is named from the prefix lune, meaning a figure featuring two triangles adjacent to opposite sides of a square. Therefore, the faces of a bilunabirotunda possess 8 equilateral triangles, 2 squares, and 4 regular pentagons as it faces.[1] It is one of the Johnson solids—a convex polyhedron in which all of the faces are regular polygon—enumerated as 91st Johnson solid J91.[2]

The surface area of a bilunabirotunda with edge length a is:[1] (2+23+5(5+25))a2≈12.346a2, and the volume of a bilunabirotunda is:[1] 17+9512a3≈3.0937a3.

Construction

The bilunabirotunda is an elementary polyhedron: it cannot be separated by a plane into two small regular-faced polyhedra.[3] One way to construct a bilunabirotunda is by attaching two wedges and two tridiminished icosahedrons.[4]

For edge length 5−1 is by union of the orbits of the coordinates, the bilunabirotunda is: (0,0,1),(5−12,1,5−12),(5+12,5−12,0). under the group action (of order 8) generated by reflections about coordinate planes.[5]

Applications

(Reynolds 2004) discusses the bilunabirotunda as a shape that could be used in architecture.[6]

Six bilunabirotundae around a cube

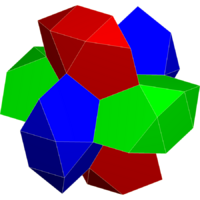
Six bilunabirotundae can be augmented around a cube with pyritohedral symmetry. B. M. Stewart labeled this six-bilunabirotunda model as 6J91(P4).[7] Such clusters combine with regular dodecahedra to form a space-filling honeycomb.

References

  1. ↑ 1.0 1.1 1.2 Berman, M. (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. 
  2. ↑ Francis, D. (August 2013). "Johnson solids & their acronyms". Word Ways 46 (3): 177. https://go.gale.com/ps/i.do?id=GALE%7CA340298118. 
  3. ↑ Cromwell, P. R. (1997). Polyhedra. Cambridge University Press. p. 86–87, 89. ISBN 978-0-521-66405-9. https://archive.org/details/polyhedra0000crom/page/87/mode/1up. 
  4. ↑ Gailiunas, Paul (2001). "Bridges: Mathematical Connections in Art, Music, and Science". doi:10.1007/s00004-001-0036-3. 
  5. ↑ Timofeenko, A. V. (2009). "The Non-Platonic and Non-Archimedean Noncomposite Polyhedra". Journal of Mathematical Sciences 162 (5): 710–729. doi:10.1007/s10958-009-9655-0. 
  6. ↑ Reynolds, M. A. (2004). "The Bilunabirotunda". Nexus Network Journal 6: 43–47. doi:10.1007/s00004-004-0005-8. 
  7. ↑ B. M. Stewart, Adventures Among the Toroids: A Study of Quasi-Convex, Aplanar, Tunneled Orientable Polyhedra of Positive Genus Having Regular Faces With Disjoint Interiors (1980) ISBN 978-0686119364, (page 127, 2nd ed.) polyhedron 6J91(P4).



Retrieved from "https://handwiki.org/wiki/index.php?title=Bilunabirotunda&oldid=4155026"