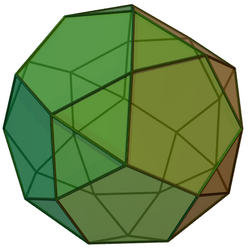
Pentagonal orthobirotunda

Short description: 34th Johnson solid (32 faces)

Pentagonal orthobirotunda
Type	Birotunda, Johnson J33 – J34 – J35
Faces	2×10 triangles 2+10 pentagons
Edges	60
Vertices	30
Vertex configuration	10(32.52) 2.10(3.5.3.5)
Symmetry group	D5h
Properties	convex
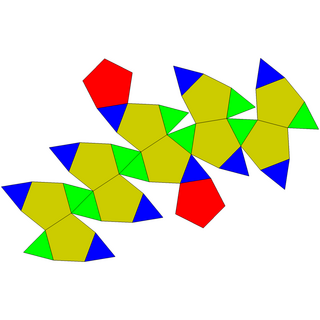
Net

In geometry, the pentagonal orthobirotunda is a polyhedron constructed by attaching two pentagonal rotundae along their decagonal faces, matching like faces. It is a Johnson solid.

Construction

The pentagonal orthobirotunda is constructed by attaching two pentagonal rotundas to their base, covering decagon faces. The resulting polyhedron has 32 faces, 30 vertices, and 60 edges. This construction is similar to icosidodecahedron (or pentagonal gyrobirotunda), an Archimedean solid: the difference is one of its rotundas twisted around 36°, making the pentagonal faces connect to the triangular one, a process known as gyration. A convex polyhedron in which all of the faces are regular polygons is the Johnson solid. The pentagonal orthobirotunda is one of them, enumerated as the 34th Johnson solid $J_{34}$.

The difference between icosidodecahedron and pentagonal orthobirotunda, and its dissection.

Properties

The surface area of an icosidodecahedron $A$ can be determined by calculating the area of all pentagonal faces. The volume of an icosidodecahedron $V$ can be determined by slicing it into two pentagonal rotundae, after which summing up their volumes. Therefore, its surface area and volume can be formulated as: $$\begin{array}{rlr}A& =(5\sqrt{3}+3\sqrt{25+10\sqrt{5}})a^2& \approx 29.306a^2\\ V& =\frac{45+17\sqrt{5}}{6}{a}^3& \approx 13.836a^3.\end{array}$$

External links

• Eric W. Weisstein, Pentagonal orthobirotunda (Johnson solid) at MathWorld.