Pentagonal rotunda

Short description: 6th Johnson solid (17 faces)

Pentagonal rotunda
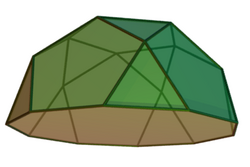Type	Johnson J5 – J6 – J7
Faces	10 triangles 1+5 pentagons 1 decagon
Edges	35
Vertices	20
Vertex configuration	2.5(3.5.3.5) 10(3.5.10)
Symmetry group	C5v
Rotation group	C5, [5]+, (55)
Dual polyhedron	-
Properties	convex
Net

In geometry, the pentagonal rotunda is one of the Johnson solids (J₆). It can be seen as half of an icosidodecahedron, or as half of a pentagonal orthobirotunda. It has a total of 17 faces.

A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.

Formulae

The following formulae for volume, surface area, circumradius, and height are valid if all faces are regular, with edge length a:

[math]\displaystyle{ V=\left(\frac{1}{12}\left(45+17\sqrt{5}\right)\right)a^3\approx6.91776...a^3 }[/math]

[math]\displaystyle{ \begin{align} A&=\left(\frac{1}{2}\sqrt{5\left(145+58\sqrt{5}+2\sqrt{30\left(65+29\sqrt{5}\right)}\right)}\right)a^2 \\ &=\left(\frac{1}{2}\left(5\sqrt{3}+\sqrt{10\left(65+29\sqrt{5}\right)}\right)\right)a^2\approx22.3472...a^2 \end{align} }[/math]

[math]\displaystyle{ R=\left(\frac{1}{2}\left(1+\sqrt{5}\right)\right)a\approx1.61803...a }[/math]

[math]\displaystyle{ H=\left(\sqrt{1+\frac{2}{\sqrt{5}}}\right)a\approx1.37638...a }[/math]

Dual polyhedron

The dual of the pentagonal rotunda has 20 faces: 10 triangular, 5 rhombic, and 5 kites.

Dual pentagonal rotunda	Net of dual

External links

• Eric W. Weisstein, Pentagonal rotunda (Johnson solid) at MathWorld.