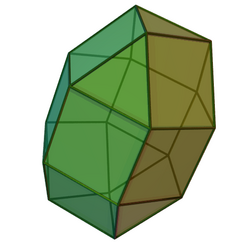
Elongated triangular gyrobicupola

Short description: 36th Johnson solid (20 faces)

Elongated triangular gyrobicupola
Type	Johnson J35 – J36 – J37
Faces	8 triangles 12 squares
Edges	36
Vertices	18
Vertex configuration	$\begin{array}{rl}& 6\times (3\times 4\times 3\times 4)+\\ & 12\times (3\times 4^3)\end{array}$
Symmetry group	$D_{3h}$
Properties	convex
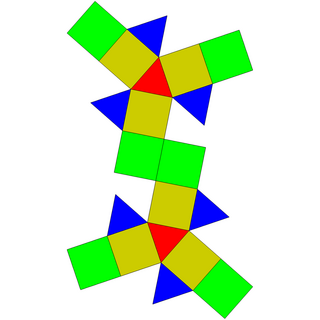
Net

In geometry, the elongated triangular gyrobicupola is a polyhedron constructed by attaching two regular triangular cupolas to the base of a regular hexagonal prism, with one of them rotated in $60^{\circ }$. It is an example of Johnson solid. File:J36 elongated triangular gyrobicupola.stl

Construction

The elongated triangular gyrobicupola is similarly can be constructed as the elongated triangular orthobicupola, started from a hexagonal prism by attaching two regular triangular cupolae onto its base, covering its hexagonal faces. This construction process is known as elongation, giving the resulting polyhedron has 8 equilateral triangles and 12 squares. The difference between those two polyhedrons is one of two triangular cupolas in the elongated triangular gyrobicupola is rotated in $60^{\circ }$. A convex polyhedron in which all faces are regular is Johnson solid, and the elongated triangular gyrobicupola is one among them, enumerated as 36th Johnson solid $J_{36}$.

Properties

An elongated triangular gyrobicupola with a given edge length $a$ has a surface area by adding the area of all regular faces: $$(12+2\sqrt{3})a^2\approx 15.464a^2.$$ Its volume can be calculated by cutting it off into two triangular cupolae and a hexagonal prism with regular faces, and then adding their volumes up: $$(\frac{5\sqrt{2}}{3}+\frac{3\sqrt{3}}{2})a^3\approx 4.955a^3.$$

Its three-dimensional symmetry groups is the prismatic symmetry, the dihedral group $D_{3d}$ of order 12. Its dihedral angle can be calculated by adding the angle of the triangular cupola and hexagonal prism. The dihedral angle of a hexagonal prism between two adjacent squares is the internal angle of a regular hexagon $120^{\circ }=2\pi /3$, and that between its base and square face is $\pi /2=90^{\circ }$. The dihedral angle of a regular triangular cupola between each triangle and the hexagon is approximately $70.5^{\circ }$, that between each square and the hexagon is $54.7^{\circ }$, and that between square and triangle is $125.3^{\circ }$. The dihedral angle of an elongated triangular orthobicupola between the triangle-to-square and square-to-square, on the edge where the triangular cupola and the prism is attached, is respectively: $$\begin{array}{rl}\frac{\pi }{2}+70.5^{\circ }& \approx 160.5^{\circ },\\ \frac{\pi }{2}+54.7^{\circ }& \approx 144.7^{\circ }.\end{array}$$

Related polyhedra and honeycombs

The elongated triangular gyrobicupola forms space-filling honeycombs with tetrahedra and square pyramids.

External links

• Eric W. Weisstein, Elongated triangular gyrobicupola (Johnson solid) at MathWorld.