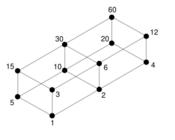
Square-free integer

Short description: Number without repeated prime factors

10 is square-free, as its divisors greater than 1 are 2, 5, and 10, none of which is square (the first few squares being 1, 4, 9, and 16)

Square-free integers up to 120 remain after eliminating multiples of squares of primes up to √120

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 3². The smallest positive square-free numbers are

1, 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21, 22, 23, 26, 29, 30, 31, 33, 34, 35, 37, 38, 39, ... (sequence A005117 in the OEIS)

Square-free factorization

Every positive integer [math]\displaystyle{ n }[/math] can be factored in a unique way as [math]\displaystyle{ n=\prod_{i=1}^k q_i^i, }[/math] where the [math]\displaystyle{ q_i }[/math] different from one are square-free integers that are pairwise coprime. This is called the square-free factorization of n.

To construct the square-free factorization, let [math]\displaystyle{ n=\prod_{j=1}^h p_j^{e_j} }[/math] be the prime factorization of [math]\displaystyle{ n }[/math], where the [math]\displaystyle{ p_j }[/math] are distinct prime numbers. Then the factors of the square-free factorization are defined as [math]\displaystyle{ q_i=\prod_{j: e_j=i}p_j. }[/math]

An integer is square-free if and only if [math]\displaystyle{ q_i=1 }[/math] for all [math]\displaystyle{ i \gt 1 }[/math]. An integer greater than one is the [math]\displaystyle{ k }[/math]th power of another integer if and only if [math]\displaystyle{ k }[/math] is a divisor of all [math]\displaystyle{ i }[/math] such that [math]\displaystyle{ q_i\neq 1. }[/math]

The use of the square-free factorization of integers is limited by the fact that its computation is as difficult as the computation of the prime factorization. More precisely every known algorithm for computing a square-free factorization computes also the prime factorization. This is a notable difference with the case of polynomials for which the same definitions can be given, but, in this case, the square-free factorization is not only easier to compute than the complete factorization, but it is the first step of all standard factorization algorithms.

Square-free factors of integers

The radical of an integer is its largest square-free factor, that is [math]\displaystyle{ \textstyle \prod_{i=1}^k q_i }[/math] with notation of the preceding section. An integer is square-free if and only if it is equal to its radical.

Every positive integer [math]\displaystyle{ n }[/math] can be represented in a unique way as the product of a powerful number (that is an integer such that is divisible by the square of every prime factor) and a square-free integer, which are coprime. In this factorization, the square-free factor is [math]\displaystyle{ q_1, }[/math] and the powerful number is [math]\displaystyle{ \textstyle \prod_{i=2}^k q_i^i. }[/math]

The square-free part of [math]\displaystyle{ n }[/math] is [math]\displaystyle{ q_1, }[/math] which is the largest square-free divisor [math]\displaystyle{ k }[/math] of [math]\displaystyle{ n }[/math] that is coprime with [math]\displaystyle{ n/k }[/math]. The square-free part of an integer may be smaller than the largest square-free divisor, which is [math]\displaystyle{ \textstyle \prod_{i=1}^k q_i. }[/math]

Any arbitrary positive integer [math]\displaystyle{ n }[/math] can be represented in a unique way as the product of a square and a square-free integer: [math]\displaystyle{ n=m^2 k }[/math] In this factorization, [math]\displaystyle{ m }[/math] is the largest divisor of [math]\displaystyle{ n }[/math] such that [math]\displaystyle{ m^2 }[/math] is a divisor of [math]\displaystyle{ n }[/math].

In summary, there are three square-free factors that are naturally associated to every integer: the square-free part, the above factor [math]\displaystyle{ k }[/math], and the largest square-free factor. Each is a factor of the next one. All are easily deduced from the prime factorization or the square-free factorization: if [math]\displaystyle{ n=\prod_{i=1}^h p_i^{e_i}=\prod_{i=1}^k q_i^i }[/math] are the prime factorization and the square-free factorization of [math]\displaystyle{ n }[/math], where [math]\displaystyle{ p_1, \ldots, p_h }[/math] are distinct prime numbers, then the square-free part is [math]\displaystyle{ \prod_{e_i=1} p_i =q_1, }[/math] The square-free factor such the quotient is a square is [math]\displaystyle{ \prod_{e_i \text{ odd}} p_i=\prod_{i \text{ odd}} q_i, }[/math] and the largest square-free factor is [math]\displaystyle{ \prod_{i=1}^h p_i=\prod_{i=1}^k q_i. }[/math]

For example, if [math]\displaystyle{ n=75600=2^4\cdot 3^3\cdot 5^2\cdot 7, }[/math] one has [math]\displaystyle{ q_1=7,\; q_2=5,\;q_3=3,\;q_4=2. }[/math] The square-free part is 7, the square-free factor such that the quotient is a square is 3 ⋅ 7 = 21, and the largest square-free factor is 2 ⋅ 3 ⋅ 5 ⋅ 7 = 210.

No algorithm is known for computing any of these square-free factors which is faster than computing the complete prime factorization. In particular, there is no known polynomial-time algorithm for computing the square-free part of an integer, or even for determining whether an integer is square-free. In contrast, polynomial-time algorithms are known for primality testing. This is a major difference between the arithmetic of the integers, and the arithmetic of the univariate polynomials, as polynomial-time algorithms are known for square-free factorization of polynomials (in short, the largest square-free factor of a polynomial is its quotient by the greatest common divisor of the polynomial and its formal derivative).

Equivalent characterizations

A positive integer [math]\displaystyle{ n }[/math] is square-free if and only if in the prime factorization of [math]\displaystyle{ n }[/math], no prime factor occurs with an exponent larger than one. Another way of stating the same is that for every prime factor [math]\displaystyle{ p }[/math] of [math]\displaystyle{ n }[/math], the prime [math]\displaystyle{ p }[/math] does not evenly divide [math]\displaystyle{ n/p }[/math]. Also [math]\displaystyle{ n }[/math] is square-free if and only if in every factorization [math]\displaystyle{ n=ab }[/math], the factors [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are coprime. An immediate result of this definition is that all prime numbers are square-free.

A positive integer [math]\displaystyle{ n }[/math] is square-free if and only if all abelian groups of order [math]\displaystyle{ n }[/math] are isomorphic, which is the case if and only if any such group is cyclic. This follows from the classification of finitely generated abelian groups.

A integer [math]\displaystyle{ n }[/math] is square-free if and only if the factor ring [math]\displaystyle{ \mathbb{Z}/n\mathbb{Z} }[/math] (see modular arithmetic) is a product of fields. This follows from the Chinese remainder theorem and the fact that a ring of the form [math]\displaystyle{ \mathbb{Z}/k\mathbb{Z} }[/math] is a field if and only if [math]\displaystyle{ k }[/math] is prime.

For every positive integer [math]\displaystyle{ n }[/math], the set of all positive divisors of [math]\displaystyle{ n }[/math] becomes a partially ordered set if we use divisibility as the order relation. This partially ordered set is always a distributive lattice. It is a Boolean algebra if and only if [math]\displaystyle{ n }[/math] is square-free.

A positive integer [math]\displaystyle{ n }[/math] is square-free if and only if [math]\displaystyle{ \mu(n)\ne 0 }[/math], where [math]\displaystyle{ \mu }[/math] denotes the Möbius function.

Dirichlet series

The absolute value of the Möbius function is the indicator function for the square-free integers – that is, ‹See Tfd›|μ(n)| is equal to 1 if n is square-free, and 0 if it is not. The Dirichlet series of this indicator function is

[math]\displaystyle{ \sum_{n=1}^{\infty}\frac{|\mu(n)|}{n^{s}} = \frac{\zeta(s)}{\zeta(2s)}, }[/math]

where ζ(s) is the Riemann zeta function. This follows from the Euler product

[math]\displaystyle{ \frac{\zeta(s)}{\zeta(2s) } =\prod_p \frac{(1-p^{-2s})}{(1-p^{-s})}=\prod_p (1+p^{-s}), }[/math]

where the products are taken over the prime numbers.

Distribution

Let Q(x) denote the number of square-free integers between 1 and x (OEIS: A013928 shifting index by 1). For large n, 3/4 of the positive integers less than n are not divisible by 4, 8/9 of these numbers are not divisible by 9, and so on. Because these ratios satisfy the multiplicative property (this follows from Chinese remainder theorem), we obtain the approximation:

[math]\displaystyle{ \begin{align}Q(x) &\approx x\prod_{p\ \text{prime}} \left(1-\frac{1}{p^2}\right) = x\prod_{p\ \text{prime}} \frac{1}{(1-\frac{1}{p^2})^{-1}}\\ &=x\prod_{p\ \text{prime}} \frac{1}{1+\frac{1}{p^2}+\frac{1}{p^4}+\cdots} = \frac{x}{\sum_{k=1}^\infty \frac{1}{k^2}} = \frac{x}{\zeta(2)} = \frac{6x}{\pi^2}.\end{align} }[/math]

This argument can be made rigorous for getting the estimate (using big O notation)

[math]\displaystyle{ Q(x) = \frac{6x}{\pi^2} + O\left(\sqrt{x}\right). }[/math]

Sketch of a proof: the above characterization gives

[math]\displaystyle{ Q(x)=\sum_{n\leq x} \sum_{d^2\mid n} \mu(d)=\sum_{d\leq x} \mu(d)\sum_{n\leq x, d^2\mid n}1=\sum_{d\leq x} \mu(d)\left\lfloor\frac{x}{d^2}\right\rfloor; }[/math]

observing that the last summand is zero for [math]\displaystyle{ d\gt \sqrt{x} }[/math], it results that

[math]\displaystyle{ \begin{align}Q(x)&=\sum_{d\leq\sqrt{x}} \mu(d)\left\lfloor\frac{x}{d^2}\right\rfloor =\sum_{d\leq\sqrt{x}} \frac{x\mu(d)}{d^2}+O\left(\sum_{d\leq\sqrt{x}} 1\right) =x\sum_{d\leq\sqrt{x}} \frac{\mu(d)}{d^2}+O(\sqrt{x})\\ &=x\sum_{d} \frac{\mu(d)}{d^2}+O\left(x\sum_{d\gt \sqrt{x}}\frac{1}{d^2}+\sqrt{x}\right) =\frac{x}{\zeta(2)}+O(\sqrt{x}). \end{align} }[/math]

By exploiting the largest known zero-free region of the Riemann zeta function Arnold Walfisz improved the approximation to

[math]\displaystyle{ Q(x) = \frac{6x}{\pi^2} + O\left(x^{1/2}\exp\left(-c\frac{(\log x)^{3/5}}{(\log\log x)^{1/5}}\right)\right), }[/math]

for some positive constant c.

Under the Riemann hypothesis, the error term can be reduced to

[math]\displaystyle{ Q(x) = \frac{x}{\zeta(2)} + O\left(x^{17/54+\varepsilon}\right) = \frac{6}{\pi^2}x + O\left(x^{17/54+\varepsilon}\right). }[/math]

In 2015 the error term was further reduced to

[math]\displaystyle{ Q(x) = \frac{6}{\pi^2}x + O\left(x^{11/35+\varepsilon}\right). }[/math]

The asymptotic/natural density of square-free numbers is therefore

[math]\displaystyle{ \lim_{x\to\infty} \frac{Q(x)}{x} = \frac{6}{\pi^2}\approx 0.6079 }[/math]

Therefore over 3/5 of the integers are square-free.

Likewise, if Q(x,n) denotes the number of n-free integers (e.g. 3-free integers being cube-free integers) between 1 and x, one can show

[math]\displaystyle{ Q(x,n) = \frac{x}{\sum_{k=1}^\infty \frac{1}{k^n}} + O\left(\sqrt[n]{x}\right) = \frac{x}{\zeta(n)} + O\left(\sqrt[n]{x}\right). }[/math]

Since a multiple of 4 must have a square factor 4=2², it cannot occur that four consecutive integers are all square-free. On the other hand, there exist infinitely many integers n for which 4n +1, 4n +2, 4n +3 are all square-free. Otherwise, observing that 4n and at least one of 4n +1, 4n +2, 4n +3 among four could be non-square-free for sufficiently large n, half of all positive integers minus finitely many must be non-square-free and therefore

[math]\displaystyle{ Q(x) \leq \frac{x}{2}+C }[/math] for some constant C,

contrary to the above asymptotic estimate for [math]\displaystyle{ Q(x) }[/math].

There exist sequences of consecutive non-square-free integers of arbitrary length. Indeed, if n satisfies a simultaneous congruence

[math]\displaystyle{ n\equiv -i\pmod{p_i^2} \qquad (i=1, 2, \ldots, l) }[/math]

for distinct primes [math]\displaystyle{ p_1, p_2, \ldots, p_l }[/math], then each [math]\displaystyle{ n+i }[/math] is divisible by p_i ². On the other hand, the above-mentioned estimate [math]\displaystyle{ Q(x) = 6x/\pi^2 + O\left(\sqrt{x}\right) }[/math] implies that, for some constant c, there always exists a square-free integer between x and [math]\displaystyle{ x+c\sqrt{x} }[/math] for positive x. Moreover, an elementary argument allows us to replace [math]\displaystyle{ x+c\sqrt{x} }[/math] by [math]\displaystyle{ x+cx^{1/5}\log x. }[/math] The ABC conjecture would allow [math]\displaystyle{ x+x^{o(1)} }[/math].

Table of Q(x), 6/π²x, and R(x)

The table shows how [math]\displaystyle{ Q(x) }[/math] and [math]\displaystyle{ \frac{6}{\pi^2}x }[/math] (with the latter rounded to one decimal place) compare at powers of 10.

[math]\displaystyle{ R(x) = Q(x) -\frac{6}{\pi^2}x }[/math] , also denoted as [math]\displaystyle{ \Delta(x) }[/math].

[math]\displaystyle{ x }[/math]	[math]\displaystyle{ Q(x) }[/math]	[math]\displaystyle{ \frac{6}{\pi^2}x }[/math]	[math]\displaystyle{ R(x) }[/math]
10	7	6.1	0.9
102	61	60.8	0.2
103	608	607.9	0.1
104	6,083	6,079.3	3.7
105	60,794	60,792.7	1.3
106	607,926	607,927.1	- 1.3
107	6,079,291	6,079,271.0	20.0
108	60,792,694	60,792,710.2	- 16.2
109	607,927,124	607,927,101.9	22.1
1010	6,079,270,942	6,079,271,018.5	- 76.5
1011	60,792,710,280	60,792,710,185.4	94.6
1012	607,927,102,274	607,927,101,854.0	420.0
1013	6,079,271,018,294	6,079,271,018,540.3	- 246.3
1014	60,792,710,185,947	60,792,710,185,402.7	544.3
1015	607,927,101,854,103	607,927,101,854,027.0	76.0

[math]\displaystyle{ R(x) }[/math] changes its sign infinitely often as [math]\displaystyle{ x }[/math] tends to infinity.

The absolute value of [math]\displaystyle{ R(x) }[/math] is astonishingly small compared with [math]\displaystyle{ x }[/math].

Encoding as binary numbers

If we represent a square-free number as the infinite product

[math]\displaystyle{ \prod_{n=0}^\infty (p_{n+1})^{a_n}, a_n \in \lbrace 0, 1 \rbrace,\text{ and }p_n\text{ is the }n\text{th prime}, }[/math]

then we may take those [math]\displaystyle{ a_n }[/math] and use them as bits in a binary number with the encoding

[math]\displaystyle{ \sum_{n=0}^\infty {a_n}\cdot 2^n . }[/math]

The square-free number 42 has factorization 2 × 3 × 7, or as an infinite product 2¹ · 3¹ · 5⁰ · 7¹ · 11⁰ · 13⁰ ··· Thus the number 42 may be encoded as the binary sequence ...001011 or 11 decimal. (The binary digits are reversed from the ordering in the infinite product.)

Since the prime factorization of every number is unique, so also is every binary encoding of the square-free integers.

The converse is also true. Since every positive integer has a unique binary representation it is possible to reverse this encoding so that they may be decoded into a unique square-free integer.

Again, for example, if we begin with the number 42, this time as simply a positive integer, we have its binary representation 101010. This decodes to 2⁰ · 3¹ · 5⁰ · 7¹ · 11⁰ · 13¹ = 3 × 7 × 13 = 273.

Thus binary encoding of squarefree numbers describes a bijection between the nonnegative integers and the set of positive squarefree integers.

(See sequences A019565, A048672 and A064273 in the OEIS.)

Erdős squarefree conjecture

The central binomial coefficient

[math]\displaystyle{ {2n \choose n} }[/math]

is never squarefree for n > 4. This was proven in 1985 for all sufficiently large integers by András Sárközy, and for all integers > 4 in 1996 by Olivier Ramaré and Andrew Granville.

Squarefree core

Let us call "t-free" a positive integer that has no t-th power in its divisors. In particular, the 2-free integers are the square-free integers.

The multiplicative function [math]\displaystyle{ \mathrm{core}_t(n) }[/math] maps every positive integer n to the quotient of n by its largest divisor that is a t-th power. That is,

[math]\displaystyle{ \mathrm{core}_t(p^e) = p^{e\bmod t}. }[/math]

The integer [math]\displaystyle{ \mathrm{core}_t(n) }[/math] is t-free, and every t-free integer is mapped to itself by the function [math]\displaystyle{ \mathrm{core}_t. }[/math]

The Dirichlet generating function of the sequence [math]\displaystyle{ \left(\mathrm{core}_t(n) \right)_{n\in \N} }[/math] is

[math]\displaystyle{ \sum_{n\ge 1}\frac{\mathrm{core}_t(n)}{n^s} = \frac{\zeta(ts)\zeta(s-1)}{\zeta(ts-t)} }[/math].

See also OEIS: A007913 (t=2), OEIS: A050985 (t=3) and OEIS: A053165 (t=4).

References

• Shapiro, Harold N. (1983). Introduction to the theory of numbers. Oxford University Press Dover Publications. ISBN 978-0-486-46669-9. 
• Granville, Andrew; Ramaré, Olivier (1996). "Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients". Mathematika 43: 73–107. doi:10.1112/S0025579300011608. 
• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. ISBN 978-0-387-20860-2. 
• "OEIS Wiki". http://oeis.org/wiki/Squarefree_numbers.