Harmonic divisor number

Short description: Positive integer whose divisors have a harmonic mean that is an integer

In mathematics, a harmonic divisor number or Ore number is a positive integer whose divisors have a harmonic mean that is an integer. The first few harmonic divisor numbers are

1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190 (sequence A001599 in the OEIS).

Harmonic divisor numbers were introduced by Øystein Ore, who showed that every perfect number is a harmonic divisor number and conjectured that there are no odd harmonic divisor numbers other than 1.

Examples

The number 6 has the four divisors 1, 2, 3, and 6. Their harmonic mean is an integer: [math]\displaystyle{ \frac{4}{\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{6}}=2. }[/math] Thus 6 is a harmonic divisor number. Similarly, the number 140 has divisors 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140. Their harmonic mean is [math]\displaystyle{ \frac{12}{\frac{1}{1}+\frac{1}{2}+\frac{1}{4}+\frac{1}{5}+\frac{1}{7}+\frac{1}{10} +\frac{1}{14}+\frac{1}{20}+\frac{1}{28}+\frac{1}{35}+\frac{1}{70}+\frac{1}{140}}=5. }[/math] Since 5 is an integer, 140 is a harmonic divisor number.

Factorization of the harmonic mean

The harmonic mean H(n) of the divisors of any number n can be expressed as the formula [math]\displaystyle{ H(n) = \frac{n\sigma_0(n)}{\sigma_1(n)} }[/math] where σ_i(n) is the sum of ith powers of the divisors of n: σ₀ is the number of divisors, and σ₁ is the sum of divisors (Cohen 1997). All of the terms in this formula are multiplicative but not completely multiplicative. Therefore, the harmonic mean H(n) is also multiplicative. This means that, for any positive integer n, the harmonic mean H(n) can be expressed as the product of the harmonic means of the prime powers in the factorization of n.

For instance, we have [math]\displaystyle{ H(4) = \frac{3}{1+\frac{1}{2}+\frac{1}{4}}=\frac{12}7, }[/math] [math]\displaystyle{ H(5) = \frac{2}{1+\frac{1}{5}} = \frac53, }[/math] [math]\displaystyle{ H(7) = \frac{2}{1+\frac{1}{7}} = \frac74, }[/math] and [math]\displaystyle{ H(140) = H(4 \cdot 5 \cdot 7) = H(4)\cdot H(5)\cdot H(7) = \frac{12}{7}\cdot \frac{5}{3}\cdot \frac{7}{4} = 5. }[/math]

Harmonic divisor numbers and perfect numbers

Demonstration, with Cuisenaire rods, of the perfection of the number 6

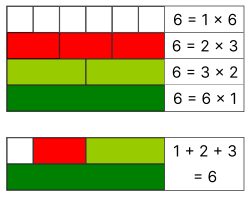
For any integer M, as Ore observed, the product of the harmonic mean and arithmetic mean of its divisors equals M itself, as can be seen from the definitions. Therefore, M is harmonic, with harmonic mean of divisors k, if and only if the average of its divisors is the product of M with a unit fraction 1/k.

Ore showed that every perfect number is harmonic. To see this, observe that the sum of the divisors of a perfect number M is exactly 2M; therefore, the average of the divisors is M(2/τ(M)), where τ(M) denotes the number of divisors of M. For any M, τ(M) is odd if and only if M is a square number, for otherwise each divisor d of M can be paired with a different divisor M/d. But no perfect number can be a square: this follows from the known form of even perfect numbers and from the fact that odd perfect numbers (if they exist) must have a factor of the form q^α where α ≡ 1 (mod 4). Therefore, for a perfect number M, τ(M) is even and the average of the divisors is the product of M with the unit fraction 2/τ(M); thus, M is a harmonic divisor number.

Ore conjectured that no odd harmonic divisor numbers exist other than 1. If the conjecture is true, this would imply the nonexistence of odd perfect numbers.

Bounds and computer searches

W. H. Mills (unpublished; see Muskat) showed that any odd harmonic divisor number above 1 must have a prime power factor greater than 10⁷, and Cohen showed that any such number must have at least three different prime factors. (Cohen Sorli) showed that there are no odd harmonic divisor numbers smaller than 10²⁴.

Cohen, Goto, and others starting with Ore himself have performed computer searches listing all small harmonic divisor numbers. From these results, lists are known of all harmonic divisor numbers up to 2 × 10⁹, and all harmonic divisor numbers for which the harmonic mean of the divisors is at most 300.

References

• Bogomolny, Alexander. "An Identity Concerning Averages of Divisors of a Given Integer". http://www.cut-the-knot.org/proofs/average.shtml. 
• Cohen, Graeme L. (1997). "Numbers Whose Positive Divisors Have Small Integral Harmonic Mean". Mathematics of Computation 66 (218): 883–891. doi:10.1090/S0025-5718-97-00819-3. https://www.ams.org/mcom/1997-66-218/S0025-5718-97-00819-3/S0025-5718-97-00819-3.pdf. 
• Cohen, Graeme L.; Sorli, Ronald M. (2010). "Odd harmonic numbers exceed 10²⁴". Mathematics of Computation 79 (272): 2451. doi:10.1090/S0025-5718-10-02337-9. ISSN 0025-5718. 
• Goto, Takeshi. "(Ore's) Harmonic Numbers". http://www.ma.noda.tus.ac.jp/u/tg/harmonic-e.html. 
• Guy, Richard K. (2004). Unsolved problems in number theory (3rd ed.). Springer-Verlag. B2. ISBN 978-0-387-20860-2. 
• Muskat, Joseph B. (1966). "On Divisors of Odd Perfect Numbers". Mathematics of Computation 20 (93): 141–144. doi:10.2307/2004277. 
• Ore, Øystein (1948). "On the averages of the divisors of a number". American Mathematical Monthly 55 (10): 615–619. doi:10.2307/2305616. 
• Weisstein, Eric W.. "Harmonic Divisor Number". http://mathworld.wolfram.com/HarmonicDivisorNumber.html.