Weird number
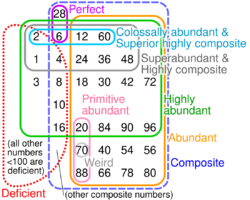
In number theory, a weird number is a natural number that is abundant but not semiperfect.[1][2] In other words, the sum of the proper divisors (divisors including 1 but not itself) of the number is greater than the number, but no subset of those divisors sums to the number itself.
Examples
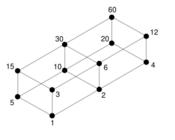
The smallest weird number is 70. Its proper divisors are 1, 2, 5, 7, 10, 14, and 35; these sum to 74, but no subset of these sums to 70. The number 12, for example, is abundant but not weird, because the proper divisors of 12 are 1, 2, 3, 4, and 6, which sum to 16; but 2 + 4 + 6 = 12.
The first few weird numbers are
- 70, 836, 4030, 5830, 7192, 7912, 9272, 10430, 10570, 10792, 10990, 11410, 11690, 12110, 12530, 12670, 13370, 13510, 13790, 13930, 14770, ... (sequence A006037 in the OEIS).
Properties
| Unsolved problem in mathematics: Are there any odd weird numbers? (more unsolved problems in mathematics)
|
Infinitely many weird numbers exist.[3] For example, 70p is weird for all primes p ≥ 149. In fact, the set of weird numbers has positive asymptotic density.[4]
It is not known if any odd weird numbers exist. If so, they must be greater than 1021.[5]
Sidney Kravitz has shown that for k a positive integer, Q a prime exceeding 2k, and
- [math]\displaystyle{ R = \frac{2^kQ-(Q+1)}{(Q+1)-2^k} }[/math]
also prime and greater than 2k, then
- [math]\displaystyle{ n = 2^{k-1}QR }[/math]
is a weird number.[6] With this formula, he found the large weird number
- [math]\displaystyle{ n=2^{56}\cdot(2^{61}-1)\cdot153722867280912929\ \approx\ 2\cdot10^{52}. }[/math]
Primitive weird numbers
A property of weird numbers is that if n is weird, and p is a prime greater than the sum of divisors σ(n), then pn is also weird.[4] This leads to the definition of primitive weird numbers: weird numbers that are not a multiple of other weird numbers (sequence A002975 in the OEIS). Among the 1765 weird numbers less than one million, there are 24 primitive weird numbers. The construction of Kravitz yields primitive weird numbers, since all weird numbers of the form [math]\displaystyle{ 2^k p q }[/math] are primitive, but the existence of infinitely many k and Q which yield a prime R is not guaranteed. It is conjectured that there exist infinitely many primitive weird numbers, and Melfi has shown that the infiniteness of primitive weird numbers is a consequence of Cramér's conjecture.[7] Primitive weird numbers with as many as 16 prime factors and 14712 digits have been found.[8]
See also
References
- ↑ Benkoski, Stan (August–September 1972). "E2308 (in Problems and Solutions)". The American Mathematical Monthly 79 (7): 774. doi:10.2307/2316276.
- ↑ Richard K. Guy (2004). Unsolved Problems in Number Theory. Springer-Verlag. ISBN 0-387-20860-7. OCLC 54611248. Section B2.
- ↑ Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. pp. 113–114. ISBN 1-4020-4215-9.
- ↑ 4.0 4.1 Benkoski, Stan; Erdős, Paul (April 1974). "On Weird and Pseudoperfect Numbers". Mathematics of Computation 28 (126): 617–623. doi:10.2307/2005938.
- ↑ Sloane, N. J. A., ed. "Sequence A006037 (Weird numbers: abundant (A005101) but not pseudoperfect (A005835))". OEIS Foundation. https://oeis.org/A006037. -- comments concerning odd weird numbers
- ↑ Kravitz, Sidney (1976). "A search for large weird numbers". Journal of Recreational Mathematics (Baywood Publishing) 9 (2): 82–85.
- ↑ Melfi, Giuseppe (2015). "On the conditional infiniteness of primitive weird numbers". Journal of Number Theory (Elsevier) 147: 508–514. doi:10.1016/j.jnt.2014.07.024.
- ↑ Amato, Gianluca; Hasler, Maximilian; Melfi, Giuseppe; Parton, Maurizio (2019). "Primitive abundant and weird numbers with many prime factors". Journal of Number Theory (Elsevier) 201: 436–459. doi:10.1016/j.jnt.2019.02.027.
External links
 |