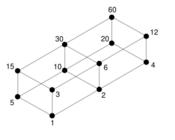
Regular number
Regular numbers are numbers that evenly divide powers of 60 (or, equivalently, powers of 30). Equivalently, they are the numbers whose only prime divisors are 2, 3, and 5. As an example, 602 = 3600 = 48 × 75, so as divisors of a power of 60 both 48 and 75 are regular.
These numbers arise in several areas of mathematics and its applications, and have different names coming from their different areas of study.
- In number theory, these numbers are called 5-smooth, because they can be characterized as having only 2, 3, or 5 as their prime factors. This is a specific case of the more general k-smooth numbers, the numbers that have no prime factor greater than k.
- In the study of Babylonian mathematics, the divisors of powers of 60 are called regular numbers or regular sexagesimal numbers, and are of great importance in this area because of the sexagesimal (base 60) number system that the Babylonians used for writing their numbers, and that was central to Babylonian mathematics.
- In music theory, regular numbers occur in the ratios of tones in five-limit just intonation. In connection with music theory and related theories of architecture, these numbers have been called the harmonic whole numbers.
- In computer science, regular numbers are often called Hamming numbers, after Richard Hamming, who proposed the problem of finding computer algorithms for generating these numbers in ascending order. This problem has been used as a test case for functional programming.
Number theory
Formally, a regular number is an integer of the form [math]\displaystyle{ 2^i\cdot 3^j\cdot 5^k }[/math], for nonnegative integers [math]\displaystyle{ i }[/math], [math]\displaystyle{ j }[/math], and [math]\displaystyle{ k }[/math]. Such a number is a divisor of [math]\displaystyle{ 60^{\max(\lceil i\,/2\rceil,j,k)} }[/math]. The regular numbers are also called 5-smooth, indicating that their greatest prime factor is at most 5.[2] More generally, a k-smooth number is a number whose greatest prime factor is at most k.[3]
The first few regular numbers are[2]
Several other sequences at the On-Line Encyclopedia of Integer Sequences have definitions involving 5-smooth numbers.[4]
Although the regular numbers appear dense within the range from 1 to 60, they are quite sparse among the larger integers. A regular number [math]\displaystyle{ n=2^i\cdot 3^j\cdot 5^k }[/math] is less than or equal to some threshold [math]\displaystyle{ N }[/math] if and only if the point [math]\displaystyle{ (i,j,k) }[/math] belongs to the tetrahedron bounded by the coordinate planes and the plane [math]\displaystyle{ i\ln 2+j\ln 3+k\ln 5\le\ln N, }[/math] as can be seen by taking logarithms of both sides of the inequality [math]\displaystyle{ 2^i\cdot 3^j\cdot 5^k\le N }[/math]. Therefore, the number of regular numbers that are at most [math]\displaystyle{ N }[/math] can be estimated as the volume of this tetrahedron, which is [math]\displaystyle{ \frac{\log_2 N\,\log_3 N\,\log_5 N}{6}. }[/math] Even more precisely, using big O notation, the number of regular numbers up to [math]\displaystyle{ N }[/math] is [math]\displaystyle{ \frac{\left(\ln(N\sqrt{30})\right)^3}{6\ln 2 \ln 3 \ln 5}+O(\log N), }[/math] and it has been conjectured that the error term of this approximation is actually [math]\displaystyle{ O(\log\log N) }[/math].[2] A similar formula for the number of 3-smooth numbers up to [math]\displaystyle{ N }[/math] is given by Srinivasa Ramanujan in his first letter to G. H. Hardy.[5]
Babylonian mathematics
In the Babylonian sexagesimal notation, the reciprocal of a regular number has a finite representation. If [math]\displaystyle{ n }[/math] divides [math]\displaystyle{ 60^k }[/math], then the sexagesimal representation of [math]\displaystyle{ 1/n }[/math] is just that for [math]\displaystyle{ 60^k/n }[/math], shifted by some number of places. This allows for easy division by these numbers: to divide by [math]\displaystyle{ n }[/math], multiply by [math]\displaystyle{ 1/n }[/math], then shift.[6]
For instance, consider division by the regular number 54 = 2133. 54 is a divisor of 603, and 603/54 = 4000, so dividing by 54 in sexagesimal can be accomplished by multiplying by 4000 and shifting three places. In sexagesimal 4000 = 1×3600 + 6×60 + 40×1, or (as listed by Joyce) 1:6:40. Thus, 1/54, in sexagesimal, is 1/60 + 6/602 + 40/603, also denoted 1:6:40 as Babylonian notational conventions did not specify the power of the starting digit. Conversely 1/4000 = 54/603, so division by 1:6:40 = 4000 can be accomplished by instead multiplying by 54 and shifting three sexagesimal places.
The Babylonians used tables of reciprocals of regular numbers, some of which still survive.[7] These tables existed relatively unchanged throughout Babylonian times.[6] One tablet from Seleucid times, by someone named Inaqibıt-Anu, contains the reciprocals of 136 of the 231 six-place regular numbers whose first place is 1 or 2, listed in order. It also includes reciprocals of some numbers of more than six places, such as 323 (2 1 4 8 3 0 7 in sexagesimal), whose reciprocal has 17 sexagesimal digits. Noting the difficulty of both calculating these numbers and sorting them, Donald Knuth in 1972 hailed Inaqibıt-Anu as "the first man in history to solve a computational problem that takes longer than one second of time on a modern electronic computer!" (Two tables are also known giving approximations of reciprocals of non-regular numbers, one of which gives reciprocals for all the numbers from 56 to 80.)[8][9]
Although the primary reason for preferring regular numbers to other numbers involves the finiteness of their reciprocals, some Babylonian calculations other than reciprocals also involved regular numbers. For instance, tables of regular squares have been found[6] and the broken tablet Plimpton 322 has been interpreted by Neugebauer as listing Pythagorean triples [math]\displaystyle{ ( p^2 - q^2,\, 2pq,\, p^2 + q^2 ) }[/math] generated by [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] both regular and less than 60.[10] Fowler and Robson discuss the calculation of square roots, such as how the Babylonians found an approximation to the square root of 2, perhaps using regular number approximations of fractions such as 17/12.[9]
Music theory
In music theory, the just intonation of the diatonic scale involves regular numbers: the pitches in a single octave of this scale have frequencies proportional to the numbers in the sequence 24, 27, 30, 32, 36, 40, 45, 48 of nearly consecutive regular numbers.[11] Thus, for an instrument with this tuning, all pitches are regular-number harmonics of a single fundamental frequency. This scale is called a 5-limit tuning, meaning that the interval between any two pitches can be described as a product 2i3j5k of powers of the prime numbers up to 5, or equivalently as a ratio of regular numbers.[12]
5-limit musical scales other than the familiar diatonic scale of Western music have also been used, both in traditional musics of other cultures and in modern experimental music: (Honingh Bod) list 31 different 5-limit scales, drawn from a larger database of musical scales. Each of these 31 scales shares with diatonic just intonation the property that all intervals are ratios of regular numbers.[12] Euler's tonnetz provides a convenient graphical representation of the pitches in any 5-limit tuning, by factoring out the octave relationships (powers of two) so that the remaining values form a planar grid.[12] Some music theorists have stated more generally that regular numbers are fundamental to tonal music itself, and that pitch ratios based on primes larger than 5 cannot be consonant.[13] However the equal temperament of modern pianos is not a 5-limit tuning,[14] and some modern composers have experimented with tunings based on primes larger than five.[15]
In connection with the application of regular numbers to music theory, it is of interest to find pairs of regular numbers that differ by one. There are exactly ten such pairs [math]\displaystyle{ (x,x+1) }[/math] and each such pair defines a superparticular ratio [math]\displaystyle{ \tfrac{x+1}{x} }[/math] that is meaningful as a musical interval. These intervals are 2/1 (the octave), 3/2 (the perfect fifth), 4/3 (the perfect fourth), 5/4 (the just major third), 6/5 (the just minor third), 9/8 (the just major tone), 10/9 (the just minor tone), 16/15 (the just diatonic semitone), 25/24 (the just chromatic semitone), and 81/80 (the syntonic comma).[16]
In the Renaissance theory of universal harmony, musical ratios were used in other applications, including the architecture of buildings. In connection with the analysis of these shared musical and architectural ratios, for instance in the architecture of Palladio, the regular numbers have also been called the harmonic whole numbers.[17]
Algorithms
Algorithms for calculating the regular numbers in ascending order were popularized by Edsger Dijkstra. Dijkstra (1976, 1981) attributes to Hamming the problem of building the infinite ascending sequence of all 5-smooth numbers; this problem is now known as Hamming's problem, and the numbers so generated are also called the Hamming numbers. Dijkstra's ideas to compute these numbers are the following:
- The sequence of Hamming numbers begins with the number 1.
- The remaining values in the sequence are of the form [math]\displaystyle{ 2h }[/math], [math]\displaystyle{ 3h }[/math], and [math]\displaystyle{ 5h }[/math], where [math]\displaystyle{ h }[/math] is any Hamming number.
- Therefore, the sequence [math]\displaystyle{ H }[/math] may be generated by outputting the value 1, and then merging the sequences [math]\displaystyle{ 2H }[/math], [math]\displaystyle{ 3H }[/math], and [math]\displaystyle{ 5H }[/math].
This algorithm is often used to demonstrate the power of a lazy functional programming language, because (implicitly) concurrent efficient implementations, using a constant number of arithmetic operations per generated value, are easily constructed as described above. Similarly efficient strict functional or imperative sequential implementations are also possible whereas explicitly concurrent generative solutions might be non-trivial.[18]
In the Python programming language, lazy functional code for generating regular numbers is used as one of the built-in tests for correctness of the language's implementation.[19]
A related problem, discussed by (Knuth 1972), is to list all [math]\displaystyle{ k }[/math]-digit sexagesimal numbers in ascending order (see #Babylonian mathematics above). In algorithmic terms, this is equivalent to generating (in order) the subsequence of the infinite sequence of regular numbers, ranging from [math]\displaystyle{ 60^k }[/math] to [math]\displaystyle{ 60^{k+1} }[/math].[8] See (Gingerich 1965) for an early description of computer code that generates these numbers out of order and then sorts them;[20] Knuth describes an ad hoc algorithm, which he attributes to (Bruins 1970), for generating the six-digit numbers more quickly but that does not generalize in a straightforward way to larger values of [math]\displaystyle{ k }[/math].[8] (Eppstein 2007) describes an algorithm for computing tables of this type in linear time for arbitrary values of [math]\displaystyle{ k }[/math].[21]
Other applications
(Heninger Rains) show that, when [math]\displaystyle{ n }[/math] is a regular number and is divisible by 8, the generating function of an [math]\displaystyle{ n }[/math]-dimensional extremal even unimodular lattice is an [math]\displaystyle{ n }[/math]th power of a polynomial.[22]
As with other classes of smooth numbers, regular numbers are important as problem sizes in computer programs for performing the fast Fourier transform, a technique for analyzing the dominant frequencies of signals in time-varying data. For instance, the method of (Temperton 1992) requires that the transform length be a regular number.[23]
Book VIII of Plato's Republic involves an allegory of marriage centered on the highly regular number 604 = 12,960,000 and its divisors (see Plato's number). Later scholars have invoked both Babylonian mathematics and music theory in an attempt to explain this passage.[24]
Certain species of bamboo release large numbers of seeds in synchrony (a process called masting) at intervals that have been estimated as regular numbers of years, with different intervals for different species, including examples with intervals of 10, 15, 16, 30, 32, 48, 60, and 120 years.[25] It has been hypothesized that the biological mechanism for timing and synchronizing this process lends itself to smooth numbers, and in particular in this case to 5-smooth numbers. Although the estimated masting intervals for some other species of bamboo are not regular numbers of years, this may be explainable as measurement error.[25]
Notes
- ↑ Inspired by similar diagrams by Erkki Kurenniemi in "Chords, scales, and divisor lattices".
- ↑ Jump up to: 2.0 2.1 2.2 Sloane "A051037".
- ↑ Pomerance (1995).
- ↑ OEIS search for sequences involving 5-smoothness.
- ↑ Berndt & Rankin (1995).
- ↑ Jump up to: 6.0 6.1 6.2 Aaboe (1965).
- ↑ Sachs (1947).
- ↑ Jump up to: 8.0 8.1 8.2 Knuth (1972).
- ↑ Jump up to: 9.0 9.1 Fowler & Robson (1998).
- ↑ See (Conway Guy) for a popular treatment of this interpretation. Plimpton 322 has other interpretations, for which see its article, but all involve regular numbers.
- ↑ Clarke (1877).
- ↑ Jump up to: 12.0 12.1 12.2 Honingh & Bod (2005).
- ↑ (Asmussen 2001), for instance, states that "within any piece of tonal music" all intervals must be ratios of regular numbers, echoing similar statements by much earlier writers such as (Habens 1889). In the modern music theory literature this assertion is often attributed to (Longuet-Higgins 1962), who used a graphical arrangement closely related to the tonnetz to organize 5-limit pitches.
- ↑ Kopiez (2003).
- ↑ Wolf (2003).
- ↑ (Halsey Hewitt) note that this follows from Størmer's theorem (Størmer 1897), and provide a proof for this case; see also (Silver 1971).
- ↑ Howard & Longair (1982).
- ↑ See, e.g., (Hemmendinger 1988) or (Yuen 1992).
- ↑ Function m235 in test_generators.py.
- ↑ Gingerich (1965).
- ↑ Eppstein (2007).
- ↑ Heninger, Rains & Sloane (2006).
- ↑ Temperton (1992).
- ↑ (Barton 1908); (McClain 1974).
- ↑ Jump up to: 25.0 25.1 Veller, Nowak & Davis (2015).
References
- Aaboe, Asger (1965), "Some Seleucid mathematical tables (extended reciprocals and squares of regular numbers)", Journal of Cuneiform Studies (The American Schools of Oriental Research) 19 (3): 79–86, doi:10.2307/1359089.
- Asmussen, Robert (2001), Periodicity of sinusoidal frequencies as a basis for the analysis of Baroque and Classical harmony: a computer based study, Ph.D. thesis, University of Leeds, http://www.terraworld.net/c-jasmussen/thesis_asmussen.pdf.
- Barton, George A. (1908), "On the Babylonian origin of Plato's nuptial number", Journal of the American Oriental Society (American Oriental Society) 29: 210–219, doi:10.2307/592627.
- Berndt, Bruce C.; Rankin, Robert Alexander, eds. (1995), Ramanujan: letters and commentary, History of mathematics, 9, American Mathematical Society, p. 23, ISBN 978-0-8218-0470-4, Bibcode: 1995rlc..book.....B.
- Bruins, E. M. (1970), "La construction de la grande table le valeurs réciproques AO 6456", in Finet, André, Actes de la XVIIe Rencontre Assyriologique Internationale, Comité belge de recherches en Mésopotamie, pp. 99–115.
- Clarke, A. R. (January 1877), "Just intonation", Nature 15 (377): 253, doi:10.1038/015253b0, Bibcode: 1877Natur..15..253C.
- Conway, John H.; Guy, Richard K. (1996), The Book of Numbers, Copernicus, pp. 172–176, ISBN 0-387-97993-X, https://archive.org/details/bookofnumbers0000conw/page/172.
- Dijkstra, Edsger W. (1976), "17. An exercise attributed to R. W. Hamming", A Discipline of Programming, Prentice-Hall, pp. 129–134, ISBN 978-0132158718, https://archive.org/details/disciplineofprog0000dijk/page/129
- Hamming's exercise in SASL, 1981, Report EWD792. Originally a privately circulated handwritten note, http://www.cs.utexas.edu/users/EWD/ewd07xx/EWD792.PDF.
- Eppstein, David (2007), The range-restricted Hamming problem, https://11011110.github.io/blog/2007/03/18/range-restricted-hamming-problem.html.
- Fowler, David; Robson, Eleanor (1998), "Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context", Historia Mathematica 25 (4): 366–378, doi:10.1006/hmat.1998.2209, https://www.sciencedirect.com/science/article/pii/S0315086098922091/pdf?md5=7c3e116fac2deef21b107b78f3561862&pid=1-s2.0-S0315086098922091-main.pdf, page 375.
- Gingerich, Owen (1965), "Eleven-digit regular sexagesimals and their reciprocals", Transactions of the American Philosophical Society (American Philosophical Society) 55 (8): 3–38, doi:10.2307/1006080.
- Habens, Rev. W. J. (1889), "On the musical scale", Proceedings of the Musical Association (Royal Musical Association) 16: 16th Session, p. 1, https://zenodo.org/record/2404277.
- Halsey, G. D.; Hewitt, Edwin (1972), "More on the superparticular ratios in music", American Mathematical Monthly (Mathematical Association of America) 79 (10): 1096–1100, doi:10.2307/2317424.
- Hemmendinger, David (1988), "The "Hamming problem" in Prolog", ACM SIGPLAN Notices 23 (4): 81–86, doi:10.1145/44326.44335.
- "On the integrality of nth roots of generating functions", Journal of Combinatorial Theory, Series A 113 (8): 1732–1745, 2006, doi:10.1016/j.jcta.2006.03.018}.
- Honingh, Aline; Bod, Rens (2005), "Convexity and the well-formedness of musical objects", Journal of New Music Research 34 (3): 293–303, doi:10.1080/09298210500280612.
- "Harmonic proportion and Palladio's Quattro Libri", Journal of the Society of Architectural Historians 41 (2): 116–143, May 1982, doi:10.2307/989675
- "Ancient Babylonian algorithms", Communications of the ACM 15 (7): 671–677, 1972, doi:10.1145/361454.361514, https://teaching.csse.uwa.edu.au/units/CITS1001/extension/ancient-babylonian-algorithms.pdf. A correction appears in CACM 19(2), 1976, stating that the tablet does not contain all 231 of the numbers of interest. The article (corrected) with a brief addendum appears in Selected Papers on Computer Science, CSLI Lecture Notes 59, Cambridge Univ. Press, 1996, pp. 185–203, but without the Appendix that was included in the original paper.
- Kopiez, Reinhard (2003), "Intonation of harmonic intervals: adaptability of expert musicians to equal temperament and just intonation", Music Perception 20 (4): 383–410, doi:10.1525/mp.2003.20.4.383
- "Letter to a musical friend", Music Review (August): 244–248, 1962.
- McClain, Ernest G. (1974), "Musical "Marriages" in Plato's "Republic"", Journal of Music Theory (Duke University Press) 18 (2): 242–272, doi:10.2307/843638.
- "The role of smooth numbers in number-theoretic algorithms", Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Zürich, 1994), Basel: Birkhäuser, 1995, pp. 411–422.
- Sachs, A. J. (1947), "Babylonian mathematical texts. I. Reciprocals of regular sexagesimal numbers", Journal of Cuneiform Studies (The American Schools of Oriental Research) 1 (3): 219–240, doi:10.2307/1359434.
- Silver, A. L. Leigh (1971), "Musimatics or the nun's fiddle", American Mathematical Monthly (Mathematical Association of America) 78 (4): 351–357, doi:10.2307/2316896.
- Sloane, N. J. A., ed. "Sequence A051037 (5-smooth numbers)". OEIS Foundation. https://oeis.org/A051037.
- Størmer, Carl (1897), "Quelques théorèmes sur l'équation de Pell x2 − Dy2 = ±1 et leurs applications", Skrifter Videnskabs-selskabet (Christiania), Mat.-Naturv. Kl. I (2).
- Temperton, Clive (1992), "A generalized prime factor FFT algorithm for any N = 2p3q5r", SIAM Journal on Scientific and Statistical Computing 13 (3): 676–686, doi:10.1137/0913039.
- Veller, Carl; Nowak, Martin A.; Davis, Charles C. (May 2015), "Extended flowering intervals of bamboos evolved by discrete multiplication", Ecology Letters 18 (7): 653–659, doi:10.1111/ele.12442, PMID 25963600
- Wolf, Daniel James (March 2003), "Alternative tunings, alternative tonalities", Contemporary Music Review 22 (1–2): 3–14, doi:10.1080/0749446032000134715
- Yuen, C. K. (1992), "Hamming numbers, lazy evaluation, and eager disposal", ACM SIGPLAN Notices 27 (8): 71–75, doi:10.1145/142137.142151.
External links
- Table of reciprocals of regular numbers up to 3600 from the web site of Professor David E. Joyce, Clark University.
- RosettaCode Generation of Hamming_numbers in ~ 50 programming languages
 |