Hemiperfect number

In number theory, a hemiperfect number is a positive integer with a half-integer abundancy index. In other words, σ(n)/n = k/2 for an odd integer k, where σ(n) is the divisor function, the sum of all positive divisors of n. The first few hemiperfect numbers are:

2, 24, 4320, 4680, 26208, 8910720, 17428320, 20427264, 91963648, 197064960, ... (sequence A159907 in the OEIS)

Example

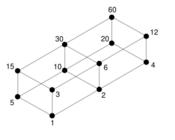
24 is a hemiperfect number because the sum of the divisors of 24 is

1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60 = 5/2 × 24.

The abundancy index is 5/2 which is a half-integer.

Smallest hemiperfect numbers of abundancy k/2

The following table gives an overview of the smallest hemiperfect numbers of abundancy k/2 for k ≤ 13 (sequence A088912 in the OEIS):

k	Smallest number of abundancy k/2	Number of digits
3	2	1
5	24	2
7	4320	4
9	8910720	7
11	17116004505600	14
13	170974031122008628879954060917200710847692800	45

The current best known upper bounds for the smallest numbers of abundancy 15/2 and 17/2 were found by Michel Marcus.

The smallest known number of abundancy 15/2 is ≈ 1.274947×10⁸⁸, and the smallest known number of abundancy 17/2 is ≈ 2.717290×10¹⁹⁰.

There are no known numbers of abundancy 19/2.

See also

• Semiperfect number
• Perfect number
• Multiply perfect number