Perfect number

Short description: Integer equal to the sum of its proper divisors

Illustration of the perfect number status of the number 6

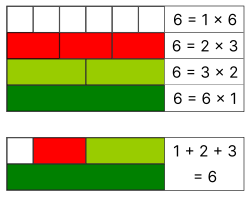
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.

The sum of divisors of a number, excluding the number itself, is called its aliquot sum, so a perfect number is one that is equal to its aliquot sum. Equivalently, a perfect number is a number that is half the sum of all of its positive divisors including itself; in symbols, [math]\displaystyle{ \sigma_1(n)=2n }[/math] where [math]\displaystyle{ \sigma_1 }[/math] is the sum-of-divisors function. For instance, 28 is perfect as 1 + 2 + 4 + 7 + 14 = 28.

This definition is ancient, appearing as early as Euclid's Elements (VII.22) where it is called τέλειος ἀριθμός (perfect, ideal, or complete number). Euclid also proved a formation rule (IX.36) whereby [math]\displaystyle{ q(q+1)/2 }[/math] is an even perfect number whenever [math]\displaystyle{ q }[/math] is a prime of the form [math]\displaystyle{ 2^p-1 }[/math] for positive integer [math]\displaystyle{ p }[/math]—what is now called a Mersenne prime. Two millennia later, Leonhard Euler proved that all even perfect numbers are of this form. This is known as the Euclid–Euler theorem.

It is not known whether there are any odd perfect numbers, nor whether infinitely many perfect numbers exist. The first few perfect numbers are 6, 28, 496 and 8128 (sequence A000396 in the OEIS).

History

In about 300 BC Euclid showed that if 2^p − 1 is prime then 2^p−1(2^p − 1) is perfect. The first four perfect numbers were the only ones known to early Greek mathematics, and the mathematician Nicomachus noted 8128 as early as around AD 100. In modern language, Nicomachus states without proof that every perfect number is of the form [math]\displaystyle{ 2^{n-1}(2^n-1) }[/math] where [math]\displaystyle{ 2^n-1 }[/math] is prime. He seems to be unaware that n itself has to be prime. He also says (wrongly) that the perfect numbers end in 6 or 8 alternately. (The first 5 perfect numbers end with digits 6, 8, 6, 8, 6; but the sixth also ends in 6.) Philo of Alexandria in his first-century book "On the creation" mentions perfect numbers, claiming that the world was created in 6 days and the moon orbits in 28 days because 6 and 28 are perfect. Philo is followed by Origen, and by Didymus the Blind, who adds the observation that there are only four perfect numbers that are less than 10,000. (Commentary on Genesis 1. 14–19). St Augustine defines perfect numbers in City of God (Book XI, Chapter 30) in the early 5th century AD, repeating the claim that God created the world in 6 days because 6 is the smallest perfect number. The Egyptian mathematician Ismail ibn Fallūs (1194–1252) mentioned the next three perfect numbers (33,550,336; 8,589,869,056; and 137,438,691,328) and listed a few more which are now known to be incorrect. The first known European mention of the fifth perfect number is a manuscript written between 1456 and 1461 by an unknown mathematician. In 1588, the Italian mathematician Pietro Cataldi identified the sixth (8,589,869,056) and the seventh (137,438,691,328) perfect numbers, and also proved that every perfect number obtained from Euclid's rule ends with a 6 or an 8.

Even perfect numbers

Unsolved problem in mathematics: Are there infinitely many perfect numbers? (more unsolved problems in mathematics)

Euclid proved that [math]\displaystyle{ 2^{p-1}(2^p-1) }[/math] is an even perfect number whenever [math]\displaystyle{ 2^p-1 }[/math] is prime (Elements, Prop. IX.36).

For example, the first four perfect numbers are generated by the formula [math]\displaystyle{ 2^{p-1}(2^p-1), }[/math] with p a prime number, as follows: [math]\displaystyle{ \begin{align} p = 2 &: \quad 2^1(2^2 - 1) = 2 \times 3 = 6 \\ p = 3 &: \quad 2^2(2^3 - 1) = 4 \times 7 = 28 \\ p = 5 &: \quad 2^4(2^5 - 1) = 16 \times 31 = 496 \\ p = 7 &: \quad 2^6(2^7 - 1) = 64 \times 127 = 8128. \end{align} }[/math]

Prime numbers of the form [math]\displaystyle{ 2^p-1 }[/math] are known as Mersenne primes, after the seventeenth-century monk Marin Mersenne, who studied number theory and perfect numbers. For [math]\displaystyle{ 2^p-1 }[/math] to be prime, it is necessary that p itself be prime. However, not all numbers of the form [math]\displaystyle{ 2^p-1 }[/math] with a prime p are prime; for example, 2¹¹ − 1 = 2047 = 23 × 89 is not a prime number. In fact, Mersenne primes are very rare—of the 2,610,944 prime numbers p up to 43,112,609, [math]\displaystyle{ 2^p-1 }[/math] is prime for only 47 of them.

While Nicomachus had stated (without proof) that all perfect numbers were of the form [math]\displaystyle{ 2^{n-1}(2^n-1) }[/math] where [math]\displaystyle{ 2^n-1 }[/math] is prime (though he stated this somewhat differently), Ibn al-Haytham (Alhazen) circa AD 1000 was unwilling to go that far, declaring instead (also without proof) that the formula yielded only every even perfect number. It was not until the 18th century that Leonhard Euler proved that the formula [math]\displaystyle{ 2^{p-1}(2^p-1) }[/math] will yield all the even perfect numbers. Thus, there is a one-to-one correspondence between even perfect numbers and Mersenne primes; each Mersenne prime generates one even perfect number, and vice versa. This result is often referred to as the Euclid–Euler theorem.

An exhaustive search by the GIMPS distributed computing project has shown that the first 48 even perfect numbers are [math]\displaystyle{ 2^{p-1}(2^p-1) }[/math] for

p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917, 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 42643801, 43112609 and 57885161 (sequence A000043 in the OEIS).

Three higher perfect numbers have also been discovered, namely those for which p = 74207281, 77232917, and 82589933. Although it is still possible there may be others within this range, initial but exhaustive tests by GIMPS have revealed no other perfect numbers for p below 109332539. (As of December 2018), 51 Mersenne primes are known, and therefore 51 even perfect numbers (the largest of which is 2^82589932 × (2^82589933 − 1) with 49,724,095 digits). It is not known whether there are infinitely many perfect numbers, nor whether there are infinitely many Mersenne primes.

As well as having the form [math]\displaystyle{ 2^{p-1}(2^p-1) }[/math], each even perfect number is the [math]\displaystyle{ (2^p-1) }[/math]-th triangular number (and hence equal to the sum of the integers from 1 to [math]\displaystyle{ 2^p-1 }[/math]) and the [math]\displaystyle{ 2^{p-1} }[/math]-th hexagonal number. Furthermore, each even perfect number except for 6 is the [math]\displaystyle{ \tfrac{2^p+1}{3} }[/math]-th centered nonagonal number and is equal to the sum of the first [math]\displaystyle{ 2^\frac{p-1}{2} }[/math] odd cubes (odd cubes up to the cube of [math]\displaystyle{ 2^\frac{p+1}{2}-1 }[/math]):

[math]\displaystyle{ \begin{alignat}{3} 6 &= 2^1(2^2 - 1) &&= 1 + 2 + 3, \\[8pt] 28 &= 2^2(2^3 - 1) &&= 1 + 2 + 3 + 4 + 5 + 6 + 7 \\ & &&= 1^3 + 3^3 \\[8pt] 496 &= 2^4(2^5 - 1) &&= 1 + 2 + 3 + \cdots + 29 + 30 + 31 \\ & &&= 1^3 + 3^3 + 5^3 + 7^3 \\[8pt] 8128 &= 2^6(2^7 - 1) &&= 1 + 2 + 3 + \cdots + 125 + 126 + 127 \\ & &&= 1^3 + 3^3 + 5^3 + 7^3 + 9^3 + 11^3 + 13^3 + 15^3 \\[8pt] 33550336 &= 2^{12}(2^{13} - 1) &&= 1 + 2 + 3 + \cdots + 8189 + 8190 + 8191 \\ & &&= 1^3 + 3^3 + 5^3 + \cdots + 123^3 + 125^3 + 127^3 \end{alignat} }[/math]

Even perfect numbers (except 6) are of the form [math]\displaystyle{ T_{2^p - 1} = 1 + \frac{(2^p - 2) \times (2^p + 1)}{2} = 1 + 9 \times T_{(2^p - 2)/3} }[/math]

with each resulting triangular number T₇ = 28, T₃₁ = 496, T₁₂₇ = 8128 (after subtracting 1 from the perfect number and dividing the result by 9) ending in 3 or 5, the sequence starting with T₂ = 3, T₁₀ = 55, T₄₂ = 903, T₂₇₃₀ = 3727815, ... It follows that by adding the digits of any even perfect number (except 6), then adding the digits of the resulting number, and repeating this process until a single digit (called the digital root) is obtained, always produces the number 1. For example, the digital root of 8128 is 1, because 8 + 1 + 2 + 8 = 19, 1 + 9 = 10, and 1 + 0 = 1. This works with all perfect numbers [math]\displaystyle{ 2^{p-1}(2^p-1) }[/math] with odd prime p and, in fact, with all numbers of the form [math]\displaystyle{ 2^{m-1}(2^m-1) }[/math] for odd integer (not necessarily prime) m.

Owing to their form, [math]\displaystyle{ 2^{p-1}(2^p-1), }[/math] every even perfect number is represented in binary form as p ones followed by p − 1 zeros; for example:

[math]\displaystyle{ \begin{array}{rcl} 6_{10} =& 2^2 + 2^1 &= 110_2 \\ 28_{10} =& 2^4 + 2^3 + 2^2 &= 11100_2 \\ 496_{10} =& 2^8 + 2^7 + 2^6 + 2^5 + 2^4 &= 111110000_2 \\ 8128_{10} =& \!\! 2^{12} + 2^{11} + 2^{10} + 2^9 + 2^8 + 2^7 + 2^6 \!\! &= 1111111000000_2 \end{array} }[/math]

Thus every even perfect number is a pernicious number.

Every even perfect number is also a practical number (cf. Related concepts).

Odd perfect numbers

Unsolved problem in mathematics: Are there any odd perfect numbers? (more unsolved problems in mathematics)

It is unknown whether any odd perfect numbers exist, though various results have been obtained. In 1496, Jacques Lefèvre stated that Euclid's rule gives all perfect numbers, thus implying that no odd perfect number exists. Euler stated: "Whether ... there are any odd perfect numbers is a most difficult question". More recently, Carl Pomerance has presented a heuristic argument suggesting that indeed no odd perfect number should exist. All perfect numbers are also harmonic divisor numbers, and it has been conjectured as well that there are no odd harmonic divisor numbers other than 1. Many of the properties proved about odd perfect numbers also apply to Descartes numbers, and Pace Nielsen has suggested that sufficient study of those numbers may lead to a proof that no odd perfect numbers exist.

Any odd perfect number N must satisfy the following conditions:

• N > 10¹⁵⁰⁰.
• N is not divisible by 105.
• N is of the form N ≡ 1 (mod 12) or N ≡ 117 (mod 468) or N ≡ 81 (mod 324).
• N is of the form

[math]\displaystyle{ N=q^{\alpha} p_1^{2e_1} \cdots p_k^{2e_k}, }[/math]

where:

• q, p₁, ..., p_k are distinct odd primes (Euler).
• q ≡ α ≡ 1 (mod 4) (Euler).
• The smallest prime factor of N is at most [math]\displaystyle{ \frac{k-1}{2}. }[/math]
• Either q^α > 10⁶², or p_j^2e_j  > 10⁶² for some j.
• [math]\displaystyle{ N \lt 2^{(4^{k+1}-2^{k+1})} }[/math]
• [math]\displaystyle{ \alpha + 2e_1 + 2e_2 + 2e_3 + \cdots + 2e_k \geq \frac{99k-224}{37} }[/math].
• [math]\displaystyle{ qp_1p_2p_3 \cdots p_k \lt 2N^{\frac{17}{26}} }[/math].

• The largest prime factor of N is greater than 10⁸ and less than [math]\displaystyle{ \sqrt[3]{3N}. }[/math]
• The second largest prime factor is greater than 10⁴, and is less than [math]\displaystyle{ \sqrt[5]{2N} }[/math].
• The third largest prime factor is greater than 100, and less than [math]\displaystyle{ \sqrt[6]{2N}. }[/math]
• N has at least 101 prime factors and at least 10 distinct prime factors. If 3 is not one of the factors of N, then N has at least 12 distinct prime factors.

Furthermore, several minor results are known about the exponents e₁, ..., e_k.

• Not all e_i ≡ 1 (mod 3).
• Not all e_i ≡ 2 (mod 5).
• If all e_i ≡ 1 (mod 3) or 2 (mod 5), then the smallest prime factor of N must lie between 10⁸ and 10¹⁰⁰⁰.
• More generally, if all 2e_i+1 have a prime factor in a given finite set S, then the smallest prime factor of N must be smaller than an effectively computable constant depending only on S.
• If (e₁, ..., e_k) =  (1, ..., 1, 2, ..., 2) with t ones and u twos, then [math]\displaystyle{ (t-1)/4 \leq u \leq 2t+\sqrt{\alpha} }[/math].
• (e₁, ..., e_k) ≠ (1, ..., 1, 3), (1, ..., 1, 5), (1, ..., 1, 6).
• If e₁ = ... = e_k = e, then
  • e cannot be 3, 5, 24, 6, 8, 11, 14 or 18.
  • [math]\displaystyle{ k\leq 2e^2+8e+2 }[/math] and [math]\displaystyle{ N\lt 2^{4^{2e^2 + 8e+3}} }[/math].

In 1888, Sylvester stated:

... a prolonged meditation on the subject has satisfied me that the existence of any one such [odd perfect number]—its escape, so to say, from the complex web of conditions which hem it in on all sides—would be little short of a miracle.

Minor results

All even perfect numbers have a very precise form; odd perfect numbers either do not exist or are rare. There are a number of results on perfect numbers that are actually quite easy to prove but nevertheless superficially impressive; some of them also come under Richard Guy's strong law of small numbers:

• The only even perfect number of the form n³ + 1 is 28 (Makowski 1962).
• 28 is also the only even perfect number that is a sum of two positive cubes of integers (Gallardo 2010).
• The reciprocals of the divisors of a perfect number N must add up to 2 (to get this, take the definition of a perfect number, [math]\displaystyle{ \sigma_1(n) = 2n }[/math], and divide both sides by n):
  • For 6, we have [math]\displaystyle{ 1/6 + 1/3 + 1/2 + 1/1 = 2 }[/math];
  • For 28, we have [math]\displaystyle{ 1/28 + 1/14 + 1/7 + 1/4 + 1/2 + 1/1 = 2 }[/math], etc.
• The number of divisors of a perfect number (whether even or odd) must be even, because N cannot be a perfect square.
  • From these two results it follows that every perfect number is an Ore's harmonic number.
• The even perfect numbers are not trapezoidal numbers; that is, they cannot be represented as the difference of two positive non-consecutive triangular numbers. There are only three types of non-trapezoidal numbers: even perfect numbers, powers of two, and the numbers of the form [math]\displaystyle{ 2^{n-1}(2^n+1) }[/math] formed as the product of a Fermat prime [math]\displaystyle{ 2^n+1 }[/math] with a power of two in a similar way to the construction of even perfect numbers from Mersenne primes.
• The number of perfect numbers less than n is less than [math]\displaystyle{ c\sqrt{n} }[/math], where c > 0 is a constant. In fact it is [math]\displaystyle{ o(\sqrt{n}) }[/math], using little-o notation.
• Every even perfect number ends in 6 or 28, base ten; and, with the only exception of 6, ends in 1 in base 9. Therefore, in particular the digital root of every even perfect number other than 6 is 1.
• The only square-free perfect number is 6.

Related concepts

Euler diagram of abundant, primitive abundant, highly abundant, superabundant, colossally abundant, highly composite, superior highly composite, weird and perfect numbers under 100 in relation to deficient and composite numbers

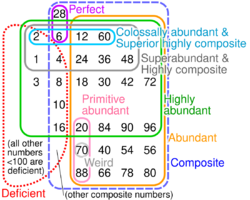
The sum of proper divisors gives various other kinds of numbers. Numbers where the sum is less than the number itself are called deficient, and where it is greater than the number, abundant. These terms, together with perfect itself, come from Greek numerology. A pair of numbers which are the sum of each other's proper divisors are called amicable, and larger cycles of numbers are called sociable. A positive integer such that every smaller positive integer is a sum of distinct divisors of it is a practical number.

By definition, a perfect number is a fixed point of the restricted divisor function s(n) = σ(n) − n, and the aliquot sequence associated with a perfect number is a constant sequence. All perfect numbers are also [math]\displaystyle{ \mathcal{S} }[/math]-perfect numbers, or Granville numbers.

A semiperfect number is a natural number that is equal to the sum of all or some of its proper divisors. A semiperfect number that is equal to the sum of all its proper divisors is a perfect number. Most abundant numbers are also semiperfect; abundant numbers which are not semiperfect are called weird numbers.

See also

• Hyperperfect number
• Leinster group
• List of Mersenne primes and perfect numbers
• Multiply perfect number
• Superperfect numbers
• Unitary perfect number
• Harmonic divisor number

References

Sources

• Euclid, Elements, Book IX, Proposition 36. See D.E. Joyce's website for a translation and discussion of this proposition and its proof.
• Kanold, H.-J. (1941). "Untersuchungen über ungerade vollkommene Zahlen". Journal für die Reine und Angewandte Mathematik 1941 (183): 98–109. doi:10.1515/crll.1941.183.98. 
• Steuerwald, R.. "Verschärfung einer notwendigen Bedingung für die Existenz einer ungeraden vollkommenen Zahl". S.-B. Bayer. Akad. Wiss. 1937: 69–72. 

Further reading

• Nankar, M.L.: "History of perfect numbers," Ganita Bharati 1, no. 1–2 (1979), 7–8.
• Hagis, P. (1973). "A Lower Bound for the set of odd Perfect Prime Numbers". Mathematics of Computation 27 (124): 951–953. doi:10.2307/2005530. 
• Riele, H.J.J. "Perfect Numbers and Aliquot Sequences" in H.W. Lenstra and R. Tijdeman (eds.): Computational Methods in Number Theory, Vol. 154, Amsterdam, 1982, pp. 141–157.
• Riesel, H. Prime Numbers and Computer Methods for Factorisation, Birkhauser, 1985.
• Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. pp. 15–98. ISBN 1-4020-2546-7. https://archive.org/details/handbooknumberth02sand. 

External links

• Hazewinkel, Michiel, ed. (2001), "Perfect number", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/p072090 
• David Moews: Perfect, amicable and sociable numbers
• Perfect numbers – History and Theory
• Weisstein, Eric W.. "Perfect Number". http://mathworld.wolfram.com/PerfectNumber.html. 
• OEIS sequence A000396 (Perfect numbers)
• OddPerfect.org A projected distributed computing project to search for odd perfect numbers.
• Great Internet Mersenne Prime Search (GIMPS)
• Perfect Numbers, math forum at Drexel.
• Grimes, James. "8128: Perfect Numbers". Numberphile. Brady Haran. http://www.numberphile.com/videos/8128.html.