Almost perfect number

Short description: Class of natural number

Demonstration, with Cuisenaire rods, that the number 8 is almost perfect, and deficient.

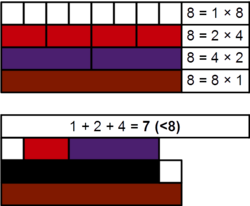
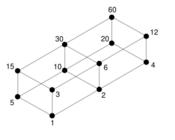
In mathematics, an almost perfect number (sometimes also called slightly defective or least deficient number) is a natural number n such that the sum of all divisors of n (the sum-of-divisors function σ(n)) is equal to 2n − 1, the sum of all proper divisors of n, s(n) = σ(n) − n, then being equal to n − 1. The only known almost perfect numbers are powers of 2 with non-negative exponents (sequence A000079 in the OEIS). Therefore the only known odd almost perfect number is 2⁰ = 1, and the only known even almost perfect numbers are those of the form 2^k for some positive integer k; however, it has not been shown that all almost perfect numbers are of this form. It is known that an odd almost perfect number greater than 1 would have at least six prime factors.

If m is an odd almost perfect number then m(2m − 1) is a Descartes number. Moreover if a and b are positive odd integers such that [math]\displaystyle{ b+3\lt a\lt \sqrt{m/2} }[/math] and such that 4m − a and 4m + b are both primes, then m(4m − a)(4m + b) would be an odd weird number.

See also

• Perfect number
• Quasiperfect number

Further reading

• Guy, R. K. (1994). "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers". Unsolved Problems in Number Theory (2nd ed.). New York: Springer-Verlag. pp. 16, 45–53. 
• Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. p. 110. ISBN 1-4020-4215-9. 
• Sándor, Jozsef; Crstici, Borislav, eds (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. pp. 37–38. ISBN 1-4020-2546-7. 
• Singh, S. (1997). Fermat's Enigma: The Epic Quest to Solve the World's Greatest Mathematical Problem. New York: Walker. p. 13. ISBN 9780802713315. https://archive.org/details/fermatsenigmaepi00sing_0. 

External links

• Weisstein, Eric W.. "Almost perfect number". http://mathworld.wolfram.com/AlmostPerfectNumber.html.