Unitary perfect number

Short description: Integer which is the sum of its positive proper unitary divisors, not including itself

Unsolved problem in mathematics: Are there infinitely many unitary perfect numbers? (more unsolved problems in mathematics)

A unitary perfect number is an integer which is the sum of its positive proper unitary divisors, not including the number itself (a divisor d of a number n is a unitary divisor if d and n/d share no common factors). Some perfect numbers are not unitary perfect numbers, and some unitary perfect numbers are not ordinary perfect numbers.

Known examples

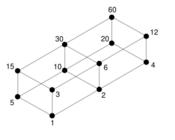
The number 60 is a unitary perfect number because 1, 3, 4, 5, 12, 15, and 20 are its proper unitary divisors, and 1 + 3 + 4 + 5 + 12 + 15 + 20 = 60. The first five, and only known, unitary perfect numbers are [math]\displaystyle{ 6 = 2 \times 3 }[/math], [math]\displaystyle{ 60 = 2^2 \times 3 \times 5 }[/math], [math]\displaystyle{ 90 = 2 \times 3^2 \times 5 }[/math], [math]\displaystyle{ 87360 = 2^6 \times 3 \times 5 \times 7 \times 13 }[/math], and [math]\displaystyle{ 146361946186458562560000 = 2^{18} \times 3 \times 5^4 \times 7 \times 11 \times 13 \times 19 \times 37 \times 79 \times 109 \times 157 \times 313 }[/math] (sequence A002827 in the OEIS). The respective sums of their proper unitary divisors are as follows:

• 6 = 1 + 2 + 3
• 60 = 1 + 3 + 4 + 5 + 12 + 15 + 20
• 90 = 1 + 2 + 5 + 9 + 10 + 18 + 45
• 87360 = 1 + 3 + 5 + 7 + 13 + 15 + 21 + 35 + 39 + 64 + 65 + 91 + 105 + 192 + 195 + 273 + 320 + 448 + 455 + 832 + 960 + 1344 + 1365 + 2240 + 2496 + 4160 + 5824 + 6720 + 12480 + 17472 + 29120
• 146361946186458562560000 = 1 + 3 + 7 + 11 + ... + 13305631471496232960000 + 20908849455208366080000 + 48787315395486187520000 (4095 divisors in the sum)

Properties

There are no odd unitary perfect numbers. This follows since 2^d*(n) divides the sum of the unitary divisors of an odd number n, where d*(n) is the number of distinct prime factors of n. One gets this because the sum of all the unitary divisors is a multiplicative function and one has that the sum of the unitary divisors of a prime power p^a is p^a + 1 which is even for all odd primes p. Therefore, an odd unitary perfect number must have only one distinct prime factor, and it is not hard to show that a power of prime cannot be a unitary perfect number, since there are not enough divisors.

It is not known whether or not there are infinitely many unitary perfect numbers, or indeed whether there are any further examples beyond the five already known. A sixth such number would have at least nine odd prime factors.

References

• Richard K. Guy (2004). Unsolved Problems in Number Theory. Springer-Verlag. pp. 84–86. ISBN 0-387-20860-7.  Section B3.
• Paulo Ribenboim (2000). My Numbers, My Friends: Popular Lectures on Number Theory. Springer-Verlag. p. 352. ISBN 0-387-98911-0. 
• Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. ISBN 1-4020-4215-9. 
• Sándor, Jozsef; Crstici, Borislav (2004). Handbook of number theory II. Dordrecht: Kluwer Academic. ISBN 1-4020-2546-7.