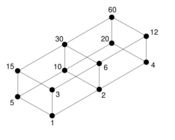
Highly composite number

Short description: Positive integer with more divisors than any smaller positive integer

Demonstration, with Cuisenaire rods, of the first four: 1, 2, 4, 6

A highly composite number is a positive integer with more divisors than any smaller positive integer has. A related concept is that of a largely composite number, a positive integer which has at least as many divisors as any smaller positive integer. The name can be somewhat misleading, as the first two highly composite numbers (1 and 2) are not actually composite numbers; however, all further terms are.

Ramanujan wrote a paper on highly composite numbers in 1915.

The mathematician Jean-Pierre Kahane suggested that Plato must have known about highly composite numbers as he deliberately chose such a number, 5040 (= 7!), as the ideal number of citizens in a city.

Examples

The initial or smallest 41 highly composite numbers are listed in the table below (sequence A002182 in the OEIS). The number of divisors is given in the column labeled d(n). Asterisks indicate superior highly composite numbers.

Order	HCN n	prime factorization	prime exponents	number of prime factors	d(n)	primorial factorization
1	1			0	1
2	2*	[math]\displaystyle{ 2 }[/math]	1	1	2	[math]\displaystyle{ 2 }[/math]
3	4	[math]\displaystyle{ 2^2 }[/math]	2	2	3	[math]\displaystyle{ 2^2 }[/math]
4	6*	[math]\displaystyle{ 2\cdot 3 }[/math]	1,1	2	4	[math]\displaystyle{ 6 }[/math]
5	12*	[math]\displaystyle{ 2^2\cdot 3 }[/math]	2,1	3	6	[math]\displaystyle{ 2\cdot 6 }[/math]
6	24	[math]\displaystyle{ 2^3\cdot 3 }[/math]	3,1	4	8	[math]\displaystyle{ 2^2\cdot 6 }[/math]
7	36	[math]\displaystyle{ 2^2\cdot 3^2 }[/math]	2,2	4	9	[math]\displaystyle{ 6^2 }[/math]
8	48	[math]\displaystyle{ 2^4\cdot 3 }[/math]	4,1	5	10	[math]\displaystyle{ 2^3\cdot 6 }[/math]
9	60*	[math]\displaystyle{ 2^2\cdot 3\cdot 5 }[/math]	2,1,1	4	12	[math]\displaystyle{ 2\cdot 30 }[/math]
10	120*	[math]\displaystyle{ 2^3\cdot 3\cdot 5 }[/math]	3,1,1	5	16	[math]\displaystyle{ 2^2\cdot 30 }[/math]
11	180	[math]\displaystyle{ 2^2\cdot 3^2\cdot 5 }[/math]	2,2,1	5	18	[math]\displaystyle{ 6\cdot 30 }[/math]
12	240	[math]\displaystyle{ 2^4\cdot 3\cdot 5 }[/math]	4,1,1	6	20	[math]\displaystyle{ 2^3\cdot 30 }[/math]
13	360*	[math]\displaystyle{ 2^3\cdot 3^2\cdot 5 }[/math]	3,2,1	6	24	[math]\displaystyle{ 2\cdot 6\cdot 30 }[/math]
14	720	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5 }[/math]	4,2,1	7	30	[math]\displaystyle{ 2^2\cdot 6\cdot 30 }[/math]
15	840	[math]\displaystyle{ 2^3\cdot 3\cdot 5\cdot 7 }[/math]	3,1,1,1	6	32	[math]\displaystyle{ 2^2\cdot 210 }[/math]
16	1260	[math]\displaystyle{ 2^2\cdot 3^2\cdot 5\cdot 7 }[/math]	2,2,1,1	6	36	[math]\displaystyle{ 6\cdot 210 }[/math]
17	1680	[math]\displaystyle{ 2^4\cdot 3\cdot 5\cdot 7 }[/math]	4,1,1,1	7	40	[math]\displaystyle{ 2^3\cdot 210 }[/math]
18	2520*	[math]\displaystyle{ 2^3\cdot 3^2\cdot 5\cdot 7 }[/math]	3,2,1,1	7	48	[math]\displaystyle{ 2\cdot 6\cdot 210 }[/math]
19	5040*	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5\cdot 7 }[/math]	4,2,1,1	8	60	[math]\displaystyle{ 2^2\cdot 6\cdot 210 }[/math]
20	7560	[math]\displaystyle{ 2^3\cdot 3^3\cdot 5\cdot 7 }[/math]	3,3,1,1	8	64	[math]\displaystyle{ 6^2\cdot 210 }[/math]
21	10080	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5\cdot 7 }[/math]	5,2,1,1	9	72	[math]\displaystyle{ 2^3\cdot 6\cdot 210 }[/math]
22	15120	[math]\displaystyle{ 2^4\cdot 3^3\cdot 5\cdot 7 }[/math]	4,3,1,1	9	80	[math]\displaystyle{ 2\cdot 6^2\cdot 210 }[/math]
23	20160	[math]\displaystyle{ 2^6\cdot 3^2\cdot 5\cdot 7 }[/math]	6,2,1,1	10	84	[math]\displaystyle{ 2^4\cdot 6\cdot 210 }[/math]
24	25200	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5^2\cdot 7 }[/math]	4,2,2,1	9	90	[math]\displaystyle{ 2^2\cdot 30\cdot 210 }[/math]
25	27720	[math]\displaystyle{ 2^3\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	3,2,1,1,1	8	96	[math]\displaystyle{ 2\cdot 6\cdot 2310 }[/math]
26	45360	[math]\displaystyle{ 2^4\cdot 3^4\cdot 5\cdot 7 }[/math]	4,4,1,1	10	100	[math]\displaystyle{ 6^3\cdot 210 }[/math]
27	50400	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5^2\cdot 7 }[/math]	5,2,2,1	10	108	[math]\displaystyle{ 2^3\cdot 30\cdot 210 }[/math]
28	55440*	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	4,2,1,1,1	9	120	[math]\displaystyle{ 2^2\cdot 6\cdot 2310 }[/math]
29	83160	[math]\displaystyle{ 2^3\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	3,3,1,1,1	9	128	[math]\displaystyle{ 6^2\cdot 2310 }[/math]
30	110880	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	5,2,1,1,1	10	144	[math]\displaystyle{ 2^3\cdot 6\cdot 2310 }[/math]
31	166320	[math]\displaystyle{ 2^4\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	4,3,1,1,1	10	160	[math]\displaystyle{ 2\cdot 6^2\cdot 2310 }[/math]
32	221760	[math]\displaystyle{ 2^6\cdot 3^2\cdot 5\cdot 7\cdot 11 }[/math]	6,2,1,1,1	11	168	[math]\displaystyle{ 2^4\cdot 6\cdot 2310 }[/math]
33	277200	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5^2\cdot 7\cdot 11 }[/math]	4,2,2,1,1	10	180	[math]\displaystyle{ 2^2\cdot 30\cdot 2310 }[/math]
34	332640	[math]\displaystyle{ 2^5\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	5,3,1,1,1	11	192	[math]\displaystyle{ 2^2\cdot 6^2\cdot 2310 }[/math]
35	498960	[math]\displaystyle{ 2^4\cdot 3^4\cdot 5\cdot 7\cdot 11 }[/math]	4,4,1,1,1	11	200	[math]\displaystyle{ 6^3\cdot 2310 }[/math]
36	554400	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5^2\cdot 7\cdot 11 }[/math]	5,2,2,1,1	11	216	[math]\displaystyle{ 2^3\cdot 30\cdot 2310 }[/math]
37	665280	[math]\displaystyle{ 2^6\cdot 3^3\cdot 5\cdot 7\cdot 11 }[/math]	6,3,1,1,1	12	224	[math]\displaystyle{ 2^3\cdot 6^2\cdot 2310 }[/math]
38	720720*	[math]\displaystyle{ 2^4\cdot 3^2\cdot 5\cdot 7\cdot 11\cdot 13 }[/math]	4,2,1,1,1,1	10	240	[math]\displaystyle{ 2^2\cdot 6\cdot 30030 }[/math]
39	1081080	[math]\displaystyle{ 2^3\cdot 3^3\cdot 5\cdot 7\cdot 11\cdot 13 }[/math]	3,3,1,1,1,1	10	256	[math]\displaystyle{ 6^2\cdot 30030 }[/math]
40	1441440*	[math]\displaystyle{ 2^5\cdot 3^2\cdot 5\cdot 7\cdot 11\cdot 13 }[/math]	5,2,1,1,1,1	11	288	[math]\displaystyle{ 2^3\cdot 6\cdot 30030 }[/math]
41	2162160	[math]\displaystyle{ 2^4\cdot 3^3\cdot 5\cdot 7\cdot 11\cdot 13 }[/math]	4,3,1,1,1,1	11	320	[math]\displaystyle{ 2\cdot 6^2\cdot 30030 }[/math]

The divisors of the first 19 highly composite numbers are shown below.

n	d(n)	Divisors of n
1	1	1
2	2	1, 2
4	3	1, 2, 4
6	4	1, 2, 3, 6
12	6	1, 2, 3, 4, 6, 12
24	8	1, 2, 3, 4, 6, 8, 12, 24
36	9	1, 2, 3, 4, 6, 9, 12, 18, 36
48	10	1, 2, 3, 4, 6, 8, 12, 16, 24, 48
60	12	1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
120	16	1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
180	18	1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180
240	20	1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240
360	24	1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360
720	30	1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360, 720
840	32	1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70, 84, 105, 120, 140, 168, 210, 280, 420, 840
1260	36	1, 2, 3, 4, 5, 6, 7, 9, 10, 12, 14, 15, 18, 20, 21, 28, 30, 35, 36, 42, 45, 60, 63, 70, 84, 90, 105, 126, 140, 180, 210, 252, 315, 420, 630, 1260
1680	40	1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 16, 20, 21, 24, 28, 30, 35, 40, 42, 48, 56, 60, 70, 80, 84, 105, 112, 120, 140, 168, 210, 240, 280, 336, 420, 560, 840, 1680
2520	48	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 21, 24, 28, 30, 35, 36, 40, 42, 45, 56, 60, 63, 70, 72, 84, 90, 105, 120, 126, 140, 168, 180, 210, 252, 280, 315, 360, 420, 504, 630, 840, 1260, 2520
5040	60	1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 28, 30, 35, 36, 40, 42, 45, 48, 56, 60, 63, 70, 72, 80, 84, 90, 105, 112, 120, 126, 140, 144, 168, 180, 210, 240, 252, 280, 315, 336, 360, 420, 504, 560, 630, 720, 840, 1008, 1260, 1680, 2520, 5040

The table below shows all 72 divisors of 10080 by writing it as a product of two numbers in 36 different ways.

The highly composite number: 10080 10080 = (2 × 2 × 2 × 2 × 2)  ×  (3 × 3)  ×  5  ×  7
1 × 10080	2 × 5040	3 × 3360	4 × 2520	5 × 2016	6 × 1680
7 × 1440	8 × 1260	9 × 1120	10 × 1008	12 × 840	14 × 720
15 × 672	16 × 630	18 × 560	20 × 504	21 × 480	24 × 420
28 × 360	30 × 336	32 × 315	35 × 288	36 × 280	40 × 252
42 × 240	45 × 224	48 × 210	56 × 180	60 × 168	63 × 160
70 × 144	72 × 140	80 × 126	84 × 120	90 × 112	96 × 105
Note:  Numbers in bold are themselves highly composite numbers. Only the twentieth highly composite number 7560 (= 3 × 2520) is absent. 10080 is a so-called 7-smooth number (sequence A002473 in the OEIS).

The 15,000th highly composite number can be found on Achim Flammenkamp's website. It is the product of 230 primes:

[math]\displaystyle{ a_0^{14} a_1^9 a_2^6 a_3^4 a_4^4 a_5^3 a_6^3 a_7^3 a_8^2 a_9^2 a_{10}^2 a_{11}^2 a_{12}^2 a_{13}^2 a_{14}^2 a_{15}^2 a_{16}^2 a_{17}^2 a_{18}^{2} a_{19} a_{20} a_{21}\cdots a_{229}, }[/math]

where [math]\displaystyle{ a_n }[/math] is the [math]\displaystyle{ n }[/math]th successive prime number, and all omitted terms (a₂₂ to a₂₂₈) are factors with exponent equal to one (i.e. the number is [math]\displaystyle{ 2^{14} \times 3^{9} \times 5^6 \times \cdots \times 1451 }[/math]). More concisely, it is the product of seven distinct primorials:

[math]\displaystyle{ b_0^5 b_1^3 b_2^2 b_4 b_7 b_{18} b_{229}, }[/math]

where [math]\displaystyle{ b_n }[/math] is the primorial [math]\displaystyle{ a_0a_1\cdots a_n }[/math].

Plot of the number of divisors of integers from 1 to 1000. Highly composite numbers are labelled in bold and superior highly composite numbers are starred. In the SVG file, hover over a bar to see its statistics.

Prime factorization

Roughly speaking, for a number to be highly composite it has to have prime factors as small as possible, but not too many of the same. By the fundamental theorem of arithmetic, every positive integer n has a unique prime factorization:

[math]\displaystyle{ n = p_1^{c_1} \times p_2^{c_2} \times \cdots \times p_k^{c_k}\qquad (1) }[/math]

where [math]\displaystyle{ p_1 \lt p_2 \lt \cdots \lt p_k }[/math] are prime, and the exponents [math]\displaystyle{ c_i }[/math] are positive integers.

Any factor of n must have the same or lesser multiplicity in each prime:

[math]\displaystyle{ p_1^{d_1} \times p_2^{d_2} \times \cdots \times p_k^{d_k}, 0 \leq d_i \leq c_i, 0 \lt i \leq k }[/math]

So the number of divisors of n is:

[math]\displaystyle{ d(n) = (c_1 + 1) \times (c_2 + 1) \times \cdots \times (c_k + 1).\qquad (2) }[/math]

Hence, for a highly composite number n,

• the k given prime numbers p_i must be precisely the first k prime numbers (2, 3, 5, ...); if not, we could replace one of the given primes by a smaller prime, and thus obtain a smaller number than n with the same number of divisors (for instance 10 = 2 × 5 may be replaced with 6 = 2 × 3; both have four divisors);
• the sequence of exponents must be non-increasing, that is [math]\displaystyle{ c_1 \geq c_2 \geq \cdots \geq c_k }[/math]; otherwise, by exchanging two exponents we would again get a smaller number than n with the same number of divisors (for instance 18 = 2¹ × 3² may be replaced with 12 = 2² × 3¹; both have six divisors).

Also, except in two special cases n = 4 and n = 36, the last exponent c_k must equal 1. It means that 1, 4, and 36 are the only square highly composite numbers. Saying that the sequence of exponents is non-increasing is equivalent to saying that a highly composite number is a product of primorials or, alternatively, the smallest number for its prime signature.

Note that although the above described conditions are necessary, they are not sufficient for a number to be highly composite. For example, 96 = 2⁵ × 3 satisfies the above conditions and has 12 divisors but is not highly composite since there is a smaller number 60 which has the same number of divisors.

Asymptotic growth and density

If Q(x) denotes the number of highly composite numbers less than or equal to x, then there are two constants a and b, both greater than 1, such that

[math]\displaystyle{ (\log x)^a \le Q(x) \le (\log x)^b \, . }[/math]

The first part of the inequality was proved by Paul Erdős in 1944 and the second part by Jean-Louis Nicolas in 1988. We have

[math]\displaystyle{ 1.13862 \lt \liminf \frac{\log Q(x)}{\log\log x} \le 1.44 \ }[/math]

and

[math]\displaystyle{ \limsup \frac{\log Q(x)}{\log\log x} \le 1.71 \ . }[/math]

Related sequences

Euler diagram of abundant, primitive abundant, highly abundant, superabundant, colossally abundant, highly composite, superior highly composite, weird and perfect numbers under 100 in relation to deficient and composite numbers

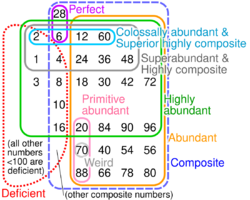
Highly composite numbers higher than 6 are also abundant numbers. One need only look at the three largest proper divisors of a particular highly composite number to ascertain this fact. It is false that all highly composite numbers are also Harshad numbers in base 10. The first HCN that is not a Harshad number is 245,044,800, which has a digit sum of 27, but 27 does not divide evenly into 245,044,800.

10 of the first 38 highly composite numbers are superior highly composite numbers. The sequence of highly composite numbers (sequence A002182 in the OEIS) is a subset of the sequence of smallest numbers k with exactly n divisors (sequence A005179 in the OEIS).

Highly composite numbers whose number of divisors is also a highly composite number are for n = 1, 2, 6, 12, 60, 360, 1260, 2520, 5040, 55440, 277200, 720720, 3603600, 61261200, 2205403200, 293318625600, 6746328388800, 195643523275200 (sequence A189394 in the OEIS). It is extremely likely that this sequence is complete.

A positive integer n is a largely composite number if d(n) ≥ d(m) for all m ≤ n. The counting function Q_L(x) of largely composite numbers satisfies

[math]\displaystyle{ (\log x)^c \le \log Q_L(x) \le (\log x)^d \ }[/math]

for positive c,d with [math]\displaystyle{ 0.2 \le c \le d \le 0.5 }[/math].

Because the prime factorization of a highly composite number uses all of the first k primes, every highly composite number must be a practical number. Due to their ease of use in calculations involving fractions, many of these numbers are used in traditional systems of measurement and engineering designs.

See also

• Superior highly composite number
• Highly totient number
• Table of divisors
• Euler's totient function
• Round number
• Smooth number

References

• Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. pp. 45–46. ISBN 1-4020-4215-9. 
• "On highly composite numbers". Journal of the London Mathematical Society. Second Series 19 (75_Part_3): 130–133. 1944. doi:10.1112/jlms/19.75_part_3.130. https://www.renyi.hu/~p_erdos/1944-04.pdf. 
• "On highly composite and similar numbers". Transactions of the American Mathematical Society 56 (3): 448–469. 1944. doi:10.2307/1990319. https://www.renyi.hu/~p_erdos/1944-03.pdf. 
• "Highly composite numbers". Ramanujan Journal 1 (2): 119–153. 1997. doi:10.1023/A:1009764017495. http://math.univ-lyon1.fr/~nicolas/ramanujanNR.pdf.  Annotated and with a foreword by Jean-Louis Nicolas and Guy Robin.

External links

• Weisstein, Eric W.. "Highly Composite Number". http://mathworld.wolfram.com/HighlyCompositeNumber.html. 
• Algorithm for computing Highly Composite Numbers
• First 10000 Highly Composite Numbers as factors
• Achim Flammenkamp, First 779674 HCN with sigma,tau,factors
• Online Highly Composite Numbers Calculator

• 5040 and other Anti-Prime Numbers - Dr. James Grime by Dr. James Grime for Numberphile