Polydivisible number

From HandWiki
Short description: A number whose first n digits is a multiple of n


In mathematics a polydivisible number (or magic number) is a number in a given number base with digits abcde... that has the following properties:[1]

  1. Its first digit a is not 0.
  2. The number formed by its first two digits ab is a multiple of 2.
  3. The number formed by its first three digits abc is a multiple of 3.
  4. The number formed by its first four digits abcd is a multiple of 4.
  5. etc.

Definition

Let [math]\displaystyle{ n }[/math] be a positive integer, and let [math]\displaystyle{ k = \lfloor \log_{b}{n} \rfloor + 1 }[/math] be the number of digits in n written in base b. The number n is a polydivisible number if for all [math]\displaystyle{ 1 \leq i \leq k }[/math],

[math]\displaystyle{ \left\lfloor\frac{n}{b^{k - i}}\right\rfloor \equiv 0 \pmod i }[/math].
Example

For example, 10801 is a seven-digit polydivisible number in base 4, as

[math]\displaystyle{ \left\lfloor\frac{10801}{4^{7 - 1}}\right\rfloor = \left\lfloor\frac{10801}{4096}\right\rfloor = 2 \equiv 0 \pmod 1, }[/math]
[math]\displaystyle{ \left\lfloor\frac{10801}{4^{7 - 2}}\right\rfloor = \left\lfloor\frac{10801}{1024}\right\rfloor = 10 \equiv 0 \pmod 2, }[/math]
[math]\displaystyle{ \left\lfloor\frac{10801}{4^{7 - 3}}\right\rfloor = \left\lfloor\frac{10801}{256}\right\rfloor = 42 \equiv 0 \pmod 3, }[/math]
[math]\displaystyle{ \left\lfloor\frac{10801}{4^{7 - 4}}\right\rfloor = \left\lfloor\frac{10801}{64}\right\rfloor = 168 \equiv 0 \pmod 4, }[/math]
[math]\displaystyle{ \left\lfloor\frac{10801}{4^{7 - 5}}\right\rfloor = \left\lfloor\frac{10801}{16}\right\rfloor = 675 \equiv 0 \pmod 5, }[/math]
[math]\displaystyle{ \left\lfloor\frac{10801}{4^{7 - 6}}\right\rfloor = \left\lfloor\frac{10801}{4}\right\rfloor = 2700 \equiv 0 \pmod 6, }[/math]
[math]\displaystyle{ \left\lfloor\frac{10801}{4^{7 - 7}}\right\rfloor = \left\lfloor\frac{10801}{1}\right\rfloor = 10801 \equiv 0 \pmod 7. }[/math]

Enumeration

For any given base [math]\displaystyle{ b }[/math], there are only a finite number of polydivisible numbers.

Maximum polydivisible number

The following table lists maximum polydivisible numbers for some bases b, where A−Z represent digit values 10 to 35.

Base [math]\displaystyle{ b }[/math] Maximum polydivisible number (OEIS: A109032) Number of base-b digits (OEIS: A109783)
2 102 2
3 20 02203 6
4 222 03014 7
5 40220 422005 10
10 36085 28850 36840 07860 36725[2][3][4] 25
12 6068 903468 50BA68 00B036 20646412 28

Estimate for Fb(n) and Σ(b)

Graph of number of [math]\displaystyle{ n }[/math]-digit polydivisible numbers in base 10 [math]\displaystyle{ F_{10}(n) }[/math] vs estimate of [math]\displaystyle{ F_{10}(n) }[/math]

Let [math]\displaystyle{ n }[/math] be the number of digits. The function [math]\displaystyle{ F_b(n) }[/math] determines the number of polydivisible numbers that has [math]\displaystyle{ n }[/math] digits in base [math]\displaystyle{ b }[/math], and the function [math]\displaystyle{ \Sigma(b) }[/math] is the total number of polydivisible numbers in base [math]\displaystyle{ b }[/math].

If [math]\displaystyle{ k }[/math] is a polydivisible number in base [math]\displaystyle{ b }[/math] with [math]\displaystyle{ n - 1 }[/math] digits, then it can be extended to create a polydivisible number with [math]\displaystyle{ n }[/math] digits if there is a number between [math]\displaystyle{ bk }[/math] and [math]\displaystyle{ b(k + 1) - 1 }[/math] that is divisible by [math]\displaystyle{ n }[/math]. If [math]\displaystyle{ n }[/math] is less or equal to [math]\displaystyle{ b }[/math], then it is always possible to extend an [math]\displaystyle{ n - 1 }[/math] digit polydivisible number to an [math]\displaystyle{ n }[/math]-digit polydivisible number in this way, and indeed there may be more than one possible extension. If [math]\displaystyle{ n }[/math] is greater than [math]\displaystyle{ b }[/math], it is not always possible to extend a polydivisible number in this way, and as [math]\displaystyle{ n }[/math] becomes larger, the chances of being able to extend a given polydivisible number become smaller. On average, each polydivisible number with [math]\displaystyle{ n - 1 }[/math] digits can be extended to a polydivisible number with [math]\displaystyle{ n }[/math] digits in [math]\displaystyle{ \frac{b}{n} }[/math] different ways. This leads to the following estimate for [math]\displaystyle{ F_{b}(n) }[/math]:

[math]\displaystyle{ F_b(n) \approx (b - 1)\frac{b^{n-1}}{n!}. }[/math]

Summing over all values of n, this estimate suggests that the total number of polydivisible numbers will be approximately

[math]\displaystyle{ \Sigma(b) \approx \frac{b - 1}{b}(e^{b}-1) }[/math]
Base [math]\displaystyle{ b }[/math] [math]\displaystyle{ \Sigma(b) }[/math] Est. of [math]\displaystyle{ \Sigma(b) }[/math] Percent Error
2 2 [math]\displaystyle{ \frac{e^{2} - 1}{2} \approx 3.1945 }[/math] 59.7%
3 15 [math]\displaystyle{ \frac{2}{3}(e^{3} - 1) \approx 12.725 }[/math] -15.1%
4 37 [math]\displaystyle{ \frac{3}{4}(e^{4} - 1) \approx 40.199 }[/math] 8.64%
5 127 [math]\displaystyle{ \frac{4}{5}(e^{5} - 1) \approx 117.93 }[/math] −7.14%
10 20456[2] [math]\displaystyle{ \frac{9}{10}(e^{10} - 1) \approx 19823 }[/math] -3.09%

Specific bases

All numbers are represented in base [math]\displaystyle{ b }[/math], using A−Z to represent digit values 10 to 35.

Base 2

Length n F2(n) Est. of F2(n) Polydivisible numbers
1 1 1 1
2 1 1 10

Base 3

Length n F3(n) Est. of F3(n) Polydivisible numbers
1 2 2 1, 2
2 3 3 11, 20, 22
3 3 3 110, 200, 220
4 3 2 1100, 2002, 2200
5 2 1 11002, 20022
6 2 1 110020, 200220
7 0 0 [math]\displaystyle{ \varnothing }[/math]

Base 4

Length n F4(n) Est. of F4(n) Polydivisible numbers
1 3 3 1, 2, 3
2 6 6 10, 12, 20, 22, 30, 32
3 8 8 102, 120, 123, 201, 222, 300, 303, 321
4 8 8 1020, 1200, 1230, 2010, 2220, 3000, 3030, 3210
5 7 6 10202, 12001, 12303, 20102, 22203, 30002, 32103
6 4 4 120012, 123030, 222030, 321030
7 1 2 2220301
8 0 1 [math]\displaystyle{ \varnothing }[/math]

Base 5

The polydivisible numbers in base 5 are

1, 2, 3, 4, 11, 13, 20, 22, 24, 31, 33, 40, 42, 44, 110, 113, 132, 201, 204, 220, 223, 242, 311, 314, 330, 333, 402, 421, 424, 440, 443, 1102, 1133, 1322, 2011, 2042, 2200, 2204, 2231, 2420, 2424, 3113, 3140, 3144, 3302, 3333, 4022, 4211, 4242, 4400, 4404, 4431, 11020, 11330, 13220, 20110, 20420, 22000, 22040, 22310, 24200, 24240, 31130, 31400, 31440, 33020, 33330, 40220, 42110, 42420, 44000, 44040, 44310, 110204, 113300, 132204, 201102, 204204, 220000, 220402, 223102, 242000, 242402, 311300, 314000, 314402, 330204, 333300, 402204, 421102, 424204, 440000, 440402, 443102, 1133000, 1322043, 2011021, 2042040, 2204020, 2420003, 2424024, 3113002, 3140000, 3144021, 4022042, 4211020, 4431024, 11330000, 13220431, 20110211, 20420404, 24200031, 31400004, 31440211, 40220422, 42110202, 44310242, 132204314, 201102110, 242000311, 314000044, 402204220, 443102421, 1322043140, 2011021100, 3140000440, 4022042200

The smallest base 5 polydivisible numbers with n digits are

1, 11, 110, 1102, 11020, 110204, 1133000, 11330000, 132204314, 1322043140, none...

The largest base 5 polydivisible numbers with n digits are

4, 44, 443, 4431, 44310, 443102, 4431024, 44310242, 443102421, 4022042200, none...

The number of base 5 polydivisible numbers with n digits are

4, 10, 17, 21, 21, 21, 13, 10, 6, 4, 0, 0, 0...
Length n F5(n) Est. of F5(n)
1 4 4
2 10 10
3 17 17
4 21 21
5 21 21
6 21 17
7 13 12
8 10 8
9 6 4
10 4 2

Base 10

The polydivisible numbers in base 10 are

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 102, 105, 108, 120, 123, 126, 129, 141, 144, 147, 162, 165, 168, 180, 183, 186, 189, 201, 204, 207, 222, 225, 228, 243, 246, 249, 261, 264, 267, 282, 285, 288... (sequence A144688 in the OEIS)

The smallest base 10 polydivisible numbers with n digits are

1, 10, 102, 1020, 10200, 102000, 1020005, 10200056, 102000564, 1020005640, 10200056405, 102006162060, 1020061620604, 10200616206046, 102006162060465, 1020061620604656, 10200616206046568, 108054801036000018, 1080548010360000180, 10805480103600001800, ... (sequence A214437 in the OEIS)

The largest base 10 polydivisible numbers with n digits are

9, 98, 987, 9876, 98765, 987654, 9876545, 98765456, 987654564, 9876545640, 98765456405, 987606963096, 9876069630960, 98760696309604, 987606963096045, 9876062430364208, 98485872309636009, 984450645096105672, 9812523240364656789, 96685896604836004260, ... (sequence A225608 in the OEIS)

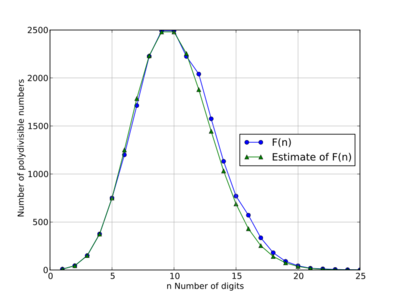
The number of base 10 polydivisible numbers with n digits are

9, 45, 150, 375, 750, 1200, 1713, 2227, 2492, 2492, 2225, 2041, 1575, 1132, 770, 571, 335, 180, 90, 44, 18, 12, 6, 3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ... (sequence A143671 in the OEIS)
Length n F10(n)[5] Est. of F10(n)
1 9 9
2 45 45
3 150 150
4 375 375
5 750 750
6 1200 1250
7 1713 1786
8 2227 2232
9 2492 2480
10 2492 2480
11 2225 2255
12 2041 1879
13 1575 1445
14 1132 1032
15 770 688
16 571 430
17 335 253
18 180 141
19 90 74
20 44 37
21 18 17
22 12 8
23 6 3
24 3 1
25 1 1

Programming example

The example below searches for polydivisible numbers in Python 3.x. 

def find_polydivisible(base: int) -> list[int]:
    """Find polydivisible number."""
    numbers = []
    previous = [i for i in range(1, base)]
    new = []
    digits = 2
    while not previous == []:
        numbers.append(previous)
        for n in previous:
            for j in range(0, base):
                number = n * base + j
                if number % digits == 0:
                    new.append(number)
        previous = new
        new = []
        digits = digits + 1
    return numbers

Older versions of Python do not support annotations using built-in classes. Instead of using list[int], the beginning would become: 

from typing import List
def find_polydivisible(base: int) -> List[int]:

The remaining portion of the program would remain the same.


Related problems

Polydivisible numbers represent a generalization of the following well-known[2] problem in recreational mathematics:

Arrange the digits 1 to 9 in order so that the first two digits form a multiple of 2, the first three digits form a multiple of 3, the first four digits form a multiple of 4 etc. and finally the entire number is a multiple of 9.

The solution to the problem is a nine-digit polydivisible number with the additional condition that it contains the digits 1 to 9 exactly once each. There are 2,492 nine-digit polydivisible numbers, but the only one that satisfies the additional condition is

381 654 729[6]

Other problems involving polydivisible numbers include:

  • Finding polydivisible numbers with additional restrictions on the digits - for example, the longest polydivisible number that only uses even digits is
48 000 688 208 466 084 040
  • Finding palindromic polydivisible numbers - for example, the longest palindromic polydivisible number is
30 000 600 003
  • A common, trivial extension of the aforementioned example is to arrange the digits 0 to 9 to make a 10 digit number in the same way, the result is 3816547290. This is a pandigital polydivisible number.

References

  1. ↑ De, Moloy, MATH'S BELIEVE IT OR NOT, https://www.researchgate.net/publication/317116429 
  2. ↑ 2.0 2.1 2.2 Parker, Matt (2014), "Can you digit?", Things to Make and Do in the Fourth Dimension, Particular Books, pp. 7–8, ISBN 9780374275655, https://books.google.com/books?id=veIxBQAAQBAJ&pg=PA8 
  3. ↑ Wells, David (1986), The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, p. 197, ISBN 9780140261493, https://books.google.com/books?id=kQRPkTkk_VIC&pg=PA197 
  4. ↑ Lines, Malcolm (1986), "How Do These Series End?", A Number for your Thoughts, Taylor and Francis Group, p. 90, ISBN 9780852744956, https://books.google.com/books?id=Am9og6q_ny4C&pg=PA90 
  5. ↑ (sequence A143671 in the OEIS)
  6. ↑ Lanier, Susie, Nine Digit Number, http://jwilson.coe.uga.edu/emt725/Class/Lanier/Nine.Digit/nine.html 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Polydivisible_number&oldid=3380276"