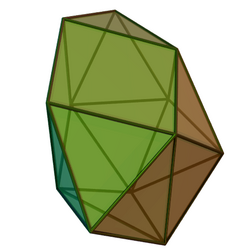
Sphenomegacorona
| Sphenomegacorona | |
|---|---|
 | |
| Type | Johnson J87 – J88 – J89 |
| Faces | 16 triangles 2 squares |
| Edges | 28 |
| Vertices | 12 |
| Vertex configuration | 2(34) 2(32.42) 2x2(35) 4(34.4) |
| Symmetry group | C2v |
| Dual polyhedron | - |
| Properties | convex |
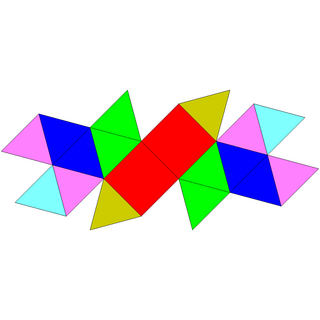
| Net | |
 | |
In geometry, the sphenomegacorona is one of the Johnson solids (J88). It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
Johnson uses the prefix spheno- to refer to a wedge-like complex formed by two adjacent lunes, a lune being a square with equilateral triangles attached on opposite sides. Likewise, the suffix -megacorona refers to a crownlike complex of 12 triangles, contrasted with the smaller triangular complex that makes the sphenocorona. Joining both complexes together results in the sphenomegacorona.[1]
Cartesian coordinates
Let k ≈ 0.59463 be the smallest positive root of the polynomial
- [math]\displaystyle{ \begin{align} &1680 x^{16}- 4800 x^{15} - 3712 x^{14} + 17216 x^{13}+ 1568 x^{12} - 24576 x^{11} + 2464 x^{10} + 17248 x^9 \\ &\quad {}-3384 x^8 - 5584 x^7 + 2000 x^6+ 240 x^5- 776 x^4+ 304 x^3 + 200 x^2 - 56 x -23. \end{align} }[/math]
Then, Cartesian coordinates of a sphenomegacorona with edge length 2 are given by the union of the orbits of the points
- [math]\displaystyle{ \begin{align} &\left(0,1,2\sqrt{1-k^2}\right),\,(2k,1,0),\,\left(0,\frac{\sqrt{3-4k^2}}{\sqrt{1-k^2}}+1,\frac{1-2k^2}{\sqrt{1-k^2}}\right), \\ &\left(1,0,-\sqrt{2+4k-4k^2}\right),\,\left(0,\frac{\sqrt{3-4k^2}\left(2k^2-1\right)}{\left(k^2-1\right)\sqrt{1-k^2}}+1,\frac{2k^4-1}{\left(1-k^2\right)^\frac32}\right) \end{align} }[/math]
under the action of the group generated by reflections about the xz-plane and the yz-plane.[2]
We may then calculate the surface area of a sphenomegacorona of edge length a as
- [math]\displaystyle{ A=\left(2+4\sqrt{3}\right)a^2\approx8.92820a^2, }[/math][3]
and its volume as
- [math]\displaystyle{ V=\xi a^3\approx 1.94811a^3, }[/math]
where the decimal expansion of ξ is given by A334114.[4]
References
- ↑ 1.0 1.1 Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics 18: 169–200, doi:10.4153/cjm-1966-021-8.
- ↑ Timofeenko, A. V. (2009). "The non-Platonic and non-Archimedean noncomposite polyhedra". Journal of Mathematical Science 162 (5): 720. doi:10.1007/s10958-009-9655-0.
- ↑ Wolfram Research, Inc. (2020). Wolfram|Alpha Knowledgebase. Champaign, IL. "
PolyhedronData[{"Johnson", 88}, "SurfaceArea"]". - ↑ OEIS Foundation Inc. (2020), The On-Line Encyclopedia of Integer Sequences, A334114.
External links
 |

