Physics:Transcritical cycle

Short description: Closed thermodynamic cycle involving fluid

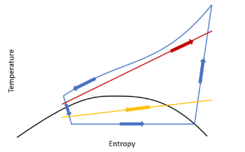
A transcritical cycle is a closed thermodynamic cycle where the working fluid goes through both subcritical and supercritical states. In particular, for power cycles the working fluid is kept in the liquid region during the compression phase and in vapour and/or supercritical conditions during the expansion phase. The ultrasupercritical steam Rankine cycle represents a widespread transcritical cycle in the electricity generation field from fossil fuels, where water is used as working fluid. Other typical applications of transcritical cycles to the purpose of power generation are represented by organic Rankine cycles, which are especially suitable to exploit low temperature heat sources, such as geothermal energy, heat recovery applications or waste to energy plants. With respect to subcritical cycles, the transcritical cycle exploits by definition higher pressure ratios, a feature that ultimately yields higher efficiencies for the majority of the working fluids. Considering then also supercritical cycles as a valid alternative to the transcritical ones, the latter cycles are capable of achieving higher specific works due to the limited relative importance of the work of compression work. This evidences the extreme potential of transcritical cycles to the purpose of producing the most power (measurable in terms of the cycle specific work) with the least expenditure (measurable in terms of spent energy to compress the working fluid).

While in single level supercritical cycles both pressure levels are above the critical pressure of the working fluid, in transcritical cycles one pressure level is above the critical pressure and the other is below. In the refrigeration field carbon dioxide, CO₂, is increasingly considered of interest as refrigerant.

Transcritical conditions of the working fluid

Phase diagram of a generic fluid

TQ diagram of heat introduction to a subcritical and transcritical cold source

In transcritical cycles, the pressure of the working fluid at the outlet of the pump is higher than the critical pressure, while the inlet conditions are close to the saturated liquid pressure at the given minimum temperature.

During the heating phase, which is typically considered an isobaric process, the working fluid overcomes the critical temperature, moving thus from the liquid to the supercritical phase without the occurrence of any evaporation process, a significant difference between subcritical and transcritical cycles. Due to this significant difference in the heating phase, the heat injection into the cycle is significantly more efficient from a second law perspective, since the average temperature difference between the hot source and the working fluid is reduced.

As a consequence, the maximum temperatures reached by the cold source can be higher at fixed hot source characteristics. Therefore, the expansion process can be accomplished exploiting higher pressure ratios, which yields higher power production. Modern ultrasupercritical Rankine cycles can reach maximum temperatures up to 620°C exploiting the optimized heat introduction process.

Characterization of the power cycle

Ts diagrams of subcritical (yellow), transcritical (blue) and supercritical (red) power cycles

Plant layouts of transcritical power cycles (top left), supercritical power cycles (top right), subcritical power cycles (bottom)

As in any power cycle, the most important indicator of its performance is the thermal efficiency. The thermal efficiency of a transcritical cycle is computed as:

[math]\displaystyle{ \eta_{cycle}=\frac{W_{Cycle}}{Q_{in}} }[/math]

where [math]\displaystyle{ Q_{in} }[/math] is the thermal input of the cycle, provided by either combustion or with a heat exchanger, and [math]\displaystyle{ W_{Cycle} }[/math] is the power produced by the cycle.

The power produced is considered comprehensive of the produced power during the expansion process of the working fluid and the one consumed during the compression step.

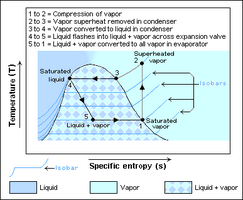
The typical conceptual configuration of a transcritical cycle employs a single heater, thanks to the absence of drastic phase change from one state to another, being the pressure above the critical one. In subcritical cycles, instead, the heating process of the working fluid occurs in three different heat exchangers: in economizers the working fluid is heated (while remaining in the liquid phase) up to a condition approaching the saturated liquid conditions. Evaporators accomplish fluid evaporation process (typically up to the saturated vapour conditions) and in superheaters the working fluid is heated form the saturated vapour conditions to a superheated vapor. Moreover, using Rankine cycles as bottoming cycles in the context of combined gas-steam cycles keeps the configuration of the former ones as always subcritical. Therefore, there will be multiple pressure levels and hence multiple evaporators, economizers and superheaters, which introduces a significant complication to the heat injection process in the cycle.

Characterization of the compression process

Pump diagram

Compressor Stage GE J79

Along adiabatic and isentropic processes, such as those theoretically associated with pumping processes in transcritical cycles, the enthalpy difference across both a compression and an expansion is computed as:

[math]\displaystyle{ \Delta h= \int_{Pmin}^{Pmax} v\cdot dP }[/math]

Consequently, a working fluid with a lower specific volume (hence higher density) can inevitably be compressed spending a lower mechanical work than one with low density (more gas like).

In transcritical cycles, the very high maximum pressures and the liquid conditions along the whole compression phase ensure a higher density and a lower specific volume with respect to supercritical counterparts. Considering the different physical phases though which compression processes occur, transcritical and supercritical cycles employ pumps (for liquids) and compressors (for gases), respectively, during the compression step.

Characterization of the expansion process

Traditional classification of expansions with pure working fluids

TurbineBlades

In the expansion step of the working fluid in transcritical cycles, as in subcritical ones, the working fluid can be discharged either in wet or dry conditions.

Typical dry expansions are those involving organic or other unconventional working fluids, which are characterized by non-negligible molecular complexities and high molecular weights.

The expansion step occurs in turbines: depending on the application and on the nameplate power produced by the power plant, both axial turbines and radial turbines can be exploited during fluid expansion. Axial turbines favour lower rotational speed and higher power production, while radial turbines are suitable for limited powers produced and high rotational speed.

Organic cycles are appropriate choices for low enthalpy applications and are characterized by higher average densities across the expanders than those occurring in transcritical steam cycles: for this reason a low blade height is normally designed and the volumetric flow rate is kept limited to relatively small values. On the other hand in large scale application scenarios the expander blades typically show heights that exceed one meter and that are exploited in the steam cycles. Here, in fact, the fluid density at the outlet of the last expansion stage is significantly low.

In general, the specific work of the cycle is expressed as:

[math]\displaystyle{ w_{Cycle}=\frac{Power_{expansion}-Power_{compression}}{\dot m_{compression}} }[/math]

Even though the specific work of any cycle is strongly dependent on the actual working fluid considered in the cycle, transcritical cycles are expected to exhibit higher specific works than the corresponding subcritical and supercritical counterparts (i.e., that exploit the same working fluid). For this reason, at fixed boundary conditions, power produced and working fluid, a lower mass flow rate is expected in transcritical cycles than in other configurations.

Applications in power cycles

Ultrasupercritical Rankine cycles

Simplified layout of a coal fired power plant

In the last decades, the thermal efficiency of Rankine cycles increased drastically, especially for large scale applications fueled by coal: for these power plants, the application of ultrasupercritical layouts was the main factor to achieve the goal, since the higher pressure ratio ensures higher cycle efficiencies.

The increment in thermal efficiency of power plants fueled by dirty fuels became crucial also in the reduction of the specific emissions of the plants, both in therms of greenhouse gas and for pollutant such as sulfur dioxide or NOx. In large scale applications, ultrasupercritical Rankine cycles employ up to 10 feedwater heaters, five on the high pressure side and five on the low pressure side, including the deaerator, helping in the increment of the temperature at the inlet of the boiler up to 300°C, allowing a significant regenerative air preheating, thus reducing the fuel consumption. Studies on the best performant configurations of supercritical rankine cycles (300 bar of maximum pressure, 600°C of maximum temperature and two reheats) show that such layouts can achieve a cycle efficiency higher than 50%, about 6% higher than subcritical configurations.

Organic Rankine cycles

Internal view of Plug-and-Play Micro-ORC

Ts Diagram of subcritical and transcritical R134a cycles

Organic Rankine cycles are innovative power cycles which allow good performances for low enthalpy thermal sources and ensure condensation above the atmospheric pressure, thus avoiding deaerators and large cross sectional area in the heat rejection units. Moreover, with respect to steam Rankine cycles, ORC have a higher flexibility in handling low power sizes, allowing significant compactness. Typical applications of ORC cover: waste heat recovery plants, geothermal plants, biomass plants and waste to energy power plants.

Organic Rankine cycles use organic fluids (such as hydrocarbons, perfluorocarbons, chlorofluorocarbon, and many others) as working fluids. Most of them have a critical temperature in the range of 100-200°C, for this reason perfectly adaptable to transcritical cycles in low temperature applications. Considering organic fluids, having a maximum pressure above the critical one can more than double the temperature difference across the turbine, with respect to the subcritical counterpart, and significantly increase both the cycle specific work and cycle efficiency.

Applications in refrigeration cycles

A refrigeration cycle, also known as heat pump, is a thermodynamic cycle that allows the removal of heat from a low temperature heat source and the rejection of heat into a high temperature heat source, thanks to mechanical power consumption. Traditional refrigeration cycles are subcritical, with the high pressure side (where heat rejection occurs) below the critical pressure.

Innovative transcritical refrigeration cycles, instead, should use a working fluid whose critical temperature is around the ambient temperature. For this reason, carbon dioxide is chosen due to its favourable critical conditions. In fact, the critical point of carbon dioxide is 31°C, reasonably in between the hot source and cold source of traditional refrigeration applications, thus suitable for a transcritical applications.

In transcritical refrigeration cycles the heat is dissipated through a gas cooler instead of a desuperheater and a condenser like in subcritical cycles. This limits the plant components, plant complexity and costs of the power block.

The advantages of using supercritical carbon dioxide as working fluid, instead of traditional refrigerant fluids (like HFC of HFO), in refrigeration cycles is represented both by economic aspects and environmental ones. The cost of carbon dioxide is two order of magnitude lower than the ones of the average refrigerant working fluid and the environmental impact of carbon dioxide is very limited (with a GWP of 1 and an ODP of 0), the fluid is not reactive nor significantly toxic. No other working fluids for refrigeration is able to reach the same environmental favourable characteristics of carbon dioxide.

• 

  Ts diagram of a transcritical heat pump: cold source (yellow), hot source (red), transcritical cycle (blue)

• 

  A subcritical refrigeration cycle, where heat rejection occurs at a pressure lower than the critical one