List of Johnson solids
In geometry, polyhedra is a three-dimensional object with lines meeting at a point that forms polygons. The points, lines, and polygons of polyhedra are respectively known as the vertices, edges, and faces.[1] A polyhedron is said to be convex if, for every two points inside the polyhedron, there is a line connecting them that lies within the polyhedra as well;[2] its faces are not coplanar (meaning every face are not in the same plane) and its edges are not colinear (meaning the edges are not in the same line).[3] A polyhedron is said to be regular if every polygonal faces are equilateral and equiangular,[4] and those with the polyhedron has vertex-transitive property are called a uniform polyhedron.[5] A Johnson solid (or Johnson–Zalgaller solid) is a convex polyhedron with its faces are regular polygons. Some authors do not require that the Johnson solid not be uniform, meaning that the Johnson solids may not be Platonic solid, Archimedean solid, prism, or antiprism.[6]
The 92 convex polyhedrons were published by Norman Johnson, conjecturing that there are no other solids. His conjecture was proved by Victor Zalgaller proved in 1969 that Johnson's list was complete.[7] Pyramids, cupolae, and rotunda are the first six Johnson solids that have regular faces and convexity. These solids may be applied to construct another polyhedron that has the same properties, a process known as augmentation; attaching prism or antiprism to those is known as elongation or gyroelongation, respectively. Some others may be constructed by diminishment, the removal of those from the component of polyhedra, or by snubification, a construction by cutting loose the edges, lifting the faces and rotate in certain angle, after which adding the equilateral triangles between them.[8]
Every polyhedra has own characteristics, including symmetry and measurement. An object is said to be symmetrical if there is such transformation preserving the immunity to change. All of those transformations may be composed in a concept of group, alongside the number of elements, known as order. In two-dimensional space, these transformations include rotating around the center of a polygon and reflecting an object around the perpendicular bisector of a polygon. A polygon that is rotated symmetrically in [math]\displaystyle{ \frac{360^\circ}{n} }[/math] is denoted by Cn, a cyclic group of order n; combining with the reflection symmetry results in the symmetry of dihedral group Dn of order 2n.[9] In three-dimensional symmetry point groups, the transformation of polyhedra's symmetry includes the rotation around the line passing through the base center, known as axis of symmetry, and reflection relative to perpendicular planes passing through the bisector of a base; this is known as the pyramidal symmetry Cnv of order 2n. Relatedly, polyhedra that preserve their symmetry by rotating it horizontally in [math]\displaystyle{ 180^\circ }[/math] are known as prismatic symmetry Dnv of order 2n. The antiprismatic symmetry Dnd of order 4n preserving the symmetry by rotating its half bottom and reflection across the horizontal plane.[10] The symmetry group Cnh of order 2n preserve the symmetry by rotation around the axis of symmetry and reflection on horizontal plane; one case that preserves the symmetry by one full rotation and one reflection horizontal plane is C1h of order 2, or simply denoted as Cs.[11] The mensuration of polyhedra includes the surface area and volume. An area is a two-dimensional measurement calculated by the product of length and width, and the surface area is the overall area of all faces of polyhedra that is measured by summing all of them.[12] A volume is a measurement of the region in three-dimensional space.[13]
The following table contains the 92 Johnson solids of the edge length a. Each of the columns includes the enumeration of Johnson solid (Jn),[14] the number of vertices, edges, and faces, symmetry, surface area A and volume V.
| Jn | Solid name | Image | Vertices | Edges | Faces | Symmetry group and its order[15] | Surface area and volume[16] |
|---|---|---|---|---|---|---|---|
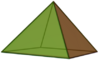
| 1 | Equilateral square pyramid |
|
5 | 8 | 5 | C4v of order 8 | [math]\displaystyle{ \begin{align} A &= \left(1 + \sqrt{3}\right)a^2 \\ &\approx 2.7321a^2 \\ V &= \frac{\sqrt{2}}{6}a^3 \\ &\approx 0.2357a^3 \end{align} }[/math] |
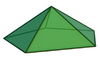
| 2 | Pentagonal pyramid |
|
6 | 10 | 6 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{a^2}{2}\sqrt{\frac{5}{2}\left(10+\sqrt{5}+\sqrt{75+30\sqrt{5}}\right)} \\ &\approx 3.8855a^2 \\ V &= \left(\frac{5 + \sqrt{5}}{24}\right)a^3 \\ &\approx 0.3015a^3 \end{align} }[/math] |
| 3 | Triangular cupola |

|
9 | 15 | 8 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \left(3+\frac{5\sqrt{3}}{2} \right) a^2 \\ &\approx 7.3301a^2 \\ V &= \left(\frac{5}{3\sqrt{2}}\right) a^3 \\ &\approx 1.1785a^3 \end{align} }[/math] |
| 4 | Square cupola |

|
12 | 20 | 10 | C4v of order 8 | [math]\displaystyle{ \begin{align} A &= \left(7+2\sqrt{2}+\sqrt{3}\right)a^2 \\ &\approx 11.5605a^2 \\ V &= \left(1+\frac{2\sqrt{2}}{3}\right)a^3 \\ &\approx 1.9428a^3 \end{align} }[/math] |
| 5 | Pentagonal cupola |

|
15 | 25 | 12 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \left(\frac{1}{4}\left(20+5\sqrt{3}+\sqrt{5\left(145+62\sqrt{5}\right)}\right)\right)a^2 \\ &\approx 16.5798a^2 \\ V &= \left(\frac{1}{6}\left(5+4\sqrt{5}\right)\right)a^3 \\ &\approx 2.3241a^3 \end{align} }[/math] |
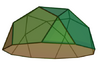
| 6 | Pentagonal rotunda |
|
20 | 35 | 17 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \left(\frac{1}{2}\left(5\sqrt{3}+\sqrt{10\left(65+29\sqrt{5}\right)}\right)\right)a^2 \\ &\approx 22.3472a^2 \\ V &= \left(\frac{1}{12}\left(45+17\sqrt{5}\right)\right)a^3 \\ &\approx 6.9178a^3 \end{align} }[/math] |
| 7 | Elongated triangular pyramid |

|
7 | 12 | 7 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \left(3+\sqrt{3}\right)a^2 \\ &\approx 4.7321a^2 \\ V &= \left(\frac{1}{12}\left(\sqrt{2}+3\sqrt{3}\right)\right)a^3 \\ &\approx 0.5509a^3 \end{align} }[/math] |
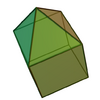
| 8 | Elongated square pyramid |
|
9 | 16 | 9 | C4v of order 8 | [math]\displaystyle{ \begin{align} A &= \left( 5 + \sqrt{3} \right)a^2 \\ &\approx 6.7321a^2 \\ V &= \left( 1 + \frac{\sqrt{2}}{6}\right)a^3 \\ &\approx 1.2357a^3 \end{align} }[/math] |
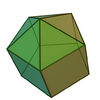
| 9 | Elongated pentagonal pyramid |
|
11 | 20 | 11 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{20 + 5\sqrt{3} + \sqrt{25 + 10\sqrt{5}}}{4}a^2 \\ &\approx 8.8855a^2 \\ V &= \left(\frac{5 + \sqrt{5} + 6\sqrt{25 + 10\sqrt{5}}}{24} \right)a^3 \\ &\approx 2.022a^3 \end{align} }[/math] |
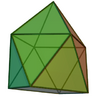
| 10 | Gyroelongated square pyramid |
|
9 | 20 | 13 | C4v of order 8 | [math]\displaystyle{ \begin{align} A &= (1 + 3\sqrt{3})a^2 \\ &\approx 6.1962a^2 \\ V &= \frac{1}{6} \left(\sqrt{2}+2 \sqrt{4+3 \sqrt{2}}\right)a^3 \\ &\approx 1.1927a^3 \end{align} }[/math] |
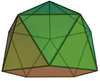
| 11 | Gyroelongated pentagonal pyramid |
|
11 | 25 | 16 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(15 \sqrt{3}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 8.2157a^2 \\ V &= \frac{1}{24} \left(25+9 \sqrt{5}\right)a^3 \\ &\approx 1.8802a^3 \end{align} }[/math] |
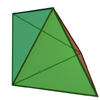
| 12 | Triangular bipyramid |
|
5 | 9 | 6 | D3h of order 12 | [math]\displaystyle{ \begin{align} A &= \frac{3\sqrt{3}}{2}a^2 \\ &\approx 2.5981a^2 \\ V &= \frac{\sqrt{2}}{6}a^3 \\ &\approx 0.2358a^3 \end{align} }[/math] |
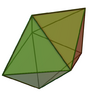
| 13 | Pentagonal bipyramid |
|
7 | 15 | 10 | D5h of order 20 | [math]\displaystyle{ \begin{align} A &= \frac{5 \sqrt{3}}{2}a^2 \\ &\approx 4.3301a^2 \\ V &= \frac{1}{12} \left(5+\sqrt{5}\right)a^3 \\ &\approx 0.603a^3 \end{align} }[/math] |
| 14 | Elongated triangular bipyramid |

|
8 | 15 | 9 | D3h of order 12 | [math]\displaystyle{ \begin{align} A &= \frac{3}{2} \left(2+\sqrt{3}\right)a^2 \\ &\approx 5.5981a^2 \\ V &= \frac{1}{12} \left(2 \sqrt{2}+3 \sqrt{3}\right)a^3 \\ &\approx 0.6687a^3 \end{align} }[/math] |
| 15 | Elongated square bipyramid |

|
10 | 20 | 12 | D4h of order 16 | [math]\displaystyle{ \begin{align} A &= 2 \left(2+\sqrt{3}\right)a^2 \\ &\approx 7.4641a^2 \\ V &= \frac{1}{3} \left(3+\sqrt{2}\right)a^3 \\ &\approx 1.4714a^3 \end{align} }[/math] |
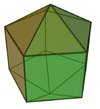
| 16 | Elongated pentagonal bipyramid |
|
12 | 25 | 15 | D5h of order 20 | [math]\displaystyle{ \begin{align} A &= \frac{5}{2} \left(2+\sqrt{3}\right)a^2 \\ &\approx 9.3301a^2 \\ V &= \frac{1}{12} \left(5+\sqrt{5}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^3 \\ &\approx 2.3235a^3 \end{align} }[/math] |
| 17 | Elongated square bipyramid |

|
10 | 24 | 16 | D4d of order 16 | [math]\displaystyle{ \begin{align} A &= 4 \sqrt{3}a^2 \\ &\approx 6.9282a^2 \\ V &= \frac{1}{12} \left(5+\sqrt{5}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^3 \\ &\approx 2.3235a^3 \end{align} }[/math] |
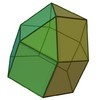
| 18 | Elongated triangular cupola |
|
15 | 27 | 14 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2} \left(18+5 \sqrt{3}\right)a^2 \\ &\approx 13.3301a^2 \\ V &= \frac{1}{3} \left(\sqrt{2}+\sqrt{4+3 \sqrt{2}}\right)a^3 \\ &\approx 1.4284a^3 \end{align} }[/math] |
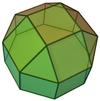
| 19 | Elongated square cupola |
|
20 | 36 | 18 | C4v of order 8 | [math]\displaystyle{ \begin{align} A &= (15+2 \sqrt{2}+\sqrt{3})a^2\\ &\approx 19.5605a^2 \\ V &= \left(3+\frac{8 \sqrt{2}}{3}\right)a^3 \\ &\approx 6.7712a^3 \end{align} }[/math] |
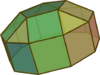
| 20 | Elongated pentagonal cupola |
|
25 | 45 | 22 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(60+5 \sqrt{3}+10 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 26.5798a^2 \\ V &= \frac{1}{6} \left(5+4 \sqrt{5}+15 \sqrt{5+2 \sqrt{5}}\right)a^3 \\ &\approx 10.0183a^3 \end{align} }[/math] |
| 21 | Elongated pentagonal rotunda |

|
30 | 55 | 27 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2}a^2 \left(20+5 \sqrt{3}+5 \sqrt{5+2 \sqrt{5}}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right) \\ &\approx 32.3472a^2 \\ V &= \frac{1}{12}a^3 \left(45+17 \sqrt{5}+30 \sqrt{5+2 \sqrt{5}}\right) \\ &\approx 14.612a^3 \end{align} }[/math] |
| 22 | Gyroelongated triangular cupola |

|
15 | 33 | 20 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2} \left(6+11 \sqrt{3}\right)a^2 \\ &\approx 12.5263a^2 \\ V &= \frac{1}{3} \sqrt{\frac{61}{2}+18 \sqrt{3}+30 \sqrt{1+\sqrt{3}}}a^3 \\ &\approx 3.5161a^3 \end{align} }[/math] |
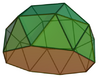
| 23 | Gyroelongated square cupola |
|
20 | 44 | 26 | C4v of order 8 | [math]\displaystyle{ \begin{align} A &= (7+2 \sqrt{2}+5 \sqrt{3})a^2 \\ &\approx 18.4887a^2 \\ V &= \left(1+\frac{2}{3}\sqrt{2} + \frac{2}{3}\sqrt{4+2\sqrt{2}+2\sqrt{146+103\sqrt{2}}}\right)a^3 \\ &\approx 6.2108a^3 \end{align} }[/math] |
| 24 | Gyroelongated pentagonal cupola |

|
25 | 55 | 32 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(20+25 \sqrt{3}+10 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 25.2400a^2 \\ V &= \left(\frac{5}{6}+\frac{2}{3}\sqrt{5} + \frac{5}{6}\sqrt{2\sqrt{650+290\sqrt{5}}-2\sqrt{5}-2}\right) a^3 \\ &\approx 9.0733a^3 \end{align} }[/math] |
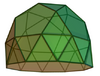
| 25 | Gyroelongated pentagonal rotunda |
|
30 | 65 | 37 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2}\left( 15\sqrt{3}+\left(5+3\sqrt{5}\right)\sqrt{5+2\sqrt{5}}\right)a^2 \\ &\approx 31.0075a^2 \\ V &= \left(\frac{45}{12}+\frac{17}{12}\sqrt{5} + \frac{5}{6}\sqrt{2\sqrt{650+290\sqrt{5}}-2\sqrt{5}-2}\right) a^3 \\ &\approx 13.6671a^3 \end{align} }[/math] |
| 26 | Gyrobifastigium | 
|
8 | 14 | 8 | D2d of order 8 | [math]\displaystyle{ \begin{align} A &= \left(4+\sqrt{3}\right)a^2 \\ &\approx 5.7321a^2 \\ V &= \left(\frac{\sqrt{3}}{2}\right)a^3 \\ &\approx 0.866a^3 \end{align} }[/math] |
| 27 | Triangular orthobicupola |

|
12 | 24 | 14 | D3h of order 12 | [math]\displaystyle{ \begin{align} A &= 2\left(3+\sqrt{3}\right)a^2 \\ &\approx 9.4641a^2 \\ V &= \frac{5\sqrt{2}}{3}a^3 \\ &\approx 2.357a^3 \end{align} }[/math] |
| 28 | Square orthobicupola |

|
16 | 32 | 18 | D4h of order 16 | [math]\displaystyle{ \begin{align} A &= 2(\sqrt{5} + \sqrt{3})a^2 \\ &\approx 13.4641a^2 \\ V &= \left(2 + \frac{4\sqrt{2}}{3}\right)a^3 \\ &\approx 3.8856a^3 \end{align} }[/math] |
| 29 | Square gyrobicupola |

|
16 | 32 | 18 | D4d of order 16 | [math]\displaystyle{ \begin{align} A &= 2(\sqrt{5} + \sqrt{3})a^2 \\ &\approx 13.4641a^2 \\ V &= \left(2 + \frac{4\sqrt{2}}{3}\right)a^3 \\ &\approx 3.8856a^3 \end{align} }[/math] |
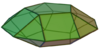
| 30 | Pentagonal orthobicupola |
|
20 | 40 | 22 | D5h of order 20 | [math]\displaystyle{ \begin{align} A &= \left(10+\sqrt{\frac{5}{2}\left(10+\sqrt{5}+\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 17.7711a^2 \\ V &= \frac{1}{3}\left(5+4\sqrt{5}\right)a^3 \\ &\approx 4.6481a^3 \end{align} }[/math] |
| 31 | Pentagonal gyrobicupola |
20 | 40 | 22 | D5d of order 20 | [math]\displaystyle{ \begin{align} A &= \left(10+\sqrt{\frac{5}{2}\left(10+\sqrt{5}+\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 17.7711a^2 \\ V &= \frac{1}{3}\left(5+4\sqrt{5}\right)a^3 \\ &\approx 4.6481a^3 \end{align} }[/math] | |
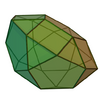
| 32 | Pentagonal orthocupolarotunda |
|
25 | 50 | 27 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \left(5+\frac{1}{4}\sqrt{1900+490\sqrt{5}+210\sqrt{75+30\sqrt{5}}}\right)a^2 \\ &\approx 23.5385a^2 \\ V &= \frac{5}{12}\left(11+5\sqrt{5}\right)a^3 \\ &\approx 9.2418a^3 \end{align} }[/math] |
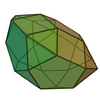
| 33 | Pentagonal gyrocupolarotunda |
|
25 | 50 | 27 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \left(5+\frac{15}{4}\sqrt{3}+\frac{7}{4}\sqrt{25+10\sqrt{5}}\right)a^2 \\ &\approx 23.5385a^2 \\ V &= \frac{5}{12}\left(11+5\sqrt{5}\right)a^3 \\ &\approx 9.2418a^3 \end{align} }[/math] |
| 34 | Pentagonal orthobirotunda |

|
30 | 60 | 32 | D5h of order 20 | [math]\displaystyle{ \begin{align} A &= \left((5 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 29.306a^2 \\ V &= \frac{1}{6}(45 + 17\sqrt{5})a^3 \\ &\approx 13.8355a^3 \end{align} }[/math] |
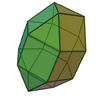
| 35 | Elongated triangular orthobicupola |
|
18 | 36 | 20 | D3h of order 12 | [math]\displaystyle{ \begin{align} A &= 2(6 + \sqrt{3})a^2 \\ &\approx 15.4641a^2 \\ V &= \left(\frac{5 \sqrt{2}}{3} + \frac{3 \sqrt{3}}{2}\right)a^3 \\ &\approx 4.9551a^3 \end{align} }[/math] |
| 36 | Elongated triangular gyrobicupola |

|
18 | 36 | 20 | D3d of order 12 | [math]\displaystyle{ \begin{align} A &= 2(6 + \sqrt{3})a^2 \\ &\approx 15.4641a^2 \\ V &= \left(\frac{5 \sqrt{2}}{3} + \frac{3 \sqrt{3}}{2}\right)a^3 \\ &\approx 4.9551a^3 \end{align} }[/math] |
| 37 | Elongated square gyrobicupola |

|
24 | 48 | 26 | D4d of order 16 | [math]\displaystyle{ \begin{align} A &= 2(9 + \sqrt{3})a^2 \\ &\approx 21.4641a^2 \\ V &= \left(4 + \frac{10\sqrt{2}}{3}\right)a^3 \\ &\approx 8.714a^3 \end{align} }[/math] |
| 38 | Elongated pentagonal orthobicupola |

|
30 | 60 | 32 | D5h of order 20 | [math]\displaystyle{ \begin{align} A &= \left(20+\sqrt{\frac{5}{2}\left(10+\sqrt{5}+\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 27.7711a^2 \\ V &= \frac{1}{6}\left(10+8\sqrt{5}+15\sqrt{5+2\sqrt{5}}\right)a^3 \\ &\approx 12.3423a^3 \end{align} }[/math] |
| 39 | Elongated pentagonal gyrobicupola |

|
30 | 60 | 32 | D5d of order 20 | [math]\displaystyle{ \begin{align} A &= \left(20+\sqrt{\frac{5}{2}\left(10+\sqrt{5}+\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 27.7711a^2 \\ V &= \frac{1}{6}\left(10+8\sqrt{5}+15\sqrt{5+2\sqrt{5}}\right)a^3 \\ &\approx 12.3423a^3 \end{align} }[/math] |
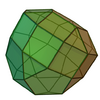
| 40 | Elongated pentagonal orthocupolarotunda |
|
35 | 70 | 37 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4}\left(60+\sqrt{10\left(190+49\sqrt{5}+21\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 33.5385a^2 \\ V &= \frac{5}{12}\left(11+5\sqrt{5}+6\sqrt{5+2\sqrt{5}}\right)a^3 \\ &\approx 16.936a^3 \end{align} }[/math] |
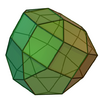
| 41 | Elongated pentagonal gyrocupolarotunda |
|
35 | 70 | 37 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4}\left(60+\sqrt{10\left(190+49\sqrt{5}+21\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 33.5385a^2 \\ V &= \frac{5}{12}\left(11+5\sqrt{5}+6\sqrt{5+2\sqrt{5}}\right)a^3 \\ &\approx 16.936a^3 \end{align} }[/math] |
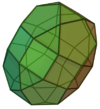
| 42 | Elongated pentagonal orthobirotunda |
|
40 | 80 | 42 | D5h of order 20 | [math]\displaystyle{ \begin{align} A &= \left(10+\sqrt{30\left(10+3\sqrt{5}+\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 39.306a^2 \\ V &= \frac{1}{6}\left(45+17\sqrt{5}+15\sqrt{5+2\sqrt{5}}\right)a^3 \\ &\approx 21.5297a^3 \end{align} }[/math] |
| 43 | Elongated pentaognal gyrobirotunda |

|
40 | 80 | 42 | D5d of order 20 | [math]\displaystyle{ \begin{align} A &= \left(10+\sqrt{30\left(10+3\sqrt{5}+\sqrt{75+30\sqrt{5}}\right)}\right)a^2 \\ &\approx 39.306a^2 \\ V &= \frac{1}{6}\left(45+17\sqrt{5}+15\sqrt{5+2\sqrt{5}}\right)a^3 \\ &\approx 21.5297a^3 \end{align} }[/math] |
| 44 | Gyroelongated triangular bicupola |

|
18 | 42 | 26 | D3 of order 6 | [math]\displaystyle{ \begin{align} A &= \left(6+5\sqrt{3}\right)a^2 \\ &\approx 14.6603a^2 \\ V &= \sqrt{2} \left(\frac{5}{3}+\sqrt{1+\sqrt{3}}\right) a^3 \\ &\approx 4.6946a^3 \end{align} }[/math] |
| 45 | Gyroelongated square bicupola |

|
24 | 56 | 34 | D4 of order 8 | [math]\displaystyle{ \begin{align} A &= \left(10+6\sqrt{3}\right) a^2 \\ &\approx 20.3923a^2 \\ V &= \left(2+\frac{4}{3}\sqrt{2} + \frac{2}{3}\sqrt{4+2\sqrt{2}+2\sqrt{146+103\sqrt{2}}}\right) a^3 \\ &\approx 8.1536a^3 \end{align} }[/math] |
| 46 | Gyroelongated pentagonal bicupola |

|
30 | 70 | 42 | D5 of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2}\left(20+15\sqrt{3}+\sqrt{25+10\sqrt{5}}\right)a^2 \\ &\approx 26.4313a^2 \\ V &= \left(\frac{5}{3}+\frac{4}{3}\sqrt{5} + \frac{5}{6}\sqrt{2\sqrt{650+290\sqrt{5}}-2\sqrt{5}-2}\right) a^3 \\ &\approx 11.3974a^3 \end{align} }[/math] |
| 47 | Gyroelongated pentagonal cupolarotunda |

|
35 | 80 | 47 | C5 of order 5 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4}\left(20+35\sqrt{3}+7\sqrt{25+10\sqrt{5}}\right)a^2 \\ &\approx 32.1988a^2 \\ V &= \left(\frac{55}{12}+\frac{25}{12}\sqrt{5}+ \frac{5}{6}\sqrt{2\sqrt{650+290\sqrt{5}}-2\sqrt{5}-2}\right) a^3 \\ &\approx 15.9911a^3 \end{align} }[/math] |
| 48 | Gyroelongated pentagonal birotunda |

|
40 | 90 | 52 | D5 of order 10 | [math]\displaystyle{ \begin{align} A &= \left(10\sqrt{3} + 3\sqrt{25+10\sqrt{5}}\right) a^2 \\ &\approx 37.9662a^2 \\ V &= \left(\frac{45}{6}+\frac{17}{6}\sqrt{5} + \frac{5}{6}\sqrt{2\sqrt{650+290\sqrt{5}}-2\sqrt{5}-2}\right) a^3 \\ &\approx 20.5848a^3 \end{align} }[/math] |
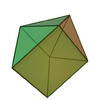
| 49 | Augmented triangular prism |
|
7 | 13 | 8 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2}(4 + 3\sqrt{3})a^2 \\ &\approx 4.5981a^2 \\ V &= \frac{1}{12}(2\sqrt{2} + 3\sqrt{3})a^3 \\ &\approx 0.6687a^3 \end{align} }[/math] |
| 50 | Biaugmented triangular prism |

|
8 | 17 | 11 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2}(2 + 5\sqrt{3})a^2 \\ &\approx 5.3301a^2 \\ V &= \left(\frac{59}{144} + \frac{1}{\sqrt{6}}\right)a^3 \\ &\approx 0.9044a^3 \end{align} }[/math] |
| 51 | Triaugmented triangular prism |

|
9 | 21 | 14 | D3h of order 12 | [math]\displaystyle{ \begin{align} A &= \frac{7\sqrt{3}}{2}a^2 \\ &\approx 6.0622a^2 \\ V &= \frac{2\sqrt{2}+\sqrt{3}}{4}a^3 \\ &\approx 1.1401a^3 \end{align} }[/math] |
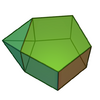
| 52 | Augmented pentagonal prism |
|
11 | 19 | 10 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2} \left(8+2 \sqrt{3}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 9.173a^2 \\ V &= \frac{1}{12} \sqrt{233+90 \sqrt{5}+12 \sqrt{50+20 \sqrt{5}}}a^3 \\ &\approx 1.9562a^3 \end{align} }[/math] |
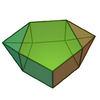
| 53 | Biaugmented pentagonal prism |
|
12 | 23 | 13 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2}a^2 \left(6+4 \sqrt{3}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right) \\ &\approx 9.9051a^2 \\ V &= \frac{1}{12}a^3 \sqrt{257+90 \sqrt{5}+24 \sqrt{50+20 \sqrt{5}}} \\ &\approx 2.1919a^3 \end{align} }[/math] |
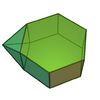
| 54 | Augmented hexagonal prism |
|
13 | 22 | 11 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= (5+4 \sqrt{3})a^2 \\ &\approx 11.9282a^2 \\ V &= \frac{1}{6} \left(\sqrt{2}+9 \sqrt{3}\right)a^3 \\ &\approx 2.8338a^3 \end{align} }[/math] |
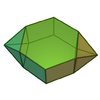
| 55 | Parabiaugmented hexagonal prism |
|
14 | 26 | 14 | D2h of order 8 | [math]\displaystyle{ \begin{align} A &= (4+5 \sqrt{3})a^2 \\ &\approx 12.6603a^2 \\ V &= \frac{1}{6} \left(2 \sqrt{2}+9 \sqrt{3}\right)a^3 \\ &\approx 3.0695a^3 \end{align} }[/math] |
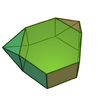
| 56 | Metabiaugmented hexagonal prism |
|
14 | 26 | 14 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= (4+5 \sqrt{3})a^2 \\ &\approx 12.6603a^2 \\ V &= \frac{1}{6} \left(2 \sqrt{2}+9 \sqrt{3}\right)a^3 \\ &\approx 3.0695a^3 \end{align} }[/math] |
| 57 | Triaugmented hexagonal prism |
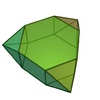
|
15 | 30 | 17 | D3h of order 12 | [math]\displaystyle{ \begin{align} A &= 3 \left(1+2 \sqrt{3}\right)a^2 \\ &\approx 13.3923a^2 \\ V &= \left(\frac{1}{\sqrt{2}}+\frac{3 \sqrt{3}}{2}\right)a^3 \\ &\approx 3.3052a^3 \end{align} }[/math] |
| 58 | Augmented dodecahedron |
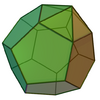
|
21 | 35 | 16 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(5 \sqrt{3}+11 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 21.0903a^2 \\ V &= \frac{1}{24} \left(95+43 \sqrt{5}\right)a^3 \\ &\approx 7.9646a^3 \end{align} }[/math] |
| 59 | Parabiaugmented dodecahedron |

|
22 | 40 | 20 | D5d of order 20 | [math]\displaystyle{ \begin{align} A &= \frac{5}{2} \left(\sqrt{3}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 21.5349a^2 \\ V &= \frac{1}{6} \left(25+11 \sqrt{5}\right)a^3 \\ &\approx 8.2661a^3 \end{align} }[/math] |
| 60 | Metabiaugmented dodecahedron |

|
22 | 40 | 20 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{5}{2} \left(\sqrt{3}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 21.5349a^2 \\ V &= \frac{1}{6} \left(25+11 \sqrt{5}\right)a^3 \\ &\approx 8.2661a^3 \end{align} }[/math] |
| 61 | Triaugmented dodecahedron |

|
23 | 45 | 24 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{3}{4} \left(5 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 21.9795a^2 \\ V &= \frac{5}{8} \left(7+3 \sqrt{5}\right)a^3 \\ &\approx 8.5676a^3 \end{align} }[/math] |
| 62 | Metabidiminished icosahedron |
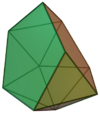
|
10 | 20 | 12 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2} \left(5 \sqrt{3}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 7.7711a^2 \\ V &= \frac{1}{6} \left(5+2 \sqrt{5}\right)a^3 \\ &\approx 1.5787a^3 \end{align} }[/math] |
| 63 | Tridiminished icosahedron |
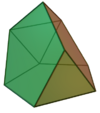
|
9 | 15 | 8 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(5 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^3 \\ &\approx 7.3265a^3 \\ V &= \left(\frac{5}{8}+\frac{7 \sqrt{5}}{24}\right)a^3 \\ &\approx 1.2772a^3 \end{align} }[/math] |
| 64 | Augmented tridiminished icosahedron |
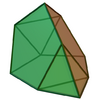
|
10 | 18 | 10 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(7 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 8.1925a^2 \\ V &= \frac{1}{24} \left(15+2 \sqrt{2}+7 \sqrt{5}\right)a^3 \\ &\approx 1.395a^3 \end{align} }[/math] |
| 65 | Augmented truncated tetrahedron |
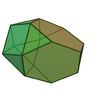
|
15 | 27 | 14 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2} \left(6+13 \sqrt{3}\right)a^2 \\ &\approx 14.2583a^2 \\ V &= \frac{11}{2 \sqrt{2}}a^3 \\ &\approx 3.8891a^3 \end{align} }[/math] |
| 66 | Augmented truncated cube |

|
28 | 48 | 22 | C4v of order 8 | [math]\displaystyle{ \begin{align} A &= (15+10 \sqrt{2}+3 \sqrt{3})a^2 \\ &\approx 34.3383a^2 \\ V &= \left(8+\frac{16 \sqrt{2}}{3}\right)a^3 \\ &\approx 15.5425a^3 \end{align} }[/math] |
| 67 | Biaugmented truncated cube |

|
32 | 60 | 30 | D4h of order 16 | [math]\displaystyle{ \begin{align} A &= 2 \left(9+4 \sqrt{2}+2 \sqrt{3}\right)a^2 \\ &\approx 36.2419a^2 \\ V &= (9+6 \sqrt{2})a^3 \\ &\approx 17.4853a^3 \end{align} }[/math] |
| 68 | Augmented truncated dodecahedron |
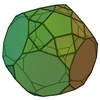
|
65 | 105 | 42 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(20+25 \sqrt{3}+110 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 102.1821a^2 \\ V &= \left(\frac{505}{12}+\frac{81 \sqrt{5}}{4}\right)a^3 \\ &\approx 87.3637a^3 \end{align} }[/math] |
| 69 | Parabiaugmented truncated dodecahedron |
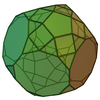
|
70 | 120 | 52 | D5d of order 20 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2} \left(20+15 \sqrt{3}+50 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 103.3734a^2 \\ V &= \frac{1}{12} \left(515+251 \sqrt{5}\right)a^3 \\ &\approx 89.6878a^3 \end{align} }[/math] |
| 70 | Metabiaugmented truncated dodecahedron |
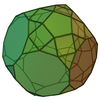
|
70 | 120 | 52 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{1}{2} \left(20+15 \sqrt{3}+50 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 103.3734a^2 \\ V &= \frac{1}{12} \left(515+251 \sqrt{5}\right)a^3 \\ &\approx 89.6878a^3 \end{align} }[/math] |
| 71 | Triaugmented truncated dodecahedron |
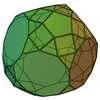
|
75 | 135 | 62 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(60+35 \sqrt{3}+90 \sqrt{5+2 \sqrt{5}}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 104.5648a^2 \\ V &= \frac{7}{12} \left(75+37 \sqrt{5}\right)a^3 \\ &\approx 92.0118a^3 \end{align} }[/math] |
| 72 | Gyrate rhombicosidodecahedron |

|
60 | 120 | 62 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \left(30+5 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 59.306a^2 \\ V &= \left(20+\frac{29 \sqrt{5}}{3}\right)a^3 \\ &\approx 41.6153a^3 \end{align} }[/math] |
| 73 | Parabigyrate rhombicosidodecahedron |

|
60 | 120 | 62 | D5d of order 20 | [math]\displaystyle{ \begin{align} A &= \left(30+5 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 59.306a^2 \\ V &= \left(20+\frac{29 \sqrt{5}}{3}\right)a^3 \\ &\approx 41.6153a^3 \end{align} }[/math] |
| 74 | Metabigyrate rhombicosidodecahedron |

|
60 | 120 | 62 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \left(30+5 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 59.306a^2 \\ V &= \left(20+\frac{29 \sqrt{5}}{3}\right)a^3 \\ &\approx 41.6153a^3 \end{align} }[/math] |
| 75 | Trigyrate rhombicosidodecahedron |

|
60 | 120 | 62 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \left(30+5 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 59.306a^2 \\ V &= \left(20+\frac{29 \sqrt{5}}{3}\right)a^3 \\ &\approx 41.6153a^3 \end{align} }[/math] |
| 76 | Diminished rhombicosidodecahedron |

|
55 | 105 | 52 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(100+15 \sqrt{3}+10 \sqrt{5+2 \sqrt{5}}+11 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 58.1147a^2 \\ V &= \left(\frac{115}{6}+9 \sqrt{5}\right)a^3 \\ &\approx 39.2913a^3 \end{align} }[/math] |
| 77 | Paragyrate diminished rhombicosidodecahedron |

|
55 | 105 | 52 | C5v of order 10 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(100+15 \sqrt{3}+10 \sqrt{5+2 \sqrt{5}}+11 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 58.1147a^2 \\ V &= \left(\frac{115}{6}+9 \sqrt{5}\right)a^3 \\ &\approx 39.2913a^3 \end{align} }[/math] |
| 78 | Metagyrate diminished rhombicosidodecahedron |

|
55 | 105 | 52 | Cs of order 2 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(100+15 \sqrt{3}+10 \sqrt{5+2 \sqrt{5}}+11 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 58.1147a^2 \\ V &= \left(\frac{115}{6}+9 \sqrt{5}\right)a^3 \\ &\approx 39.2913a^3 \end{align} }[/math] |
| 79 | Bigyrate diminished rhombicosidodecahedron |

|
55 | 105 | 52 | Cs of order 2 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(100+15 \sqrt{3}+10 \sqrt{5+2 \sqrt{5}}+11 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 58.1147a^2 \\ V &= \left(\frac{115}{6}+9 \sqrt{5}\right)a^3 \\ &\approx 39.2913a^3 \end{align} }[/math] |
| 80 | Parabidiminished rhombicosidodecahedron |

|
50 | 90 | 42 | D5d of order 20 | [math]\displaystyle{ \begin{align} A &= \frac{5}{2} \left(8+\sqrt{3}+2 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 56.9233a^2 \\ V &= \frac{5}{3} \left(11+5 \sqrt{5}\right)a^3 \\ &\approx 36.9672a^3 \end{align} }[/math] |
| 81 | Metabidiminished rhombicosidodecahedron |

|
50 | 90 | 42 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{5}{2} \left(8+\sqrt{3}+2 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 56.9233a^2 \\ V &= \frac{5}{3} \left(11+5 \sqrt{5}\right)a^3 \\ &\approx 36.9672a^3 \end{align} }[/math] |
| 82 | Gyrate bidiminished rhombicosidodecahedron |

|
50 | 90 | 42 | Cs of order 2 | [math]\displaystyle{ \begin{align} A &= \frac{5}{2} \left(8+\sqrt{3}+2 \sqrt{5+2 \sqrt{5}}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 56.9233a^2 \\ V &= \frac{5}{3} \left(11+5 \sqrt{5}\right)a^3 \\ &\approx 36.9672a^3 \end{align} }[/math] |
| 83 | Tridiminished rhombicosidodecahedron |
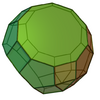
|
45 | 75 | 32 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(60+5 \sqrt{3}+30 \sqrt{5+2 \sqrt{5}}+9 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 55.732a^2 \\ V &= \left(\frac{35}{2}+\frac{23 \sqrt{5}}{3}\right)a^3 \\ &\approx 34.6432a^3 \end{align} }[/math] |
| 84 | Snub disphenoid |
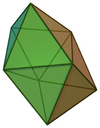
|
8 | 18 | 12 | D2d of order 8 | [math]\displaystyle{ \begin{align} A &= 2 \left(1+3 \sqrt{3}\right)a^2 \\ &\approx 12.3923a^2 \\ V &\approx 0.8595a^3 \end{align} }[/math] |
| 85 | Snub square antiprism |
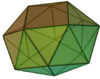
|
16 | 40 | 26 | D4d of order 16 | [math]\displaystyle{ \begin{align} A &= 2 \left(1+3 \sqrt{3}\right)a^2 \\ &\approx 12.3923a^2 \\ V &\approx 3.6012a^3 \end{align} }[/math] |
| 86 | Sphenocorona | 
|
10 | 22 | 14 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= (2+3 \sqrt{3})a^2 \\ &\approx 7.1962a^2 \\ V &= \frac{1}{2}a^3 \sqrt{1+3 \sqrt{\frac{3}{2}}+\sqrt{13+3 \sqrt{6}}} \\ &\approx 1.5154a^3 \end{align} }[/math] |
| 87 | Augmented sphenocorona |

|
11 | 26 | 17 | Cs of order 2 | [math]\displaystyle{ \begin{align} A &= (1+4 \sqrt{3})a^2 \\ &\approx 7.9282a^2 \\ V &= \frac{1}{2}a^3\sqrt{1 + 3 \sqrt{\frac{3}{2}} + \sqrt{13 + 3 \sqrt{6}}}+\frac{1}{3\sqrt{2}} \\ &\approx 1.7511a^3 \end{align} }[/math] |
| 88 | Sphenomegacorona | 
|
12 | 28 | 18 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= 2 \left(1+2 \sqrt{3}\right)a^2 \\ &\approx 8.9282a^2 \\ V &\approx 1.9481a^3 \end{align} }[/math] |
| 89 | Hebesphenomegacorona | 
|
14 | 33 | 21 | C2v of order 4 | [math]\displaystyle{ \begin{align} A &= \frac{3}{2} \left(2+3 \sqrt{3}\right)a^2 \\ &\approx 10.7942a^2 \\ V &\approx 2.9129a^3 \end{align} }[/math] |
| 90 | Disphenocingulum | 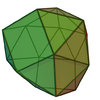
|
16 | 38 | 24 | D2d of order 8 | [math]\displaystyle{ \begin{align} A &= (4+5 \sqrt{3})a^2 \\ &\approx 12.6603a^2 \\ V &\approx 3.7776a^3 \end{align} }[/math] |
| 91 | Bilunabirotunda | 
|
14 | 26 | 14 | D2h of order 8 | [math]\displaystyle{ \begin{align} A &= \left(2+2 \sqrt{3}+\sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 12.346a^2 \\ V &= \frac{1}{12} \left(17+9 \sqrt{5}\right)a^3 \\ &\approx 3.0937a^3 \end{align} }[/math] |
| 92 | Triangular hebespenorotunda |

|
18 | 36 | 20 | C3v of order 6 | [math]\displaystyle{ \begin{align} A &= \frac{1}{4} \left(12+19 \sqrt{3}+3 \sqrt{5 \left(5+2 \sqrt{5}\right)}\right)a^2 \\ &\approx 16.3887a^2 \\ V &= \left(\frac{5}{2}+\frac{7 \sqrt{5}}{6}\right)a^3 \\ &\approx 5.1087a^3 \end{align} }[/math] |
Notes
- ↑ Meyer (2006), p. 418.
- ↑ Litchenberg (1988).
- ↑ Boissonnat & Yvinec (1989).
- ↑ Cromwell (1997), p. 77.
- ↑ Diudea (2018), p. 40.
- ↑ Todesco (2020), p. 282; Williams & Monteleone (2021), p. 23.
- ↑ Johnson (1966); Zalgaller (1969).
- ↑ Rajwade (2001), p. 84–88; Slobodan, Obradović & Ðukanović (2015); Berman (1971), p. 350; Holme (2010), p. 99.
- ↑ Powell (2010), p. 27; Solomon (2003), p. 40.
- ↑ Flusser, Suk & Zitofa (2017), p. 126.
- ↑ Flusser, Suk & Zitofa (2017), p. 126; Hergert & Geilhufe (2018), p. 56.
- ↑ Walsh (2014), p. 284.
- ↑ Parker (1997), p. 264.
- ↑ Uehara (2020), p. 62.
- ↑ Johnson (1966).
- ↑ Berman (1971).
References
- Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8.
- Boissonnat, J. D.; Yvinec, M. (June 1989). "Probing a scene of non convex polyhedra". 237–246. doi:10.1145/73833.73860.
- Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. https://archive.org/details/polyhedra0000crom.
- Diudea, M. V. (2018). Multi-shell Polyhedral Clusters. Springer. doi:10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
- Flusser, Jan; Suk, Tomas; Zitofa, Barbara (2017). 2D and 3D Image Analysis by Moments. John & Sons Wiley.
- Hergert, Wolfram; Geilhufe, Matthias (2018). Group Theory in Solid State Physics and Photonics: Problem Solving with Mathematica. John & Sons Wiley. ISBN 978-3-527-41300-3.
- Holme, Audun (2010). Geometry: Our Cultural Heritage. Springer. doi:10.1007/978-3-642-14441-7. ISBN 978-3-642-14441-7. https://books.google.com/books?id=zXwQGo8jyHUC.
- "Convex Solids with Regular Faces". Canadian Journal of Mathematics 18: 169–200. 1966. doi:10.4153/CJM-1966-021-8.
- Litchenberg, Dorovan R. (1988). "Pyramids, Prisms, Antiprisms, and Deltahedra". The Mathematics Teacher 81 (4): 261-265.
- Meyer, W. (2006). Geometry and Its Applications. Academic Press. ISBN 978-0-12-369427-0. https://books.google.com/books?id=ez6H5Ho6E3cC.
- Parker, Sybil P. (1997). Dictionary of Mathematics. McGraw-Hill.
- Powell, Richard C. (2010). Symmetry, Group Theory, and the Physical Properties of Crystals. Springer. doi:10.1007/978-1-4419-7598-0. ISBN 978-1-4419-7598-0.
- Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
- Solomon, Ronald (2003). Abstract Algebra. American Mathematical Society. ISBN 978-0-8218-4795-4. https://books.google.com/books?id=ouvZKQiykf4C.
- Slobodan, Mišić; Obradović, Marija; Ðukanović, Gordana (2015). "Composite Concave Cupolae as Geometric and Architectural Forms". Journal for Geometry and Graphics 19 (1): 79–91. https://www.heldermann-verlag.de/jgg/jgg19/j19h1misi.pdf.
- Todesco, Gian Marco (2020). "Hyperbolic Honeycomb". Imagine Math 7: Between Culture and Mathematics. Springer. doi:10.1007/978-3-030-42653-8. ISBN 978-3-030-42653-8.
- Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. https://books.google.com/books?id=51juDwAAQBAJ.
- Walsh, Edward T. (2014). A First Course in Geometry. Dover Publications. ISBN 978-0-486-78020-7. https://books.google.com/books?id=ZhDdAwAAQBAJ.
- Williams, Kim; Monteleone, Cosino (2021). Daniele Barbaro’s Perspective of 1568. Springer. doi:10.1007/978-3-030-76687-0. ISBN 978-3-030-76687-0.
- Convex Polyhedra with Regular Faces. Consultants Bureau. 1969.
External links
- Gagnon, Sylvain (1982). "Convex polyhedra with regular faces" (in fr). Topologie Structurale [Structural Topology] (6): 83-95. https://upcommons.upc.edu/bitstream/handle/2099/890/st6-11-a7.pdf.
- Hart, George W.. "Johnson Solid". http://www.georgehart.com/virtual-polyhedra/johnson-info.html.
- "Johnson Polyhedra: Polyhedra with Regular Polygon Faces". https://web.archive.org/web/20130601082835/http://www.uwgb.edu/dutchs/symmetry/johnsonp.htm. See all of the categorized 92 Johnson solids images on one page.
- "Johnson Solids". http://www.orchidpalms.com/polyhedra/johnson/johnson.html.
- Vladimir, Bulatov. "VRML models of Johnson Solids". http://bulatov.org/polyhedra/johnson/.
 |

