Physics:Standard atomic weight

From HandWiki
Short description: Relative atomic mass as defined by IUPAC (CIAAW)
Example: copper in terrestrial sources. Two isotopes are present: copper-63 (62.9) and copper-65 (64.9), in abundances 69% + 31%. The standard atomic weight (Ar°(Cu)) for copper is the average, weighted by their natural abundance, and then divided by the atomic mass constant mu.[1]

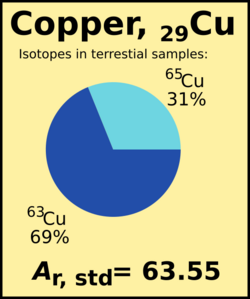
The standard atomic weight of a chemical element (symbol Ar°(E) for element "E") is the weighted arithmetic mean of the relative isotopic masses of all isotopes of that element weighted by each isotope's abundance on Earth. For example, isotope 63Cu (Ar = 62.929) constitutes 69% of the copper on Earth, the rest being 65Cu (Ar = 64.927), so

[math]\displaystyle{ A_\text{r}\text{°}(_\text{29}\text{Cu})=0.69\times62.929+0.31\times64.927=63.55. }[/math]

Because relative isotopic masses are dimensionless quantities, this weighted mean is also dimensionless. It can be converted into a measure of mass (with dimension M) by multiplying it with the dalton, also known as the atomic mass constant.

Among various variants of the notion of atomic weight (Ar, also known as relative atomic mass) used by scientists, the standard atomic weight (Ar°) is the most common and practical. The standard atomic weight of each chemical element is determined and published by the Commission on Isotopic Abundances and Atomic Weights (CIAAW) of the International Union of Pure and Applied Chemistry (IUPAC) based on natural, stable, terrestrial sources of the element. The definition specifies the use of samples from many representative sources from the Earth, so that the value can widely be used as "the" atomic weight for substances as they are encountered in reality—for example, in pharmaceuticals and scientific research. Non-standardized atomic weights of an element are specific to sources and samples, such as the atomic weight of carbon in a particular bone from a particular archeological site. Standard atomic weight averages such values to the range of atomic weights that a chemist might expect to derive from many random samples from Earth. This range is the rationale for the interval notation given for some standard atomic weight values.

Of the 118 known chemical elements, 80 have stable isotopes and 84 have this Earth-environment based value. Typically, such a value is, for example helium: Ar°(He) = 4.002602(2). The "(2)" indicates the uncertainty in the last digit shown, to read 4.002602±0.000002. IUPAC also publishes abridged values, rounded to five significant figures. For helium, Ar, abridged°(He) = 4.0026.

For fourteen elements the samples diverge on this value, because their sample sources have had a different decay history. For example, thallium (Tl) in sedimentary rocks has a different isotopic composition than in igneous rocks and volcanic gases. For these elements, the standard atomic weight is noted as an interval: Ar°(Tl) = [204.38, 204.39]. With such an interval, for less demanding situations, IUPAC also publishes a conventional value. For thallium, Ar, conventional°(Tl) = 204.38.

Definition

Excerpt of an IUPAC Periodic Table showing the interval notation of the standard atomic weights of boron, carbon, and nitrogen (Chemistry International, IUPAC). Example: the pie chart for boron shows it to be composed of about 20% 10B and 80% 11B. This isotope mix causes the atomic weight of ordinary Earthly boron samples to be expected to fall within the interval 10.806 to 10.821. and this interval is the standard atomic weight. Boron samples from unusual sources, particularly non-terrestrial sources, might have measured atomic weights that fall outside this range. Atomic weight and relative atomic mass are synonyms.

The standard atomic weight is a special value of the relative atomic mass. It is defined as the "recommended values" of relative atomic masses of sources in the local environment of the Earth's crust and atmosphere as determined by the IUPAC Commission on Atomic Weights and Isotopic Abundances (CIAAW).[2] In general, values from different sources are subject to natural variation due to a different radioactive history of sources. Thus, standard atomic weights are an expectation range of atomic weights from a range of samples or sources. By limiting the sources to terrestrial origin only, the CIAAW-determined values have less variance, and are a more precise value for relative atomic masses (atomic weights) actually found and used in worldly materials.

The CIAAW-published values are used and sometimes lawfully required in mass calculations. The values have an uncertainty (noted in brackets), or are an expectation interval (see example in illustration immediately above). This uncertainty reflects natural variability in isotopic distribution for an element, rather than uncertainty in measurement (which is much smaller with quality instruments).[3]

Although there is an attempt to cover the range of variability on Earth with standard atomic weight figures, there are known cases of mineral samples which contain elements with atomic weights that are outliers from the standard atomic weight range.[2]

For synthetic elements the isotope formed depends on the means of synthesis, so the concept of natural isotope abundance has no meaning. Therefore, for synthetic elements the total nucleon count of the most stable isotope (i.e., the isotope with the longest half-life) is listed in brackets, in place of the standard atomic weight.

When the term "atomic weight" is used in chemistry, usually it is the more specific standard atomic weight that is implied. It is standard atomic weights that are used in periodic tables and many standard references in ordinary terrestrial chemistry.

Lithium represents a unique case where the natural abundances of the isotopes have in some cases been found to have been perturbed by human isotopic separation activities to the point of affecting the uncertainty in its standard atomic weight, even in samples obtained from natural sources, such as rivers.[citation needed][dubious – discuss]

Terrestrial definition

An example of why "conventional terrestrial sources" must be specified in giving standard atomic weight values is the element argon. Between locations in the Solar System, the atomic weight of argon varies as much as 10%, due to extreme variance in isotopic composition. Where the major source of argon is the decay of 40K in rocks, 40Ar will be the dominant isotope. Such locations include the planets Mercury and Mars, and the moon Titan. On Earth, the ratios of the three isotopes 36Ar : 38Ar : 40Ar are approximately 5 : 1 : 1600, giving terrestrial argon a standard atomic weight of 39.948(1).

However, such is not the case in the rest of the universe. Argon produced directly, by stellar nucleosynthesis, is dominated by the alpha-process nuclide 36Ar. Correspondingly, solar argon contains 84.6% 36Ar (according to solar wind measurements),[4] and the ratio of the three isotopes 36Ar : 38Ar : 40Ar in the atmospheres of the outer planets is 8400 : 1600 : 1.[5] The atomic weight of argon in the Sun and most of the universe, therefore, would be only approximately 36.3.[6]

Causes of uncertainty on Earth

Famously, the published atomic weight value comes with an uncertainty. This uncertainty (and related: precision) follows from its definition, the source being "terrestrial and stable". Systematic causes for uncertainty are:

  1. Measurement limits. As always, the physical measurement is never finite. There is always more detail to be found and read. This applies to every single, pure isotope found. For example, today the mass of the main natural fluorine isotope (fluorine-19) can be measured to the accuracy of eleven decimal places: 18.998403163(6). But a still more precise measurement system could become available, producing more decimals.
  2. Imperfect mixtures of isotopes. In the samples taken and measured the mix (relative abundance) of those isotopes may vary. For example, copper. While in general its two isotopes make out 69.15% and 30.85% each of all copper found, the natural sample being measured can have had an incomplete 'stirring' and so the percentages are different. The precision is improved by measuring more samples of course, but there remains this cause of uncertainty. (Example: lead samples vary so much, it can not be noted more precise than four figures: 207.2)
  3. Earthly sources with a different history. A source is the greater area being researched, for example 'ocean water' or 'volcanic rock' (as opposed to a 'sample': the single heap of material being investigated). It appears that some elements have a different isotopic mix per source. For example, thallium in igneous rock has more lighter isotopes, while in sedimentary rock it has more heavy isotopes. There is no Earthly mean number. These elements show the interval notation: Ar°(Tl) = [204.38, 204.39]. For practical reasons, a simplified 'conventional' number is published too (for Tl: 204.38).

These three uncertainties are accumulative. The published value is a result of all these.

Determination of relative atomic mass

Main page: Chemistry:Isotope geochemistry

Modern relative atomic masses (a term specific to a given element sample) are calculated from measured values of atomic mass (for each nuclide) and isotopic composition of a sample. Highly accurate atomic masses are available[7][8] for virtually all non-radioactive nuclides, but isotopic compositions are both harder to measure to high precision and more subject to variation between samples.[9][10] For this reason, the relative atomic masses of the 22 mononuclidic elements (which are the same as the isotopic masses for each of the single naturally occurring nuclides of these elements) are known to especially high accuracy.

Isotope Atomic mass[8] Abundance[9]
Standard Range
28Si 27.976 926 532 46(194) 92.2297(7)% 92.21–92.25%
29Si 28.976 494 700(22) 4.6832(5)% 4.67–4.69%
30Si 29.973 770 171(32) 3.0872(5)% 3.08–3.10%

The calculation is exemplified for silicon, whose relative atomic mass is especially important in metrology. Silicon exists in nature as a mixture of three isotopes: 28Si, 29Si and 30Si. The atomic masses of these nuclides are known to a precision of one part in 14 billion for 28Si and about one part in one billion for the others. However the range of natural abundance for the isotopes is such that the standard abundance can only be given to about ±0.001% (see table). The calculation is

Ar(Si) = (27.97693 × 0.922297) + (28.97649 × 0.046832) + (29.97377 × 0.030872) = 28.0854

The estimation of the uncertainty is complicated,[11] especially as the sample distribution is not necessarily symmetrical: the IUPAC standard relative atomic masses are quoted with estimated symmetrical uncertainties,[12] and the value for silicon is 28.0855(3). The relative standard uncertainty in this value is 1×10–5 or 10 ppm. To further reflect this natural variability, in 2010, IUPAC made the decision to list the relative atomic masses of 10 elements as an interval rather than a fixed number.[13]

Naming controversy

The use of the name "atomic weight" has attracted a great deal of controversy among scientists.[14] Objectors to the name usually prefer the term "relative atomic mass" (not to be confused with atomic mass). The basic objection is that atomic weight is not a weight, that is the force exerted on an object in a gravitational field, measured in units of force such as the newton or poundal.[citation needed]

In reply, supporters of the term "atomic weight" point out (among other arguments)[14] that:

  • the name has been in continuous use for the same quantity since it was first conceptualized in 1808;[15]
  • for most of that time, atomic weights really were measured by weighing (that is by gravimetric analysis) and the name of a physical quantity should not change simply because the method of its determination has changed;
  • the term "relative atomic mass" should be reserved for the mass of a specific nuclide (or isotope), while "atomic weight" be used for the weighted mean of the atomic masses over all the atoms in the sample;
  • it is not uncommon to have misleading names of physical quantities which are retained for historical reasons, such as

It could be added that atomic weight is often not truly "atomic" either, as it does not correspond to the property of any individual atom. The same argument could be made against "relative atomic mass" used in this sense.

Published values

IUPAC publishes one formal value for each stable chemical element, called the standard atomic weight.[16][1]:{{{1}}} Any updates are published biannually (in uneven years). In 2015, the atomic weight of ytterbium was updated.[16] Per 2017, 14 atomic weights were changed, including argon changing from single number to interval value.[17][18]

The value published can have an uncertainty, like for neon: 20.1797(6), or can be an interval, like for boron: [10.806, 10.821].

Next to these 84 values, IUPAC also publishes abridged values (up to five digits per number only), and for the twelve interval values, conventional values (single number values).

Symbol Ar is a relative atomic mass, for example from a specific sample. To be specific, the standard atomic weight can be noted as Ar°(E), where (E) is the element symbol.

Abridged atomic weight

The abridged atomic weight, also published by CIAAW, is derived from the standard atomic weight reducing the numbers to five digits (five significant figures). The name does not say 'rounded'.

Interval borders are rounded downwards for the first (lowmost) border, and upwards for the upward (upmost) border. This way, the more precise original interval is fully covered.[1]:{{{1}}}

Examples:

  • Calcium: Ar°(Ca) = 40.078(4) → Ar, abridged°(Ca) = 40.078
  • Helium: Ar°(He) = 4.002602(2) → Ar, abridged°(He) = 4.0026
  • Hydrogen: Ar°(H) = [1.00784, 1.00811] → Ar, abridged°(H) = [1.0078, 1.0082]

Conventional atomic weight

Fourteen chemical elements – hydrogen, lithium, boron, carbon, nitrogen, oxygen, magnesium, silicon, sulfur, chlorine, argon, bromine, thallium, and lead – have a standard atomic weight that is defined not as a single number, but as an interval. For example, hydrogen has Ar°(H) = [1.00 784, 1.00811]. This notation states that the various sources on Earth have substantially different isotopic constitutions, and uncertainties are incorporated in the two numbers. For these elements, there is not an 'Earth average' constitution, and the 'right' value is not its middle (that would be 1.007975 for hydrogen, with an uncertainty of (±0.000135) that would make it just cover the interval). However, for situations where a less precise value is acceptable, CIAAW has published a single-number conventional atomic weight that can be used for example in trade. For hydrogen, Ar, conventional°(H) = 1.008.[1]:{{{1}}}

A formal short atomic weight

By using the abridged value, and the conventional value for the fourteen interval values, a short IUPAC-defined value (5 digits plus uncertainty) can be given for all stable elements. In many situations, and in periodic tables, this may be sufficiently detailed.[1]:{{{1}}}

Overview: formal values of the standard atomic weight[1]v · d · e
Element (E)
​ 		Ar, standard(E)
Table 1[19] 		Value type
​ 		Ar, std abridged(E)
Table 2[20] 		Ar, std conventional(E)
Table 3[21] 		Ar, std formal short(E)
Tables 2 ∪ 3[22] 		Mass number
[most stable isotope]
hydrogen 1H [1.00784, 1.00811] Interval [1.0078, 1.0082] 1.008 1.008
nitrogen 7N [14.00643, 14.00728] Interval [14.006, 14.008] 14.007 14.007
fluorine 9F 18.998403163(6) Value (uncertainty) 18.998 18.998
calcium 20Ca 40.078(4) Value (uncertainty) 40.078(4) 40.078(4)
technetium 43Tc (none) Most stable isotope [97]

List of atomic weights

In the periodic table

Group 1 2   3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
Hydrogen &
alkali metals 		Alkaline earth metals Pnicto­gens Chal­co­gens Halo­gens Noble
gases
Period

1

Hydro­gen1H​1.008 He­lium2He​4.0026
2 Lith­ium3Li​6.94 Beryl­lium4Be​9.0122 Boron5B​10.81 Carbon6C​12.011 Nitro­gen7N​14.007 Oxy­gen8O​15.999 Fluor­ine9F​18.998 Neon10Ne​20.180
3 So­dium11Na​22.990 Magne­sium12Mg​24.305 Alumin­ium13Al​26.982 Sili­con14Si​28.085 Phos­phorus15P​30.974 Sulfur16S​32.06 Chlor­ine17Cl​35.45 Argon18Ar​39.95
4 Potas­sium19K​39.098 Cal­cium20Ca​40.078 Scan­dium21Sc​44.956 Tita­nium22Ti​47.867 Vana­dium23V​50.942 Chrom­ium24Cr​51.996 Manga­nese25Mn​54.938 Iron26Fe​55.845 Cobalt27Co​58.933 Nickel28Ni​58.693 Copper29Cu​63.546 Zinc30Zn​65.38 Gallium31Ga​69.723 Germa­nium32Ge​72.630 Arsenic33As​74.922 Sele­nium34Se​78.971 Bromine35Br​79.904 Kryp­ton36Kr​83.798
5 Rubid­ium37Rb​85.468 Stront­ium38Sr​87.62 Yttrium39Y​88.906 Zirco­nium40Zr​91.224 Nio­bium41Nb​92.906 Molyb­denum42Mo​95.95 Tech­netium43Tc​[97] Ruthe­nium44Ru​101.07 Rho­dium45Rh​102.91 Pallad­ium46Pd​106.42 Silver47Ag​107.87 Cad­mium48Cd​112.41 Indium49In​114.82 Tin50Sn​118.71 Anti­mony51Sb​121.76 Tellur­ium52Te​127.60 Iodine53I​126.90 Xenon54Xe​131.29
6 Cae­sium55Cs​132.91 Ba­rium56Ba​137.33 1 asterisk Lute­tium71Lu​174.97 Haf­nium72Hf​178.49 Tanta­lum73Ta​180.95 Tung­sten74W​183.84 Rhe­nium75Re​186.21 Os­mium76Os​190.23 Iridium77Ir​192.22 Plat­inum78Pt​195.08 Gold79Au​196.97 Mer­cury80Hg​200.59 Thallium81Tl​204.38 Lead82Pb​207.2 Bis­muth83Bi​208.98 Polo­nium84Po​[209] Asta­tine85At​[210] Radon86Rn​[222]
7 Fran­cium87Fr​[223] Ra­dium88Ra​[226] 1 asterisk Lawren­cium103Lr​[266] Ruther­fordium104Rf​[267] Dub­nium105Db​[268] Sea­borgium106Sg​[269] Bohr­ium107Bh​[270] Has­sium108Hs​[269] Meit­nerium109Mt​[278] Darm­stadtium110Ds​[281] Roent­genium111Rg​[282] Coper­nicium112Cn​[285] Nihon­ium113Nh​[286] Flerov­ium114Fl​[289] Moscov­ium115Mc​[290] Liver­morium116Lv​[293] Tenness­ine117Ts​[294] Oga­nesson118Og​[294]
1 asterisk Lan­thanum57La​138.91 Cerium58Ce​140.12 Praseo­dymium59Pr​140.91 Neo­dymium60Nd​144.24 Prome­thium61Pm​[145] Sama­rium62Sm​150.36 Europ­ium63Eu​151.96 Gadolin­ium64Gd​157.25 Ter­bium65Tb​158.93 Dyspro­sium66Dy​162.50 Hol­mium67Ho​164.93 Erbium68Er​167.26 Thulium69Tm​168.93 Ytter­bium70Yb​173.05  
1 asterisk Actin­ium89Ac​[227] Thor­ium90Th​232.04 Protac­tinium91Pa​231.04 Ura­nium92U​238.03 Neptu­nium93Np​[237] Pluto­nium94Pu​[244] Ameri­cium95Am​[243] Curium96Cm​[247] Berkel­ium97Bk​[247] Califor­nium98Cf​[251] Einstei­nium99Es​[252] Fer­mium100Fm​[257] Mende­levium101Md​[258] Nobel­ium102No​[259]

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Meija, Juris; Coplen, Tyler B.; Berglund, Michael; Brand, Willi A.; De Bièvre, Paul; Gröning, Manfred; Holden, Norman E.; Irrgeher, Johanna et al. (2016). "Atomic weights of the elements 2013 (IUPAC Technical Report)". Pure and Applied Chemistry 88 (3): 265–91. doi:10.1515/pac-2015-0305. 
  2. ↑ 2.0 2.1 "IUPAC Goldbook". Compendium of Chemical Terminology. doi:10.1351/goldbook.S05907. http://goldbook.iupac.org/terms/view/S05907. Retrieved 12 July 2019. "standard atomic weights: Recommended values of relative atomic masses of the elements revised biennially by the IUPAC Commission on Atomic Weights and Isotopic Abundances and applicable to elements in any normal sample with a high level of confidence. A normal sample is any reasonably possible source of the element or its compounds in commerce for industry and science and has not been subject to significant modification of isotopic composition within a geologically brief period.". 
  3. ↑ Wieser, M. E (2006). "Atomic weights of the elements 2005 (IUPAC Technical Report)". Pure and Applied Chemistry 78 (11): 2051–2066. doi:10.1351/pac200678112051. https://www.iupac.org/publications/pac/2006/pdf/7811x2051.pdf. 
  4. ↑ "The solar argon abundance". Astrophysical Journal 674 (1): 607–611. 2008. doi:10.1086/524725. Bibcode: 2008ApJ...674..607L. 
  5. ↑ Cameron, A. G. W. (1973). "Elemental and isotopic abundances of the volatile elements in the outer planets". Space Science Reviews 14 (3–4): 392–400. doi:10.1007/BF00214750. Bibcode: 1973SSRv...14..392C. 
  6. ↑ This can be determined from the preceding figures per the definition of atomic weight and WP:CALC
  7. ↑ "Atomic Weights and Isotopic Compositions for All Elements". National Institute of Standards and Technology. https://physics.nist.gov/cgi-bin/Compositions/stand_alone.pl?ele=&ascii=html&isotype=some. 
  8. ↑ 8.0 8.1 Wapstra, A.H.; Audi, G.; Thibault, C. (2003), The AME2003 Atomic Mass Evaluation (Online ed.), National Nuclear Data Center, http://www.nndc.bnl.gov/masses/ . Based on:
  9. ↑ 9.0 9.1 Rosman, K. J. R.; Taylor, P. D. P. (1998), "Isotopic Compositions of the Elements 1997", Pure and Applied Chemistry 70 (1): 217–35, doi:10.1351/pac199870010217, http://media.iupac.org/publications/pac/1998/pdf/7001x0217.pdf 
  10. ↑ Coplen, T. B. (2002), "Isotopic Abundance Variations of Selected Elements", Pure and Applied Chemistry 74 (10): 1987–2017, doi:10.1351/pac200274101987, http://www.iupac.org/publications/pac/2002/pdf/7410x1987.pdf 
  11. ↑ Meija, Juris; Mester, Zoltán (2008). "Uncertainty propagation of atomic weight measurement results". Metrologia 45 (1): 53–62. doi:10.1088/0026-1394/45/1/008. Bibcode: 2008Metro..45...53M. 
  12. ↑ Holden, Norman E. (2004). "Atomic Weights and the International Committee—A Historical Review". Chemistry International 26 (1): 4–7. https://media.iupac.org/publications/ci/2004/2601/1_holden.html. 
  13. ↑ "IUPAC – International Union of Pure and Applied Chemistry: Atomic Weights of Ten Chemical Elements About to Change". https://archive.usgs.gov/archive/sites/www.usgs.gov/newsroom/article.asp-ID=2661.html. 
  14. ↑ 14.0 14.1 de Bièvre, Paul; Peiser, H. Steffen (1992). "'Atomic Weight' — The Name, Its History, Definition, and Units". Pure and Applied Chemistry 64 (10): 1535–43. doi:10.1351/pac199264101535. http://www.iupac.org/publications/pac/1992/pdf/6410x1535.pdf. 
  15. ↑ Dalton, John (1808). A New System of Chemical Philosophy. Manchester. https://archive.org/details/newsystemofchemi01daltuoft. 
  16. ↑ 16.0 16.1 "Standard Atomic Weights 2015". Commission on Isotopic Abundances and Atomic Weights. 12 October 2015. http://www.ciaaw.org/atomic-weights.htm. 
  17. ↑ "Standard atomic weights of 14 chemical elements revised". CIAAW. 2018-06-05. https://iupac.org/standard-atomic-weights-of-14-chemical-elements-revised/. 
  18. ↑ "Standard Atomic Weights of 14 Chemical Elements Revised". Chemistry International 40 (4): 23–24. 2018. doi:10.1515/ci-2018-0409. ISSN 0193-6484. 
  19. ↑ Meija 2016, Table 1.
  20. ↑ Meija 2016, Table 2.
  21. ↑ Meija 2016, Table 3.
  22. ↑ Meija 2016, Tables 2 and 3.
  23. ↑ IUPAC 2016, Table 2, 3 combined; uncertainty removed.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Standard_atomic_weight&oldid=3417454"