Charge qubit

Short description: Superconducting qubit implementation

Circuit diagram of a charge qubit circuit. The island (dotted line) is formed by the superconducting electrode between the gate capacitor and the junction capacitance.

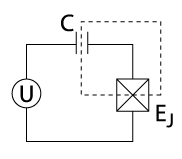
In quantum computing, a charge qubit (also known as Cooper-pair box) is a qubit whose basis states are charge states (i.e. states which represent the presence or absence of excess Cooper pairs in the island). In superconducting quantum computing, a charge qubit is formed by a tiny superconducting island coupled by a Josephson junction (or practically, superconducting tunnel junction) to a superconducting reservoir (see figure). The state of the qubit is determined by the number of Cooper pairs that have tunneled across the junction. In contrast with the charge state of an atomic or molecular ion, the charge states of such an "island" involve a macroscopic number of conduction electrons of the island. The quantum superposition of charge states can be achieved by tuning the gate voltage U that controls the chemical potential of the island. The charge qubit is typically read-out by electrostatically coupling the island to an extremely sensitive electrometer such as the radio-frequency single-electron transistor.

Typical T₂ coherence times for a charge qubit are on the order of 1–2 μs. Recent work has shown T₂ times approaching 100 μs using a type of charge qubit known as a transmon inside a three-dimensional superconducting cavity. Understanding the limits of T₂ is an active area of research in the field of superconducting quantum computing.

Fabrication

Charge qubits are fabricated using techniques similar to those used for microelectronics. The devices are usually made on silicon or sapphire wafers using electron beam lithography (different from phase qubit, which uses photolithography) and metallic thin film evaporation processes. To create Josephson junctions, a technique known as shadow evaporation is normally used; this involves evaporating the source metal alternately at two angles through the lithography defined mask in the electron beam resist. This results in two overlapping layers of the superconducting metal, in between which a thin layer of insulator (normally aluminum oxide) is deposited.

Hamiltonian

If the Josephson junction has a junction capacitance [math]\displaystyle{ C_{\rm J} }[/math], and the gate capacitor [math]\displaystyle{ C_{\rm g} }[/math], then the charging (Coulomb) energy of one Cooper pair is:

[math]\displaystyle{ E_{\rm C}=(2e)^2/2(C_{\rm g}+C_{\rm J}). }[/math]

If [math]\displaystyle{ n }[/math] denotes the number of excess Cooper pairs in the island (i.e. its net charge is [math]\displaystyle{ -2ne }[/math]), then the Hamiltonian is:

[math]\displaystyle{ H=\sum_n \big[E_{\rm C}(n-n_{\rm g})^2 |n \rangle \langle n| - \frac{1}{2} E_{\rm J} (|n \rangle \langle n+1|+|n+1 \rangle \langle n|) \big], }[/math]

where [math]\displaystyle{ n_{\rm g}=C_{\rm g}V_{\rm g}/(2e) }[/math] is a control parameter known as effective offset charge ([math]\displaystyle{ V_{\rm g} }[/math] is the gate voltage), and [math]\displaystyle{ E_{\rm J} }[/math] the Josephson energy of the tunneling junction.

At low temperature and low gate voltage, one can limit the analysis to only the lowest [math]\displaystyle{ n=0 }[/math] and [math]\displaystyle{ n=1 }[/math] states, and therefore obtain a two-level quantum system (a.k.a. qubit).

Note that some recent papers adopt a different notation, and define the charging energy as that of one electron:

[math]\displaystyle{ E_{\rm C}=e^2/2(C_{\rm g}+C_{\rm J}), }[/math]

and then the corresponding Hamiltonian is:

[math]\displaystyle{ H=\sum_n \big[4E_{\rm C}(n-n_{\rm g})^2 |n \rangle \langle n| - \frac{1}{2} E_{\rm J} (|n \rangle \langle n+1|+|n+1 \rangle \langle n|) \big]. }[/math]

Benefits

To-date, the realizations of qubits that have had the most success are ion traps and NMR, with Shor's algorithm even being implemented using NMR. However, it is hard to see these two methods being scaled to the hundreds, thousands, or millions of qubits necessary to create a quantum computer. Solid-state representations of qubits are much more easily scalable, but they themselves have their own problem: decoherence. Superconductors, however, have the advantage of being more easily scaled, and they are more coherent than normal solid-state systems.

Experimental progresses

The implementation of Superconducting charge qubits have been progressing quickly since 1996. Design was theoretically described in 1997 by Shnirman, while the evidence of quantum coherence of the charge in a Cooper pair box was published in February 1997 by Vincent Bouchiat et al. In 1999, coherent oscillations in the charge Qubit were first observed by Nakamura et al. Manipulation of the quantum states and full realization of the charge qubit was observed 2 years later. In 2007, a more advanced device known as Transmon showing enhanced coherence times due to its reduced sensitivity to charge noise was developed at Yale University by Robert J. Schoelkopf, Michel Devoret, Steven M. Girvin and their colleagues .