Grover's algorithm
In quantum computing, Grover's algorithm, also known as the quantum search algorithm, is a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just [math]\displaystyle{ O(\sqrt{N}) }[/math] evaluations of the function, where [math]\displaystyle{ N }[/math] is the size of the function's domain. It was devised by Lov Grover in 1996.[1]
The analogous problem in classical computation cannot be solved in fewer than [math]\displaystyle{ O(N) }[/math] evaluations (because, on average, one has to check half of the domain to get a 50% chance of finding the right input). Charles H. Bennett, Ethan Bernstein, Gilles Brassard, and Umesh Vazirani proved that any quantum solution to the problem needs to evaluate the function [math]\displaystyle{ \Omega(\sqrt{N}) }[/math] times, so Grover's algorithm is asymptotically optimal.[2] Since classical algorithms for NP-complete problems require exponentially many steps, and Grover's algorithm provides at most a quadratic speedup over the classical solution for unstructured search, this suggests that Grover's algorithm by itself will not provide polynomial-time solutions for NP-complete problems (as the square root of an exponential function is an exponential, not polynomial, function).[3]
Unlike other quantum algorithms, which may provide exponential speedup over their classical counterparts, Grover's algorithm provides only a quadratic speedup. However, even quadratic speedup is considerable when [math]\displaystyle{ N }[/math] is large, and Grover's algorithm can be applied to speed up broad classes of algorithms.[3] Grover's algorithm could brute-force a 128-bit symmetric cryptographic key in roughly 264 iterations, or a 256-bit key in roughly 2128 iterations. It may not be the case that Grover's algorithm poses a significantly increased risk to encryption over existing classical algorithms, however.[4]
Applications and limitations
Grover's algorithm, along with variants like amplitude amplification, can be used to speed up a broad range of algorithms.[5][6][7] In particular, algorithms for NP-complete problems generally contain exhaustive search as a subroutine, which can be sped up by Grover's algorithm.[6] The current best algorithm for 3SAT is one such example. Generic constraint satisfaction problems also see quadratic speedups with Grover.[8] These algorithms do not require that the input be given in the form of an oracle, since Grover's algorithm is being applied with an explicit function, e.g. the function checking that a set of bits satisfies a 3SAT instance.
Grover's algorithm can also give provable speedups for black-box problems in quantum query complexity, including element distinctness[9] and the collision problem[10] (solved with the Brassard–Høyer–Tapp algorithm). In these types of problems, one treats the oracle function f as a database, and the goal is to use the quantum query to this function as few times as possible.
Cryptography
Grover's algorithm essentially solves the task of function inversion. Roughly speaking, if we have a function [math]\displaystyle{ y = f(x) }[/math] that can be evaluated on a quantum computer, Grover's algorithm allows us to calculate [math]\displaystyle{ x }[/math] when given [math]\displaystyle{ y }[/math]. Consequently, Grover's algorithm gives broad asymptotic speed-ups to many kinds of brute-force attacks on symmetric-key cryptography, including collision attacks and pre-image attacks.[11] However, this may not necessarily be the most efficient algorithm since, for example, the parallel rho algorithm is able to find a collision in SHA2 more efficiently than Grover's algorithm.[12]
Limitations
Grover's original paper described the algorithm as a database search algorithm, and this description is still common. The database in this analogy is a table of all of the function's outputs, indexed by the corresponding input. However, this database is not represented explicitly. Instead, an oracle is invoked to evaluate an item by its index. Reading a full database item by item and converting it into such a representation may take a lot longer than Grover's search. To account for such effects, Grover's algorithm can be viewed as solving an equation or satisfying a constraint. In such applications, the oracle is a way to check the constraint and is not related to the search algorithm. This separation usually prevents algorithmic optimizations, whereas conventional search algorithms often rely on such optimizations and avoid exhaustive search.[13] Fortunately, fast Grover's oracle implementation is possible for many constraint satisfaction and optimization problems.[14]
The major barrier to instantiating a speedup from Grover's algorithm is that the quadratic speedup achieved is too modest to overcome the large overhead of near-term quantum computers.[15] However, later generations of fault-tolerant quantum computers with better hardware performance may be able to realize these speedups for practical instances of data.
Problem description
As input for Grover's algorithm, suppose we have a function [math]\displaystyle{ f\colon \{0,1,\ldots,N-1\} \to \{0,1\} }[/math]. In the "unstructured database" analogy, the domain represent indices to a database, and f(x) = 1 if and only if the data that x points to satisfies the search criterion. We additionally assume that only one index satisfies f(x) = 1, and we call this index ω. Our goal is to identify ω.
We can access f with a subroutine (sometimes called an oracle) in the form of a unitary operator Uω that acts as follows:
- [math]\displaystyle{ \begin{cases} U_\omega |x\rang = -|x\rang & \text{for } x = \omega \text{, that is, } f(x) = 1, \\ U_\omega |x\rang = |x\rang & \text{for } x \ne \omega \text{, that is, } f(x) = 0. \end{cases} }[/math]
This uses the [math]\displaystyle{ N }[/math]-dimensional state space [math]\displaystyle{ \mathcal{H} }[/math], which is supplied by a register with [math]\displaystyle{ n = \lceil \log_{2} N \rceil }[/math] qubits. This is often written as
- [math]\displaystyle{ U_\omega|x\rang = (-1)^{f(x)}|x\rang. }[/math]
Grover's algorithm outputs ω with probability at least 1/2 using [math]\displaystyle{ O(\sqrt{N}) }[/math] applications of Uω. This probability can be made arbitrarily large by running Grover's algorithm multiple times. If one runs Grover's algorithm until ω is found, the expected number of applications is still [math]\displaystyle{ O(\sqrt{N}) }[/math], since it will only be run twice on average.
Alternative oracle definition
This section compares the above oracle [math]\displaystyle{ U_\omega }[/math] with an oracle [math]\displaystyle{ U_f }[/math].
Uω is different from the standard quantum oracle for a function f. This standard oracle, denoted here as Uf, uses an ancillary qubit system. The operation then represents an inversion (NOT gate) on the main system conditioned by the value of f(x) from the ancillary system:
- [math]\displaystyle{ \begin{cases} U_f |x\rang |y\rang = |x\rang |\neg y\rang & \text{for } x = \omega \text{, that is, } f(x) = 1, \\ U_f |x\rang |y\rang = |x\rang |y\rang & \text{for } x \ne \omega \text{, that is, } f(x) = 0, \end{cases} }[/math]
or briefly,
- [math]\displaystyle{ U_f |x\rang |y\rang = |x\rang |y \oplus f(x)\rang. }[/math]
These oracles are typically realized using uncomputation.
If we are given Uf as our oracle, then we can also implement Uω, since Uω is Uf when the ancillary qubit is in the state [math]\displaystyle{ |-\rang = \frac1{\sqrt2}\big(|0\rang - |1\rang\big) = H|1\rang }[/math]:
- [math]\displaystyle{ \begin{align} U_f \big( |x\rang \otimes |-\rang \big) &= \frac1{\sqrt2} \left( U_f |x\rang |0\rang - U_f |x\rang |1\rang \right)\\ &= \frac1{\sqrt2} \left(|x\rang |f(x)\rang - |x\rang |1 \oplus f(x)\rang \right)\\ &= \begin{cases} \frac1{\sqrt2} \left(-|x\rang |0\rang + |x\rang |1\rang\right) & \text{if } f(x) = 1, \\ \frac1{\sqrt2} \left( |x\rang |0\rang - |x\rang |1\rang \right) & \text{if } f(x) = 0 \end{cases} \\ &= (U_\omega |x\rang) \otimes |-\rang \end{align} }[/math]
So, Grover's algorithm can be run regardless of which oracle is given.[3] If Uf is given, then we must maintain an additional qubit in the state [math]\displaystyle{ |-\rang }[/math] and apply Uf in place of Uω.
Algorithm

The steps of Grover's algorithm are given as follows:
- Initialize the system to the uniform superposition over all states
[math]\displaystyle{ |s\rangle = \frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} |x\rangle. }[/math] - Perform the following "Grover iteration" [math]\displaystyle{ r(N) }[/math] times:
- Apply the operator [math]\displaystyle{ U_\omega }[/math]
- Apply the Grover diffusion operator [math]\displaystyle{ U_s = 2 \left|s\right\rangle \left\langle s\right| - I }[/math]
- Measure the resulting quantum state in the computational basis.
For the correctly chosen value of [math]\displaystyle{ r }[/math], the output will be [math]\displaystyle{ |\omega\rang }[/math] with probability approaching 1 for N ≫ 1. Analysis shows that this eventual value for [math]\displaystyle{ r(N) }[/math] satisfies [math]\displaystyle{ r(N) \leq \Big\lceil\frac{\pi}{4}\sqrt{N}\Big\rceil }[/math].
Implementing the steps for this algorithm can be done using a number of gates linear in the number of qubits.[3] Thus, the gate complexity of this algorithm is [math]\displaystyle{ O(\log(N)r(N)) }[/math], or [math]\displaystyle{ O(\log(N)) }[/math] per iteration.
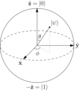
Geometric proof of correctness
There is a geometric interpretation of Grover's algorithm, following from the observation that the quantum state of Grover's algorithm stays in a two-dimensional subspace after each step. Consider the plane spanned by [math]\displaystyle{ |s\rang }[/math] and [math]\displaystyle{ |\omega\rang }[/math]; equivalently, the plane spanned by [math]\displaystyle{ |\omega\rang }[/math] and the perpendicular ket [math]\displaystyle{ \textstyle |s'\rang = \frac{1}{\sqrt{N - 1}}\sum_{x \neq \omega} |x\rang }[/math].
Grover's algorithm begins with the initial ket [math]\displaystyle{ |s\rang }[/math], which lies in the subspace. The operator [math]\displaystyle{ U_{\omega} }[/math] is a reflection at the hyperplane orthogonal to [math]\displaystyle{ |\omega\rang }[/math] for vectors in the plane spanned by [math]\displaystyle{ |s'\rang }[/math] and [math]\displaystyle{ |\omega\rang }[/math], i.e. it acts as a reflection across [math]\displaystyle{ |s'\rang }[/math]. This can be seen by writing [math]\displaystyle{ U_\omega }[/math] in the form of a Householder reflection:
- [math]\displaystyle{ U_\omega = I - 2|\omega\rangle\langle \omega|. }[/math]
The operator [math]\displaystyle{ U_s = 2 |s\rangle \langle s| - I }[/math] is a reflection through [math]\displaystyle{ |s\rang }[/math]. Both operators [math]\displaystyle{ U_s }[/math] and [math]\displaystyle{ U_{\omega} }[/math] take states in the plane spanned by [math]\displaystyle{ |s'\rang }[/math] and [math]\displaystyle{ |\omega\rang }[/math] to states in the plane. Therefore, Grover's algorithm stays in this plane for the entire algorithm.
It is straightforward to check that the operator [math]\displaystyle{ U_s U_{\omega} }[/math] of each Grover iteration step rotates the state vector by an angle of [math]\displaystyle{ \theta = 2\arcsin\tfrac{1}{\sqrt{N}} }[/math]. So, with enough iterations, one can rotate from the initial state [math]\displaystyle{ |s\rang }[/math] to the desired output state [math]\displaystyle{ |\omega\rang }[/math]. The initial ket is close to the state orthogonal to [math]\displaystyle{ |\omega\rang }[/math]:
- [math]\displaystyle{ \lang s'|s\rang = \sqrt{\frac{N-1}{N}}. }[/math]
In geometric terms, the angle [math]\displaystyle{ \theta/2 }[/math] between [math]\displaystyle{ |s\rang }[/math] and [math]\displaystyle{ |s'\rang }[/math] is given by
- [math]\displaystyle{ \sin \frac{\theta}{2} = \frac{1}{\sqrt{N}}. }[/math]
We need to stop when the state vector passes close to [math]\displaystyle{ |\omega\rang }[/math]; after this, subsequent iterations rotate the state vector away from [math]\displaystyle{ |\omega\rang }[/math], reducing the probability of obtaining the correct answer. The exact probability of measuring the correct answer is
- [math]\displaystyle{ \sin^2\left( \Big( r + \frac{1}{2} \Big)\theta\right), }[/math]
where r is the (integer) number of Grover iterations. The earliest time that we get a near-optimal measurement is therefore [math]\displaystyle{ r \approx \pi \sqrt{N} / 4 }[/math].
Algebraic proof of correctness
To complete the algebraic analysis, we need to find out what happens when we repeatedly apply [math]\displaystyle{ U_s U_\omega }[/math]. A natural way to do this is by eigenvalue analysis of a matrix. Notice that during the entire computation, the state of the algorithm is a linear combination of [math]\displaystyle{ s }[/math] and [math]\displaystyle{ \omega }[/math]. We can write the action of [math]\displaystyle{ U_s }[/math] and [math]\displaystyle{ U_\omega }[/math] in the space spanned by [math]\displaystyle{ \{|s\rang, |\omega\rang\} }[/math] as:
- [math]\displaystyle{ U_s : a |\omega \rang + b |s \rang \mapsto [|\omega \rang \, | s \rang] \begin{bmatrix} -1 & 0 \\ 2/\sqrt{N} & 1 \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}. }[/math]
- [math]\displaystyle{ U_\omega : a |\omega \rang + b |s \rang \mapsto [|\omega \rang \, | s \rang] \begin{bmatrix} -1 & -2/\sqrt{N} \\ 0 & 1 \end{bmatrix}\begin{bmatrix}a\\b\end{bmatrix}. }[/math]
So in the basis [math]\displaystyle{ \{ |\omega\rang, |s\rang \} }[/math] (which is neither orthogonal nor a basis of the whole space) the action [math]\displaystyle{ U_sU_\omega }[/math] of applying [math]\displaystyle{ U_\omega }[/math] followed by [math]\displaystyle{ U_s }[/math] is given by the matrix
- [math]\displaystyle{ U_sU_\omega = \begin{bmatrix} -1 & 0 \\ 2/\sqrt{N} & 1 \end{bmatrix} \begin{bmatrix} -1 & -2/\sqrt{N} \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 2/\sqrt{N} \\ -2/\sqrt{N} & 1-4/N \end{bmatrix}. }[/math]
This matrix happens to have a very convenient Jordan form. If we define [math]\displaystyle{ t = \arcsin(1/\sqrt{N}) }[/math], it is
- [math]\displaystyle{ U_sU_\omega = M \begin{bmatrix} e^{2it} & 0 \\ 0 & e^{-2it}\end{bmatrix} M^{-1} }[/math] where [math]\displaystyle{ M = \begin{bmatrix}-i & i \\ e^{it} & e^{-it} \end{bmatrix}. }[/math]
It follows that r-th power of the matrix (corresponding to r iterations) is
- [math]\displaystyle{ (U_sU_\omega)^r = M \begin{bmatrix} e^{2rit} & 0 \\ 0 & e^{-2rit}\end{bmatrix} M^{-1}. }[/math]
Using this form, we can use trigonometric identities to compute the probability of observing ω after r iterations mentioned in the previous section,
- [math]\displaystyle{ \left|\begin{bmatrix}\lang\omega|\omega\rang & \lang\omega|s\rang\end{bmatrix}(U_sU_\omega)^r \begin{bmatrix}0 \\ 1\end{bmatrix} \right|^2 = \sin^2\left( (2r+1)t\right). }[/math]
Alternatively, one might reasonably imagine that a near-optimal time to distinguish would be when the angles 2rt and −2rt are as far apart as possible, which corresponds to [math]\displaystyle{ 2rt \approx \pi/2 }[/math], or [math]\displaystyle{ r = \pi/4t = \pi/4\arcsin(1/\sqrt{N}) \approx \pi\sqrt{N}/4 }[/math]. Then the system is in state
- [math]\displaystyle{ [|\omega \rang \, | s \rang] (U_sU_\omega)^r \begin{bmatrix}0\\1\end{bmatrix} \approx [|\omega \rang \, | s \rang] M \begin{bmatrix} i & 0 \\ 0 & -i\end{bmatrix} M^{-1} \begin{bmatrix}0\\1\end{bmatrix} = | \omega \rang \frac{1}{\cos(t)} - |s \rang \frac{\sin(t)}{\cos(t)}. }[/math]
A short calculation now shows that the observation yields the correct answer ω with error [math]\displaystyle{ O\left (\frac{1}{N} \right) }[/math].
Extensions and variants
Multiple matching entries
If, instead of 1 matching entry, there are k matching entries, the same algorithm works, but the number of iterations must be [math]\displaystyle{ \frac{\pi}{4}{\left( \frac{N}{k} \right)^{1/2}} }[/math]instead of [math]\displaystyle{ \frac{\pi}{4}{N^{1/2}}. }[/math]
There are several ways to handle the case if k is unknown.[16] A simple solution performs optimally up to a constant factor: run Grover's algorithm repeatedly for increasingly small values of k, e.g., taking k = N, N/2, N/4, ..., and so on, taking [math]\displaystyle{ k = N/2^t }[/math] for iteration t until a matching entry is found.
With sufficiently high probability, a marked entry will be found by iteration [math]\displaystyle{ t = \log_2(N/k) + c }[/math] for some constant c. Thus, the total number of iterations taken is at most
- [math]\displaystyle{ \frac{\pi}{4} \Big(1 + \sqrt{2} + \sqrt{4} + \cdots + \sqrt{\frac{N}{k2^c}}\Big) = O\big(\sqrt{N/k}\big). }[/math]
Another approach if k is unknown is to derive it via the quantum counting algorithm prior.
If [math]\displaystyle{ k = N/2 }[/math] (or the traditional one marked state Grover's Algorithm if run with [math]\displaystyle{ N = 2 }[/math]), the algorithm will provide no amplification. If [math]\displaystyle{ k \gt N/2 }[/math], increasing k will begin to increase the number of iterations necessary to obtain a solution.[17] On the other hand, if [math]\displaystyle{ k \geq N/2 }[/math], a classical running of the checking oracle on a single random choice of input will more likely than not give a correct solution.
A version of this algorithm is used in order to solve the collision problem.[18][19]
Quantum partial search
A modification of Grover's algorithm called quantum partial search was described by Grover and Radhakrishnan in 2004.[20] In partial search, one is not interested in finding the exact address of the target item, only the first few digits of the address. Equivalently, we can think of "chunking" the search space into blocks, and then asking "in which block is the target item?". In many applications, such a search yields enough information if the target address contains the information wanted. For instance, to use the example given by L. K. Grover, if one has a list of students organized by class rank, we may only be interested in whether a student is in the lower 25%, 25–50%, 50–75% or 75–100% percentile.
To describe partial search, we consider a database separated into [math]\displaystyle{ K }[/math] blocks, each of size [math]\displaystyle{ b = N/K }[/math]. The partial search problem is easier. Consider the approach we would take classically – we pick one block at random, and then perform a normal search through the rest of the blocks (in set theory language, the complement). If we don't find the target, then we know it's in the block we didn't search. The average number of iterations drops from [math]\displaystyle{ N/2 }[/math] to [math]\displaystyle{ (N-b)/2 }[/math].
Grover's algorithm requires [math]\displaystyle{ \frac{\pi}{4}\sqrt{N} }[/math] iterations. Partial search will be faster by a numerical factor that depends on the number of blocks [math]\displaystyle{ K }[/math]. Partial search uses [math]\displaystyle{ n_1 }[/math] global iterations and [math]\displaystyle{ n_2 }[/math] local iterations. The global Grover operator is designated [math]\displaystyle{ G_1 }[/math] and the local Grover operator is designated [math]\displaystyle{ G_2 }[/math].
The global Grover operator acts on the blocks. Essentially, it is given as follows:
- Perform [math]\displaystyle{ j_1 }[/math] standard Grover iterations on the entire database.
- Perform [math]\displaystyle{ j_2 }[/math] local Grover iterations. A local Grover iteration is a direct sum of Grover iterations over each block.
- Perform one standard Grover iteration.
The optimal values of [math]\displaystyle{ j_1 }[/math] and [math]\displaystyle{ j_2 }[/math] are discussed in the paper by Grover and Radhakrishnan. One might also wonder what happens if one applies successive partial searches at different levels of "resolution". This idea was studied in detail by Vladimir Korepin and Xu, who called it binary quantum search. They proved that it is not in fact any faster than performing a single partial search.
Optimality
Grover's algorithm is optimal up to sub-constant factors. That is, any algorithm that accesses the database only by using the operator Uω must apply Uω at least a [math]\displaystyle{ 1-o(1) }[/math] fraction as many times as Grover's algorithm.[21] The extension of Grover's algorithm to k matching entries, π(N/k)1/2/4, is also optimal.[18] This result is important in understanding the limits of quantum computation.
If the Grover's search problem was solvable with logc N applications of Uω, that would imply that NP is contained in BQP, by transforming problems in NP into Grover-type search problems. The optimality of Grover's algorithm suggests that quantum computers cannot solve NP-Complete problems in polynomial time, and thus NP is not contained in BQP.
It has been shown that a class of non-local hidden variable quantum computers could implement a search of an [math]\displaystyle{ N }[/math]-item database in at most [math]\displaystyle{ O(\sqrt[3]{N}) }[/math] steps. This is faster than the [math]\displaystyle{ O(\sqrt{N}) }[/math] steps taken by Grover's algorithm.[22]
See also
- Amplitude amplification
- Brassard–Høyer–Tapp algorithm (for solving the collision problem)
- Shor's algorithm (for factorization)
- Quantum walk search
Notes
- ↑ Grover, Lov K. (1996-07-01). "A fast quantum mechanical algorithm for database search". Proceedings of the twenty-eighth annual ACM symposium on Theory of computing - STOC '96. Philadelphia, Pennsylvania, USA: Association for Computing Machinery. pp. 212–219. doi:10.1145/237814.237866. ISBN 978-0-89791-785-8. Bibcode: 1996quant.ph..5043G. https://doi.org/10.1145/237814.237866.
- ↑ Bennett C.H.; Bernstein E.; Brassard G.; Vazirani U. (1997). "The strengths and weaknesses of quantum computation". SIAM Journal on Computing 26 (5): 1510–1523. doi:10.1137/s0097539796300933. http://www.cs.berkeley.edu/~vazirani/pubs/bbbv.ps.
- ↑ 3.0 3.1 3.2 3.3 Nielsen, Michael A. (2010). Quantum computation and quantum information. Isaac L. Chuang. Cambridge: Cambridge University Press. pp. 276–305. ISBN 978-1-107-00217-3. OCLC 665137861. https://www.worldcat.org/oclc/665137861.
- ↑ Daniel J. Bernstein (2010-03-03). Grover vs. McEliece. http://cr.yp.to/codes/grovercode-20100303.pdf.
- ↑ Grover, Lov K. (1998). "Proceedings of the Thirtieth Annual ACM Symposium on the Theory of Computing, Dallas, Texas, USA, May 23–26, 1998". in Vitter, Jeffrey Scott. Association for Computing Machinery. pp. 53–62. doi:10.1145/276698.276712.
- ↑ 6.0 6.1 Ambainis, A. (2004-06-01). "Quantum search algorithms". ACM SIGACT News 35 (2): 22–35. doi:10.1145/992287.992296. ISSN 0163-5700. https://doi.org/10.1145/992287.992296.
- ↑ Jordan, Stephen. "Quantum Algorithm Zoo" (in en). https://quantumalgorithmzoo.org.
- ↑ Cerf, Nicolas J.; Grover, Lov K.; Williams, Colin P. (2000-05-01). "Nested Quantum Search and NP-Hard Problems" (in en). Applicable Algebra in Engineering, Communication and Computing 10 (4): 311–338. doi:10.1007/s002000050134. ISSN 1432-0622. https://doi.org/10.1007/s002000050134.
- ↑ Ambainis, Andris (2007-01-01). "Quantum Walk Algorithm for Element Distinctness". SIAM Journal on Computing 37 (1): 210–239. doi:10.1137/S0097539705447311. ISSN 0097-5397. https://epubs.siam.org/doi/10.1137/S0097539705447311.
- ↑ Brassard, Gilles; Høyer, Peter; Tapp, Alain (1998). "LATIN '98: Theoretical Informatics, Third Latin American Symposium, Campinas, Brazil, April, 20-24, 1998, Proceedings". in Lucchesi, Claudio L.; Moura, Arnaldo V.. 1380. Springer. pp. 163–169. doi:10.1007/BFb0054319.
- ↑ Post-quantum cryptography. Daniel J. Bernstein, Johannes Buchmann, Erik, Dipl.-Math Dahmén. Berlin: Springer. 2009. ISBN 978-3-540-88702-7. OCLC 318545517. https://www.worldcat.org/oclc/318545517.
- ↑ Bernstein, Daniel J. (2021-04-21). "Cost analysis of hash collisions: Will quantum computers make SHARCS obsolete?". Conference Proceedings for Special-purpose Hardware for Attacking Cryptographic Systems (SHARCS '09) 09: 105–117. https://www.hyperelliptic.org/tanja/SHARCS/record2.pdf#page=113.
- ↑ Viamontes G.F.; Markov I.L.; Hayes J.P. (2005), "Is Quantum Search Practical?", Computing in Science and Engineering 7 (3): 62–70, doi:10.1109/mcse.2005.53, Bibcode: 2005CSE.....7c..62V, https://web.eecs.umich.edu/~imarkov/pubs/jour/cise05-grov.pdf
- ↑ Sinitsyn N. A.; Yan B. (2023). "Topologically protected Grover's oracle for the partition problem". Physical Review A 108 (2): 022412. doi:10.1103/PhysRevA.108.022412.
- ↑ Babbush, Ryan; McClean, Jarrod R.; Newman, Michael; Gidney, Craig; Boixo, Sergio; Neven, Hartmut (2021-03-29). "Focus beyond Quadratic Speedups for Error-Corrected Quantum Advantage". PRX Quantum 2 (1): 010103. doi:10.1103/PRXQuantum.2.010103.
- ↑ Aaronson, Scott (April 19, 2021). "Introduction to Quantum Information Science Lecture Notes". https://www.scottaaronson.com/qclec.pdf.
- ↑ Nielsen-Chuang
- ↑ 18.0 18.1 Michel Boyer; Gilles Brassard; Peter Høyer; Alain Tapp (1998), "Tight Bounds on Quantum Searching", Fortschr. Phys. 46 (4–5): 493–506, doi:10.1002/3527603093.ch10, ISBN 9783527603091, Bibcode: 1998ForPh..46..493B
- ↑ Andris Ambainis (2004), "Quantum search algorithms", SIGACT News 35 (2): 22–35, doi:10.1145/992287.992296, Bibcode: 2005quant.ph..4012A
- ↑ L.K. Grover; J. Radhakrishnan (2005-02-07). "Is partial quantum search of a database any easier?". arXiv:quant-ph/0407122v4.
- ↑ Zalka, Christof (1999-10-01). "Grover's quantum searching algorithm is optimal". Physical Review A 60 (4): 2746–2751. doi:10.1103/PhysRevA.60.2746. Bibcode: 1999PhRvA..60.2746Z. https://link.aps.org/doi/10.1103/PhysRevA.60.2746.
- ↑ Aaronson, Scott. "Quantum Computing and Hidden Variables". http://www.scottaaronson.com/papers/qchvpra.pdf.
References
- Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212
- Grover L.K.: From Schrödinger's equation to quantum search algorithm, American Journal of Physics, 69(7): 769–777, 2001. Pedagogical review of the algorithm and its history.
- Grover L.K.: QUANTUM COMPUTING: How the weird logic of the subatomic world could make it possible for machines to calculate millions of times faster than they do today The Sciences, July/August 1999, pp. 24–30.
- Nielsen, M.A. and Chuang, I.L. Quantum computation and quantum information. Cambridge University Press, 2000. Chapter 6.
- What's a Quantum Phone Book?, Lov Grover, Lucent Technologies
External links
- Davy Wybiral. "Quantum Circuit Simulator". http://davy.wtf/quantum/?example=Grover%27s%20Algorithm.
- Craig Gidney (2013-03-05). "Grover's Quantum Search Algorithm". http://twistedoakstudios.com/blog/Post2644_grovers-quantum-search-algorithm.
- François Schwarzentruber (2013-05-18). "Grover's algorithm". http://people.irisa.fr/Francois.Schwarzentruber/mit1_algo2_2013/grover_s_algorithm/.
- Alexander Prokopenya. "Quantum Circuit Implementing Grover's Search Algorithm". Wolfram Alpha. http://demonstrations.wolfram.com/QuantumCircuitImplementingGroversSearchAlgorithm/.
- Hazewinkel, Michiel, ed. (2001), "Quantum computation, theory of", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/q130020
- Roberto Maestre (2018-05-11). "Grover's Algorithm implemented in R and C". https://github.com/rmaestre/quantumSystem.
- Bernhard Ömer. "QCL - A Programming Language for Quantum Computers". http://tph.tuwien.ac.at/~oemer/qcl.html. "Implemented in /qcl-0.6.4/lib/grover.qcl"
 |