KLM protocol

From HandWiki

The KLM scheme or KLM protocol is an implementation of linear optical quantum computing (LOQC), developed in 2000 by Emanuel Knill, Raymond Laflamme, and Gerard J. Milburn. This protocol allows for the creation of universal quantum computers using solely linear optical tools.[1] The KLM protocol uses linear optical elements, single-photon sources, and photon detectors as resources to construct a quantum computation scheme involving only ancilla resources, quantum teleportations, and error corrections.

Overview

The KLM scheme induces an effective interaction between photons by making projective measurements with photodetectors, which falls into the category of non-deterministic quantum computation. It is based on a non-linear sign shift between two qubits that uses two ancilla photons and post-selection.[2] It is also based on the demonstrations that the probability of success of the quantum gates can be made close to one by using entangled states prepared non-deterministically and quantum teleportation with single-qubit operations.[3][4] Without a high enough success rate of a single quantum gate unit, it may require an exponential amount of computing resources. The KLM scheme is based on the fact that proper quantum coding can reduce the resources for obtaining accurately encoded qubits efficiently with respect to the accuracy achieved, and can make LOQC fault-tolerant for photon loss, detector inefficiency and phase decoherence. LOQC can be robustly implemented through the KLM scheme with a low enough resource requirement to suggest practical scalability, making it as promising a technology for quantum information processing as other known implementations.

Elements of LOQC in the KLM scheme

Qubits and modes

To avoid losing generality, the discussion below does not limit itself to a particular instance of mode representation. A state written as [math]\displaystyle{ |0,1\rangle _{VH} }[/math] means a state with zero photons in mode [math]\displaystyle{ V }[/math] (could be the "vertical" polarization channel) and one photon in the mode [math]\displaystyle{ H }[/math] (could be the "horizontal" polarization channel).

In the KLM protocol, each of the photons is usually in one of two modes, and the modes are different between the photons (the possibility that a mode is occupied by more than one photon is zero). This is not the case only during implementations of controlled quantum gates such as CNOT. When the state of the system is as described, the photons can be distinguished, since they are in different modes, and therefore a qubit state can be represented using a single photon in two modes, vertical (V) and horizontal (H): for example, [math]\displaystyle{ |0\rangle \equiv |0,1\rangle _{VH} }[/math] and [math]\displaystyle{ |1\rangle \equiv |1,0\rangle _{VH} }[/math]. It is common to refer to the states defined via occupation of modes as Fock states.

Such notations are useful in quantum computing, quantum communication and quantum cryptography. For example, it is very easy to consider a loss of a single photon using these notations, simply by adding the vacuum state [math]\displaystyle{ |0,0\rangle _{VH} }[/math] containing zero photons in those two modes. As another example, when having two photons in two separated modes (e.g. two time bins or two arms of an interferometer), it is easy to describe an entangled state of the two photons. The singlet state (two linked photons with overall spin quantum number [math]\displaystyle{ s=0 }[/math]) can be described as follows: if [math]\displaystyle{ |1,0\rangle _{VH}^a, |0,1\rangle _{VH}^a }[/math] and [math]\displaystyle{ |1,0\rangle _{VH}^b, |0,1\rangle _{VH}^b }[/math] describe the basis states of the two separated modes, then the singlet state is [math]\displaystyle{ (|1,0\rangle _{VH}^a |0,1\rangle _{VH}^b - |0,1\rangle _{VH}^a |1,0\rangle _{VH}^b)/\sqrt2. }[/math]

State measurement/readout

In the KLM protocol, a quantum state can be read out or measured using photon detectors along selected modes. If a photodetector detects a photon signal in a given mode, it means the corresponding mode state is a 1-photon state before measuring. As discussed in KLM's proposal,[1] photon loss and detection efficiency dramatically influence the reliability of the measurement results. The corresponding failure issue and error correction methods will be described later.

A left-pointed triangle will be used in circuit diagrams to represent the state readout operator in this article.[1]

Implementations of elementary quantum gates

Ignoring error correction and other issues, the basic principle in implementations of elementary quantum gates using only mirrors, beam splitters and phase shifters is that by using these linear optical elements, one can construct any arbitrary 1-qubit unitary operation; in other words, those linear optical elements support a complete set of operators on any single qubit.

The unitary matrix associated with a beam splitter [math]\displaystyle{ \mathbf{B}_{\theta,\phi} }[/math] is:

[math]\displaystyle{ U(\mathbf{B}_{\theta,\phi}) =\begin{bmatrix} \cos \theta & -e^{i\phi}\sin \theta \\ e^{-i\phi} \sin \theta & \cos \theta \end{bmatrix} }[/math],

where [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math] are determined by the reflection amplitude [math]\displaystyle{ r }[/math] and the transmission amplitude [math]\displaystyle{ t }[/math] (relationship will be given later for a simpler case). For a symmetric beam splitter, which has a phase shift [math]\displaystyle{ \phi=\frac{\pi}{2} }[/math] under the unitary transformation condition [math]\displaystyle{ |t|^2+|r|^2=1 }[/math] and [math]\displaystyle{ t^*r+tr^*=0 }[/math], one can show that

[math]\displaystyle{ U(\mathbf{B}_{\theta,\phi=\frac{\pi}{2}}) =\begin{bmatrix} t & r\\ r & t\end{bmatrix} =\begin{bmatrix} \cos \theta & -i\sin \theta \\ -i \sin \theta & \cos \theta \end{bmatrix}=\cos \theta \hat{I}-i \sin \theta \hat{\sigma}_x=e^{-i\theta\hat{\sigma}_x} }[/math],

which is a rotation of the single qubit state about the [math]\displaystyle{ x }[/math]-axis by [math]\displaystyle{ 2\theta=2\cos^{-1}(|t|) }[/math] in the Bloch sphere.

A mirror is a special case where the reflecting rate is 1, so that the corresponding unitary operator is a rotation matrix given by

[math]\displaystyle{ R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{bmatrix} }[/math].

For most cases of beam splitters used in QIP, the incident angle [math]\displaystyle{ \theta=45^\circ }[/math].

Similarly, a phase shifter operator [math]\displaystyle{ \mathbf{P}_\phi }[/math] associates with a unitary operator described by [math]\displaystyle{ U(\mathbf{P}_\phi)=e^{i\phi} }[/math], or, if written in a 2-mode format

[math]\displaystyle{ U(\mathbf{P}_{\phi})= \begin{bmatrix} e^{i\phi} & 0 \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} e^{i\phi/2} & 0\\ 0 & e^{-i\phi/2}\end{bmatrix} \text{(global phase ignored)}=e^{i\frac{\phi}{2} \hat{\sigma}_z} }[/math],

which is equivalent to a rotation of [math]\displaystyle{ -\phi }[/math] about the [math]\displaystyle{ z }[/math]-axis.

Since any two [math]\displaystyle{ SU(2) }[/math] rotations along orthogonal rotating axes can generate arbitrary rotations in the Bloch sphere, one can use a set of symmetric beam splitters and mirrors to realize an arbitrary [math]\displaystyle{ SU(2) }[/math] operators for QIP. The figures below are examples of implementing a Hadamard gate and a Pauli-X-gate (NOT gate) by using beam splitters (illustrated as rectangles connecting two sets of crossing lines with parameters [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math]) and mirrors (illustrated as rectangles connecting two sets of crossing lines with parameter [math]\displaystyle{ R(\theta) }[/math]).

Implementation of a Hadamard gate with a beam splitter and a mirror. Quantum circuit is on the top part.
Implementation of a Pauli-X gate (NOT gate) with a beam splitter. Quantum circuit is on the top part.

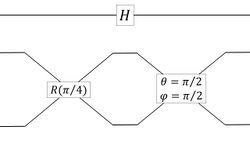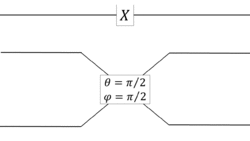In the above figures, a qubit is encoded using two mode channels (horizontal lines): [math]\displaystyle{ \left\vert0\right\rangle }[/math] represents a photon in the top mode, and [math]\displaystyle{ \left\vert1\right\rangle }[/math] represents a photon in the bottom mode.

In the KLM scheme, qubit manipulations are realized via a series of non-deterministic operations with increasing probability of success. The first improvement to this implementation that will be discussed is the nondeterministic conditional sign flip gate.

Implementation of nondeterministic conditional sign flip gate

An important element of the KLM scheme is the conditional sign flip or nonlinear sign flip gate (NS-gate) as shown in the figure below on the right. It gives a nonlinear phase shift on one mode conditioned on two ancilla modes.

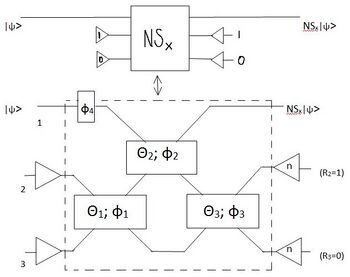
Linear optics implementation of NS-gate. The elements framed in the box with dashed border is the linear optics implementation with three beam splitters and one phase shifter (see text for parameters). Modes 2 and 3 are ancilla modes.

In the picture on the right, the labels on the left of the bottom box indicate the modes. The output is accepted only if there is one photon in mode 2 and zero photons in mode 3 detected, where the ancilla modes 2 and 3 are prepared as the [math]\displaystyle{ |1,0\rangle_{2,3} }[/math] state. The subscript [math]\displaystyle{ x }[/math] is the phase shift of the output, and is determined by the parameters of inner optical elements chosen.[1] For [math]\displaystyle{ x=-1 }[/math] case, the following parameters are used: [math]\displaystyle{ \theta_1=22.5^\circ }[/math], [math]\displaystyle{ \phi_1=0^\circ }[/math], [math]\displaystyle{ \theta_2=65.5302^\circ }[/math], [math]\displaystyle{ \phi_2=0^\circ }[/math], [math]\displaystyle{ \theta_3=-22.5^\circ }[/math], [math]\displaystyle{ \phi_3=0^\circ }[/math], and [math]\displaystyle{ \phi_4=180^\circ }[/math]. For the [math]\displaystyle{ x=e^{i\pi/2} }[/math] case, the parameters can be chosen as [math]\displaystyle{ \theta_1=36.53^\circ }[/math], [math]\displaystyle{ \phi_1=88.24^\circ }[/math], [math]\displaystyle{ \theta_2=62.25^\circ }[/math], [math]\displaystyle{ \phi_2=-66.53^\circ }[/math], [math]\displaystyle{ \theta_3=-36.53^\circ }[/math], [math]\displaystyle{ \phi_3=-11.25^\circ }[/math], and [math]\displaystyle{ \phi_4=102.24^\circ }[/math]. Similarly, by changing the parameters of beam splitters and phase shifters, or by combining multiple NS gates, one can create various quantum gates. By sharing two ancilla modes, Knill invented the following controlled-Z gate (see the figure on the right) with success rate of 2/27.[5]

Linear optics implementation of Controlled-Z Gate with ancilla modes labelled as 2 and 3. [math]\displaystyle{ \theta=54.74^\circ }[/math] and [math]\displaystyle{ \theta'=17.63^\circ }[/math].

The advantage of using NS gates is that the output can be guaranteed conditionally processed with some success rate which can be improved to nearly 1. Using the configuration as shown in the figure above on the right, the success rate of an [math]\displaystyle{ x=-1 }[/math] NS gate is [math]\displaystyle{ 1/4 }[/math]. To further improve successful rate and solve the scalability problem, one needs to use gate teleportation, described next.

Gates teleportation and near-deterministic gates

Given the use of non-deterministic quantum gates for KLM, there may be only a very small probability [math]\displaystyle{ p^N }[/math] that a circuit with [math]\displaystyle{ N }[/math] gates with a single-gate success possibility of [math]\displaystyle{ p }[/math] will work perfectly by running the circuit once. Therefore, the operations must on average be repeated on the order of [math]\displaystyle{ p^{-N} }[/math] times or [math]\displaystyle{ p^{-N} }[/math] such systems must be run in parallel. Either way, the required time or circuit resources scale exponentially.[citation needed] In 1999, Gottesman and Chuang pointed out that one can prepare the probabilistic gates offline from the quantum circuit by using quantum teleportation.[4] The basic idea is that each probabilistic gate is prepared offline, and the successful event signal is teleported back to the quantum circuit. An illustration of quantum teleportation is given in the figure on the right. As can be seen, the quantum state in mode 1 is teleported to mode 3 through a Bell measurement and an entangled resource Bell state [math]\displaystyle{ |\Phi^+\rangle = \frac{1}{\sqrt{2}} (|01\rangle + |10\rangle) }[/math], where the state 1 may be regarded as prepared offline.

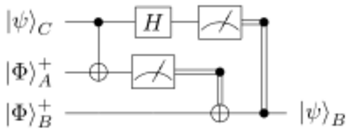
The resource Bell state [math]\displaystyle{ |\Phi^+\rangle }[/math] can be generated from the state [math]\displaystyle{ |10\rangle }[/math] by use of a mirror with parameter [math]\displaystyle{ \theta = \frac{\pi}{4}. }[/math]

Quantum circuit representation of quantum teleportation.

By using teleportation, many probabilistic gates may be prepared in parallel with [math]\displaystyle{ n }[/math]-photon entangled states, sending a control signal to the output mode. Through using [math]\displaystyle{ n }[/math] probabilistic gates in parallel offline, a success rate of [math]\displaystyle{ \frac{n^2}{(n+1)^2} }[/math] can be obtained, which is close to 1 as [math]\displaystyle{ n }[/math] becomes large. The number of gates needed to realize a certain accuracy scales polynomially rather than exponentially. In this sense, the KLM protocol is resource-efficient. One experiment using the KLM originally proposed controlled-NOT gate with four-photon input was demonstrated in 2011,[6] and gave an average fidelity of [math]\displaystyle{ F=0.82\pm 0.01 }[/math].

Error detection and correction

As discussed above, the success probability of teleportation gates can be made arbitrarily close to 1 by preparing larger entangled states. However, the asymptotic approach to the probability of 1 is quite slow with respect to the photon number [math]\displaystyle{ n }[/math]. A more efficient approach is to encode against gate failure (error) based on the well-defined failure mode of the teleporters. In the KLM protocol, the teleporter's failure can be diagnosed if zero or [math]\displaystyle{ n+1 }[/math] photons are detected. If the computing device can be encoded against accidental measurements of some certain number of photons, then it will be possible to correct gate failures and the probability of eventually successfully applying the gate will increase.

Many experimental trials using this idea have been carried out (see, for example, Refs[7][8][9]). However, a large number of operations are still needed to achieve a success probability very close to 1. In order to promote the KLM protocol as a viable technology, more efficient quantum gates are needed. This is the subject of the next part.

Improvements

This section discusses the improvements of the KLM protocol that have been studied after the initial proposal.

There are many ways to improve the KLM protocol for LOQC and to make LOQC more promising. Below are some proposals from the review article Ref.[10] and other subsequent articles:

There are several protocols for using cluster states to improve the KLM protocol, the computation model with those protocols is an LOQC implementation of the one-way quantum computer:

  • The Yoran-Reznik protocol - this protocol makes use of cluster-chains in order to increase the success probability of teleportation.
  • The Nielsen protocol - this protocol improves the Yoran-Reznik protocol by first using teleportation to add qubits to cluster-chains and then uses the enlarged cluster chains to further increase the success probability of teleportation.
  • The Browne-Rudolph protocol - this protocol improves the Nielsen protocol by using teleportation not only to add qubits to cluster-chains but also to fuse them .

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 Knill, E.; Laflamme, R.; Milburn, G. J. (2001). "A scheme for efficient quantum computation with linear optics". Nature (Nature Publishing Group) 409 (6816): 46–52. doi:10.1038/35051009. PMID 11343107. Bibcode: 2001Natur.409...46K. 
  2. ↑ Adleman, Leonard M.; DeMarrais, Jonathan; Huang, Ming-Deh A. (1997). "Quantum Computability". SIAM Journal on Computing 26 (5): 1524–1540. doi:10.1137/S0097539795293639. ISSN 0097-5397. 
  3. ↑ Bennett, Charles H.; Brassard, Gilles; Crépeau, Claude; Jozsa, Richard; Peres, Asher; Wootters, William K. (1993-03-29). "Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels". Physical Review Letters 70 (13): 1895–1899. doi:10.1103/PhysRevLett.70.1895. PMID 10053414. Bibcode: 1993PhRvL..70.1895B. 
  4. ↑ 4.0 4.1 Gottesman, Daniel; Chuang, Isaac L. (1999-11-25). "Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations". Nature 402 (6760): 390–393. doi:10.1038/46503. ISSN 0028-0836. Bibcode: 1999Natur.402..390G. 
  5. ↑ Knill, E. (2002-11-14). "Quantum gates using linear optics and postselection". Physical Review A 66 (5): 052306. doi:10.1103/PhysRevA.66.052306. Bibcode: 2002PhRvA..66e2306K. 
  6. ↑ Okamoto, Ryo; O’Brien, Jeremy L.; Hofmann, Holger F.; Takeuchi, Shigeki (2011-06-21). "Realization of a Knill-Laflamme-Milburn controlled-NOT photonic quantum circuit combining effective optical nonlinearities". Proceedings of the National Academy of Sciences 108 (25): 10067–10071. doi:10.1073/pnas.1018839108. ISSN 0027-8424. PMID 21646543. Bibcode: 2011PNAS..10810067O. 
  7. ↑ O’Brien, J. L.; Pryde, G. J.; White, A. G.; Ralph, T. C. (2005-06-09). "High-fidelity Z-measurement error encoding of optical qubits". Physical Review A 71 (6): 060303. doi:10.1103/PhysRevA.71.060303. Bibcode: 2005PhRvA..71f0303O. 
  8. ↑ Hayes, A. J. F.; Gilchrist, A.; Myers, C. R.; Ralph, T. C. (2004-12-01). "Utilizing encoding in scalable linear optics quantum computing". Journal of Optics B: Quantum and Semiclassical Optics (IOP Publishing) 6 (12): 533–541. doi:10.1088/1464-4266/6/12/008. ISSN 1464-4266. Bibcode: 2004JOptB...6..533H. 
  9. ↑ Pittman, T. B.; Jacobs, B. C.; Franson, J. D. (2005-05-31). "Demonstration of quantum error correction using linear optics". Physical Review A 71 (5): 052332. doi:10.1103/PhysRevA.71.052332. Bibcode: 2005PhRvA..71e2332P. 
  10. ↑ Kok, P.; Munro, W. J.; Nemoto, K.; Ralph, T. C.; Dowling, J. P.; Milburn, G. J. (2007). "Linear optical quantum computing with photonic qubits". Rev. Mod. Phys. (American Physical Society) 79 (1): 135–174. doi:10.1103/RevModPhys.79.135. Bibcode: 2007RvMP...79..135K. 
  11. ↑ Sheng, Y.-B.; Long, G. L.; Deng, F.-G. (2012). "One-step deterministic multipartite entanglement purification with linear optics". Physics Letters A 2012 (376): 314–319. doi:10.1016/j.physleta.2011.09.056. Bibcode: 2012PhLA..376..314S. https://zenodo.org/record/948907. Retrieved 2023-08-13. 



Retrieved from "https://handwiki.org/wiki/index.php?title=KLM_protocol&oldid=3361559"