Physics:Heat pump and refrigeration cycle

Thermodynamic heat pump cycles or refrigeration cycles are the conceptual and mathematical models for heat pump, air conditioning and refrigeration systems. A heat pump is a mechanical system that allows for the transmission of heat from one location (the "source") at a lower temperature to another location (the "sink" or "heat sink") at a higher temperature. Thus a heat pump may be thought of as a "heater" if the objective is to warm the heat sink (as when warming the inside of a home on a cold day), or a "refrigerator" or “cooler” if the objective is to cool the heat source (as in the normal operation of a freezer). In either case, the operating principles are similar. Heat is moved from a cold place to a warm place.

Thermodynamic cycles

According to the second law of thermodynamics, heat cannot spontaneously flow from a colder location to a hotter area; work is required to achieve this. An air conditioner requires work to cool a living space, moving heat from the interior being cooled (the heat source) to the outdoors (the heat sink). Similarly, a refrigerator moves heat from inside the cold icebox (the heat source) to the warmer room-temperature air of the kitchen (the heat sink). The operating principle of an ideal heat engine was described mathematically using the Carnot cycle by Sadi Carnot in 1824. An ideal refrigerator or heat pump can be thought of as an ideal heat engine that is operating in a reverse Carnot cycle.

Heat pump cycles and refrigeration cycles can be classified as vapor compression, vapor absorption, gas cycle, or Stirling cycle types.

Vapor-compression cycle

Vapor-compression refrigeration

For comparison, a simple stylized diagram of a heat pump's vapor-compression refrigeration cycle: 1) condenser, 2) expansion valve, 3) evaporator, 4) compressor (Note that this diagram is flipped vertically and horizontally compared to the previous one)

Temperature–entropy diagram of the vapor-compression cycle.

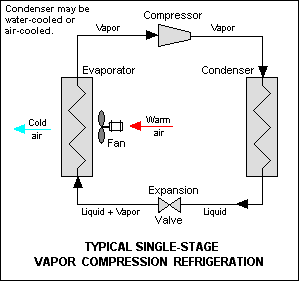
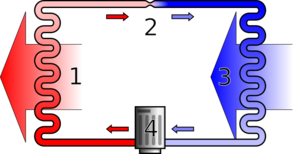
The vapor-compression cycle is used by many refrigeration, air conditioning, and other cooling applications and also within heat pump for heating applications. There are two heat exchangers, one being the condenser, which is hotter and releases heat, and the other being the evaporator, which is colder and accepts heat. For applications which need to operate in both heating and cooling modes, a reversing valve is used to switch the roles of these two heat exchangers.

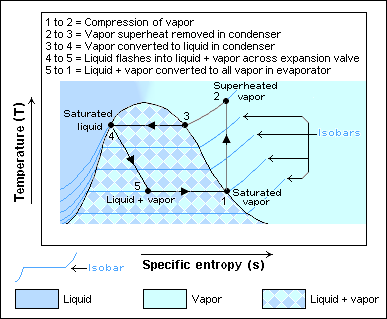
At the start of the thermodynamic cycle the refrigerant enters the compressor as a low pressure and low temperature vapor. Then the pressure is increased and the refrigerant leaves as a higher temperature and higher pressure superheated gas. This hot pressurised gas then passes through the condenser where it releases heat to the surroundings as it cools and condenses completely. The cooler high-pressure liquid next passes through the expansion valve (throttle valve) which reduces the pressure abruptly causing the temperature to drop dramatically. The cold low pressure mixture of liquid and vapor next travels through the evaporator where it vaporizes completely as it accepts heat from the surroundings before returning to the compressor as a low pressure low temperature gas to start the cycle again.

Some simpler applications with fixed operating temperatures, such as a domestic refrigerator, may use a fixed speed compressor and fixed aperture expansion valve. Applications that need to operate at a high coefficient of performance in very varied conditions, as is the case with heat pumps where external temperatures and internal heat demand vary considerably through the seasons, typically use a variable speed inverter compressor and an adjustable expansion valve to control the pressures of the cycle more accurately.

The above discussion is based on the ideal vapor-compression refrigeration cycle and does not take into account real-world effects like frictional pressure drop in the system, slight thermodynamic irreversibility during the compression of the refrigerant vapor, or non-ideal gas behavior (if any).

Vapor absorption cycle

In the early years of the twentieth century, the vapor absorption cycle using water-ammonia systems was popular and widely used but, after the development of the vapor compression cycle, it lost much of its importance because of its low coefficient of performance (about one fifth of that of the vapor compression cycle). Nowadays, the vapor absorption cycle is used only where heat is more readily available than electricity, such as industrial waste heat, solar thermal energy by solar collectors, or off-the-grid refrigeration in recreational vehicles.

The absorption cycle is similar to the compression cycle, but depends on the partial pressure of the refrigerant vapor. In the absorption system, the compressor is replaced by an absorber and a generator. The absorber dissolves the refrigerant in a suitable liquid (dilute solution) and therefore the dilute solution becomes a strong solution. In the generator, on heat addition, the temperature increases, and with it, the partial pressure of the refrigerant vapor is released from the strong solution. However, the generator requires a heat source, which would consume energy unless waste heat is used. In an absorption refrigerator, a suitable combination of refrigerant and absorbent is used. The most common combinations are ammonia (refrigerant) and water (absorbent), and water (refrigerant) and lithium bromide (absorbent).

Absorption refrigeration systems can be powered by combustion of fossil fuels (e.g., coal, oil, natural gas, etc.) or renewable energy (e.g., waste-heat recovery, biomass combustion, or solar energy).

Gas cycle

When the working fluid is a gas that is compressed and expanded but does not change phase, the refrigeration cycle is called a gas cycle. Air is most often this working fluid. As there is no condensation and evaporation intended in a gas cycle, components corresponding to the condenser and evaporator in a vapor compression cycle are the hot and cold gas-to-gas heat exchangers.

For given extreme temperatures, a gas cycle may be less efficient than a vapor compression cycle because the gas cycle works on the reverse Brayton cycle instead of the reverse Rankine cycle. As such, the working fluid never receives or rejects heat at constant temperature. In the gas cycle, the refrigeration effect is equal to the product of the specific heat of the gas and the rise in temperature of the gas in the low temperature side. Therefore, for the same cooling load, gas refrigeration cycle machines require a larger mass flow rate, which in turn increases their size.

Because of their lower efficiency and larger bulk, air cycle coolers are not often applied in terrestrial refrigeration. The air cycle machine is very common, however, on gas turbine-powered jet airliners since compressed air is readily available from the engines' compressor sections. These jet aircraft's cooling and ventilation units also serve the purpose of heating and pressurizing the aircraft cabin.

Stirling engine

The Stirling cycle heat engine can be driven in reverse, using a mechanical energy input to drive heat transfer in a reversed direction (i.e. a heat pump, or refrigerator). There are several design configurations for such devices that can be built. Several such setups require rotary or sliding seals, which can introduce difficult tradeoffs between frictional losses and refrigerant leakage.

Reversed Carnot cycle

The Carnot cycle is a reversible cycle so the four processes that comprise it, two isothermal and two isentropic, can also be reversed. When a Carnot cycle runs in reverse, it is called a reversed Carnot cycle. A refrigerator or heat pump that acts according to the reversed Carnot cycle is called a Carnot refrigerator or Carnot heat pump, respectively. In the first stage of this cycle, the refrigerant absorbs heat isothermally from a low-temperature source, T_L, in the amount Q_L. Next, the refrigerant is compressed isentropically (adiabatically, without heat transfer) and its temperature rises to that of the high-temperature source, T_H. Then at this high temperature, the refrigerant isothermally rejects heat in the amount Q_H < 0 (negative according to the sign convention for heat lost by the system). Also during this stage, the refrigerant changes from a saturated vapor to a saturated liquid in the condenser. Lastly, the refrigerant expands isentropically until its temperature falls to that of the low-temperature source, T_L.

Coefficient of performance

The merit of a refrigerator or heat pump is given by a parameter called the coefficient of performance (COP). The equation is:

[math]\displaystyle{ {\rm COP} = \frac{|Q|}{ W_{net,in}} }[/math]

where

• [math]\displaystyle{ Q }[/math] is the useful heat given off or taken up by the considered system.
• [math]\displaystyle{ W_{net,in} }[/math] is the net work done on the considered system in one cycle.

The detailed COP of a refrigerator is given by the following equation:

[math]\displaystyle{ {\rm COP_R} = \frac{ \text{Desired Output}}{ \text{Required Input}} = \frac{ \text{Cooling Effect}}{ \text{Work Input}} = \frac{ Q_L}{ W_\text{net,in} } }[/math]

The COP of a heat pump (sometimes referred to as coefficient of amplification COA) is given by the following equations, where the first law of thermodynamics: [math]\displaystyle{ W_{net,in}+Q_{L}+Q_{H} = \Delta_{cycle}U = 0 }[/math] and [math]\displaystyle{ |Q_{H}|= -Q_{H} }[/math] was used in one of the last steps:

[math]\displaystyle{ {\rm COP_{HP} } = \frac{ \text{Desired Output}} { \text{Required Input}} = \frac{ \text{Heating Effect}} { \text{Work Input}} = \frac{|Q_H|} { W_\text{net,in} }= \frac{W_{net,in} + Q_L} { W_\text{net,in} }=1 +\frac { Q_L} { W_\text{net,in} } }[/math]

Both the COP of a refrigerator and a heat pump can be greater than one. Combining these two equations results in:

[math]\displaystyle{ {\rm COP_{HP} } = 1+{\rm COP_R } }[/math] for fixed values of Q_H and Q_L.

This implies that COP_HP will be greater than one because COP_R will be a positive quantity. In a worst-case scenario, the heat pump will supply as much energy as it consumes, making it act as a resistance heater. However, in reality, as in home heating, some of Q_H is lost to the outside air through piping, insulation, etc., thus making the COP_HP drop below unity when the outside air temperature is too low. Therefore, the system used to heat houses uses fuel.

For Carnot refrigerators and heat pumps, the COP can be expressed in terms of temperatures:

[math]\displaystyle{ {\rm COP_{R,Carnot} } = \frac { T_L} { T_H - T_L} = \frac { 1} { (T_H / T_L) - 1} }[/math]

[math]\displaystyle{ {\rm COP_{HP,Carnot} } = \frac { T_H} { T_H-T_L} = \frac { 1} { 1 - (T_L / T_H)} }[/math]

These are the upper limits for the COP of any system operating between T_L and T_H.

References

Notes

• Turns, Stephen (2006). Thermodynamics: Concepts and Applications. Cambridge University Press. pp. 756. ISBN 0-521-85042-8. https://books.google.com/books?id=fy5hs04OeMQC&q=Heat+pump+and+refrigeration+cycle. 
• Dincer, Ibrahim (2003). Refrigeration Systems and Applications. John Wiley and Sons. pp. 598. ISBN 0-471-62351-2. 
• Whitman, Bill (2008). Refrigeration and Air conditioning Technology. Delmar. 

External links

• "The Basic Refrigeration Cycle"