Physics:Bremsstrahlung

Short description: Electromagnetic radiation due to deceleration of charged particles

Bremsstrahlung produced by a high-energy electron deflected in the electric field of an atomic nucleus.

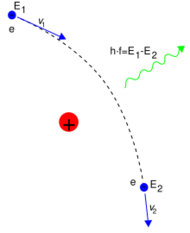
In particle physics, bremsstrahlung /ˈbrɛmʃtrɑːləŋ/ (German pronunciation: [ˈbʁɛms.ʃtʁaːlʊŋ] (listen); from de bremsen 'to brake', and Strahlung 'radiation') is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation (i.e., photons), thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

Broadly speaking, bremsstrahlung or braking radiation is any radiation produced due to the acceleration (positive or negative) of a charged particle, which includes synchrotron radiation (i.e., photon emission by a relativistic particle), cyclotron radiation (i.e. photon emission by a non-relativistic particle), and the emission of electrons and positrons during beta decay. However, the term is frequently used in the more narrow sense of radiation from electrons (from whatever source) slowing in matter.

Bremsstrahlung emitted from plasma is sometimes referred to as free–free radiation. This refers to the fact that the radiation in this case is created by electrons that are free (i.e., not in an atomic or molecular bound state) before, and remain free after, the emission of a photon. In the same parlance, bound–bound radiation refers to discrete spectral lines (an electron "jumps" between two bound states), while free–bound radiation refers to the radiative combination process, in which a free electron recombines with an ion.

Classical description

Field lines and modulus of the electric field generated by a (negative) charge first moving at a constant speed and then stopping quickly to show the generated Bremsstrahlung radiation.

If quantum effects are negligible, an accelerating charged particle radiates power as described by the Larmor formula and its relativistic generalization.

Total radiated power

The total radiated power is [math]\displaystyle{ P = \frac{q^2 \gamma^4}{6 \pi \varepsilon_0 c} \left( \dot{\beta}^2 + \frac{\left(\boldsymbol{\beta} \cdot \dot{\boldsymbol{\beta}}\right)^2}{1 - \beta^2}\right), }[/math] where [math]\displaystyle{ \boldsymbol\beta = \frac{\mathbf v}{c} }[/math] (the velocity of the particle divided by the speed of light), [math]\displaystyle{ \gamma = {1}/{\sqrt{1-\beta^2}} }[/math] is the Lorentz factor, [math]\displaystyle{ \varepsilon_0 }[/math] is the vacuum permittivity, [math]\displaystyle{ \dot{\boldsymbol\beta} }[/math] signifies a time derivative of [math]\displaystyle{ \boldsymbol\beta }[/math], and q is the charge of the particle. In the case where velocity is parallel to acceleration (i.e., linear motion), the expression reduces to [math]\displaystyle{ P_{a \parallel v} = \frac{q^2 a^2 \gamma^6}{6 \pi \varepsilon_0 c^3}, }[/math] where [math]\displaystyle{ a \equiv \dot{v} = \dot{\beta}c }[/math] is the acceleration. For the case of acceleration perpendicular to the velocity ([math]\displaystyle{ \boldsymbol{\beta} \cdot \dot{\boldsymbol{\beta}} = 0 }[/math]), for example in synchrotrons, the total power is [math]\displaystyle{ P_{a \perp v} = \frac{q^2 a^2 \gamma^4 }{6 \pi \varepsilon_0 c^3}. }[/math]

Power radiated in the two limiting cases is proportional to [math]\displaystyle{ \gamma^4 }[/math] [math]\displaystyle{ \left(a \perp v\right) }[/math] or [math]\displaystyle{ \gamma^6 }[/math] [math]\displaystyle{ \left(a \parallel v\right) }[/math]. Since [math]\displaystyle{ E = \gamma m c^2 }[/math], we see that for particles with the same energy [math]\displaystyle{ E }[/math] the total radiated power goes as [math]\displaystyle{ m^{-4} }[/math] or [math]\displaystyle{ m^{-6} }[/math], which accounts for why electrons lose energy to bremsstrahlung radiation much more rapidly than heavier charged particles (e.g., muons, protons, alpha particles). This is the reason a TeV energy electron-positron collider (such as the proposed International Linear Collider) cannot use a circular tunnel (requiring constant acceleration), while a proton-proton collider (such as the Large Hadron Collider) can utilize a circular tunnel. The electrons lose energy due to bremsstrahlung at a rate [math]\displaystyle{ (m_p/m_e)^4 \approx 10^{13} }[/math] times higher than protons do.

Angular distribution

The most general formula for radiated power as a function of angle is: [math]\displaystyle{ \frac{d P}{d\Omega} = \frac{q^2}{16\pi^2 \varepsilon_0 c} \frac{\left|\hat{\mathbf n} \times \left(\left(\hat{\mathbf n} - \boldsymbol{\beta}\right) \times \dot{\boldsymbol{\beta}}\right)\right|^2}{\left(1 - \hat{\mathbf n}\cdot\boldsymbol{\beta}\right)^5} }[/math] where [math]\displaystyle{ \hat{\mathbf n} }[/math] is a unit vector pointing from the particle towards the observer, and [math]\displaystyle{ d\Omega }[/math] is an infinitesimal bit of solid angle.

In the case where velocity is parallel to acceleration (for example, linear motion), this simplifies to [math]\displaystyle{ \frac{dP_{a \parallel v}}{d\Omega} = \frac{q^2a^2}{16\pi^2 \varepsilon_0 c^3}\frac{\sin^2 \theta}{(1 - \beta \cos\theta)^5} }[/math] where [math]\displaystyle{ \theta }[/math] is the angle between [math]\displaystyle{ \boldsymbol{\beta} }[/math] and the direction of observation [math]\displaystyle{ \hat{\mathbf n} }[/math].

Simplified quantum-mechanical description

The full quantum-mechanical treatment of bremsstrahlung is very involved. The "vacuum case" of the interaction of one electron, one ion, and one photon, using the pure Coulomb potential, has an exact solution that was probably first published by A. Sommerfeld in 1931. This analytical solution involves complicated mathematics, and several numerical calculations have been published, such as by Karzas and Latter. Other approximate formulas have been presented, such as in recent work by Weinberg and Pradler and Semmelrock.

This section gives a quantum-mechanical analog of the prior section, but with some simplifications to illustrate the important physics. We give a non-relativistic treatment of the special case of an electron of mass [math]\displaystyle{ m_e }[/math], charge [math]\displaystyle{ -e }[/math], and initial speed [math]\displaystyle{ v }[/math] decelerating in the Coulomb field of a gas of heavy ions of charge [math]\displaystyle{ Ze }[/math] and number density [math]\displaystyle{ n_i }[/math]. The emitted radiation is a photon of frequency [math]\displaystyle{ \nu=c/\lambda }[/math] and energy [math]\displaystyle{ h\nu }[/math]. We wish to find the emissivity [math]\displaystyle{ j(v,\nu) }[/math] which is the power emitted per (solid angle in photon velocity space * photon frequency), summed over both transverse photon polarizations. We express it as an approximate classical result times the free−free emission Gaunt factor g_ff accounting for quantum and other corrections: [math]\displaystyle{ j(v,\nu) = {8\pi\over 3\sqrt3}\left({e^2\over 4\pi\epsilon_0}\right)^3 {Z^2n_i \over c^3m_e^2v}g_{\rm ff}(v,\nu) }[/math] [math]\displaystyle{ j(\nu,v) = 0 }[/math] if [math]\displaystyle{ h\nu \gt mv^2/2 }[/math], that is, the electron does not have enough kinetic energy to emit the photon. A general, quantum-mechanical formula for [math]\displaystyle{ g_{\rm ff} }[/math] exists but is very complicated, and usually is found by numerical calculations. We present some approximate results with the following additional assumptions:

• Vacuum interaction: we neglect any effects of the background medium, such as plasma screening effects. This is reasonable for photon frequency much greater than the plasma frequency [math]\displaystyle{ \nu_{\rm pe} \propto n_{\rm e}^{1/2} }[/math]with [math]\displaystyle{ n_e }[/math] the plasma electron density. Note that light waves are evanescent for [math]\displaystyle{ \nu\lt \nu_{\rm pe} }[/math] and a significantly different approach would be needed.
• Soft photons: [math]\displaystyle{ h\nu\ll m_ev^2/2 }[/math], that is, the photon energy is much less than the initial electron kinetic energy.

With these assumptions, two unitless parameters characterize the process: [math]\displaystyle{ \eta_Z \equiv Ze^2/\hbar v }[/math], which measures the strength of the electron-ion Coulomb interaction, and [math]\displaystyle{ \eta_\nu \equiv h\nu/2m_ev^2 }[/math], which measures the photon "softness" and we assume is always small (the choice of the factor 2 is for later convenience). In the limit [math]\displaystyle{ \eta_Z\ll 1 }[/math], the quantum-mechanical Born approximation gives: [math]\displaystyle{ g_\text{ff,Born} = {\sqrt3 \over \pi}\ln{1\over\eta_\nu} }[/math]

In the opposite limit [math]\displaystyle{ \eta_Z\gg 1 }[/math], the full quantum-mechanical result reduces to the purely classical result [math]\displaystyle{ g_\text{ff,class} = {\sqrt3\over\pi}\left[\ln\left({1\over \eta_Z\eta_\nu}\right)- \gamma \right] }[/math] where [math]\displaystyle{ \gamma\approx 0.577 }[/math] is the Euler–Mascheroni constant. Note that [math]\displaystyle{ 1/\eta_Z\eta_\nu=m_ev^3/\pi Ze^2\nu }[/math] which is a purely classical expression without Planck's constant [math]\displaystyle{ h }[/math].

A semi-classical, heuristic way to understand the Gaunt factor is to write it as [math]\displaystyle{ g_\text{ff} \approx \ln(b_\text{max}/b_\text{min}) }[/math] where [math]\displaystyle{ b_{\max} }[/math] and [math]\displaystyle{ b_{\min} }[/math] are maximum and minimum "impact parameters" for the electron-ion collision, in the presence of the photon electric field. With our assumptions, [math]\displaystyle{ b_{\rm max}=v/\nu }[/math]: for larger impact parameters, the sinusoidal oscillation of the photon field provides "phase mixing" that strongly reduces the interaction. [math]\displaystyle{ b_{\rm min} }[/math] is the larger of the quantum-mechanical de Broglie wavelength [math]\displaystyle{ \approx h/m_e v }[/math] and the classical distance of closest approach [math]\displaystyle{ \approx e^2 / 4\pi \varepsilon_0 m_e v^2 }[/math] where the electron-ion Coulomb potential energy is comparable to the electron's initial kinetic energy.

The above approximations generally apply as long as the argument of the logarithm is large, and break down when it is less than unity. Namely, these forms for the Gaunt factor become negative, which is unphysical. A rough approximation to the full calculations, with the appropriate Born and classical limits, is [math]\displaystyle{ g_\text{ff} \approx \max\left[1, {\sqrt3\over\pi} \ln\left[{1\over \eta_\nu\max(1,e^\gamma\eta_Z)}\right] \right] }[/math]

Thermal bremsstrahlung in a medium: emission and absorption

The bremsstrahlung power spectrum rapidly decreases for large [math]\displaystyle{ \omega }[/math], and is also suppressed near [math]\displaystyle{ \omega = \omega_{\rm p} }[/math]. This plot is for the quantum case [math]\displaystyle{ T_e \gt Z^2 E_\text{h} }[/math], and [math]\displaystyle{ \hbar \omega_\text{p} / T_e = 0.1 }[/math].

This section discusses bremsstrahlung emission and the inverse absorption process (called inverse bremsstrahlung) in a macroscopic medium. We start with the equation of radiative transfer, which applies to general processes and not just bremsstrahlung: [math]\displaystyle{ \frac{1}{c} \partial_t I_\nu + \hat \mathbf n\cdot\nabla I_\nu = j_\nu-k_\nu I_\nu }[/math]

[math]\displaystyle{ I_\nu(t,\mathbf x) }[/math] is the radiation spectral intensity, or power per (area × solid angle in photon velocity space × photon frequency) summed over both polarizations. [math]\displaystyle{ j_\nu }[/math] is the emissivity, analogous to [math]\displaystyle{ j(v,\nu) }[/math]defined above, and [math]\displaystyle{ k_\nu }[/math] is the absorptivity. [math]\displaystyle{ j_\nu }[/math] and [math]\displaystyle{ k_\nu }[/math] are properties of the matter, not the radiation, and account for all the particles in the medium - not just a pair of one electron and one ion as in the prior section. If [math]\displaystyle{ I_\nu }[/math] is uniform in space and time, then the left-hand side of the transfer equation is zero, and we find

[math]\displaystyle{ I_\nu={j_\nu \over k_\nu} }[/math]

If the matter and radiation are also in thermal equilibrium at some temperature, then [math]\displaystyle{ I_\nu }[/math] must be the blackbody spectrum:

[math]\displaystyle{ B_\nu(\nu, T_e) = \frac{2h\nu^3}{c^2}\frac{1}{e^{h\nu/k_\text{B}T_e} - 1} }[/math]

Since [math]\displaystyle{ j_\nu }[/math] and [math]\displaystyle{ k_\nu }[/math] are independent of [math]\displaystyle{ I_\nu }[/math], this means that [math]\displaystyle{ j_\nu/k_\nu }[/math] must be the blackbody spectrum whenever the matter is in equilibrium at some temperature – regardless of the state of the radiation. This allows us to immediately know both [math]\displaystyle{ j_\nu }[/math] and [math]\displaystyle{ k_\nu }[/math] once one is known – for matter in equilibrium.

In plasma

NOTE: this section currently gives formulas that apply in the Rayleigh–Jeans limit [math]\displaystyle{ \hbar \omega \ll k_\text{B} T_e }[/math], and does not use a quantized (Planck) treatment of radiation. Thus a usual factor like [math]\displaystyle{ \exp(-\hbar\omega/k_{\rm B}T_e) }[/math] does not appear. The appearance of [math]\displaystyle{ \hbar \omega / k_\text{B} T_e }[/math] in [math]\displaystyle{ y }[/math] below is due to the quantum-mechanical treatment of collisions.

In a plasma, the free electrons continually collide with the ions, producing bremsstrahlung. A complete analysis requires accounting for both binary Coulomb collisions as well as collective (dielectric) behavior. A detailed treatment is given by Bekefi, while a simplified one is given by Ichimaru. In this section we follow Bekefi's dielectric treatment, with collisions included approximately via the cutoff wavenumber, [math]\displaystyle{ k_\text{max} }[/math].

Consider a uniform plasma, with thermal electrons distributed according to the Maxwell–Boltzmann distribution with the temperature [math]\displaystyle{ T_e }[/math]. Following Bekefi, the power spectral density (power per angular frequency interval per volume, integrated over the whole [math]\displaystyle{ 4\pi }[/math] sr of solid angle, and in both polarizations) of the bremsstrahlung radiated, is calculated to be [math]\displaystyle{ {dP_\mathrm{Br} \over d\omega} = \frac{8\sqrt 2}{3\sqrt\pi} \left[\frac{e^2}{4\pi\varepsilon_0} \right]^3 {1 \over (m_e c^2)^{3/2}} \left[1-{\omega_{\rm p}^2 \over \omega^2}\right]^{1/2} {Z_i^2 n_i n_e \over (k_{\rm B} T_e)^{1/2}} E_1(y), }[/math] where [math]\displaystyle{ \omega_p \equiv (n_ee^2/\varepsilon_0m_e)^{1/2} }[/math] is the electron plasma frequency, [math]\displaystyle{ \omega }[/math] is the photon frequency, [math]\displaystyle{ n_e, n_i }[/math] is the number density of electrons and ions, and other symbols are physical constants. The second bracketed factor is the index of refraction of a light wave in a plasma, and shows that emission is greatly suppressed for [math]\displaystyle{ \omega \lt \omega_{\rm p} }[/math] (this is the cutoff condition for a light wave in a plasma; in this case the light wave is evanescent). This formula thus only applies for [math]\displaystyle{ \omega\gt \omega_{\rm p} }[/math]. This formula should be summed over ion species in a multi-species plasma.

The special function [math]\displaystyle{ E_1 }[/math] is defined in the exponential integral article, and the unitless quantity [math]\displaystyle{ y }[/math] is [math]\displaystyle{ y = \frac{1}{2} {\omega^2 m_e \over k_\text{max}^2 k_\text{B} T_e} }[/math]

[math]\displaystyle{ k_\text{max} }[/math] is a maximum or cutoff wavenumber, arising due to binary collisions, and can vary with ion species. Roughly, [math]\displaystyle{ k_\text{max} = 1 / \lambda_\text{B} }[/math] when [math]\displaystyle{ k_\text{B} T_\text{e} \gt Z_i^2 E_\text{h} }[/math] (typical in plasmas that are not too cold), where [math]\displaystyle{ E_\text{h} \approx 27.2 }[/math] eV is the Hartree energy, and [math]\displaystyle{ \lambda_\text{B} = \hbar / (m_\text{e} k_\text{B} T_\text{e})^{1/2} }[/math] is the electron thermal de Broglie wavelength. Otherwise, [math]\displaystyle{ k_\text{max} \propto 1/l_\text{C} }[/math] where [math]\displaystyle{ l_\text{C} }[/math] is the classical Coulomb distance of closest approach.

For the usual case [math]\displaystyle{ k_m = 1/\lambda_B }[/math], we find [math]\displaystyle{ y = \frac{1}{2} \left[\frac{\hbar\omega}{k_\text{B} T_e}\right]^2. }[/math]

The formula for [math]\displaystyle{ dP_\mathrm{Br} / d\omega }[/math] is approximate, in that it neglects enhanced emission occurring for [math]\displaystyle{ \omega }[/math] slightly above [math]\displaystyle{ \omega_\text{p} }[/math].

In the limit [math]\displaystyle{ y\ll 1 }[/math], we can approximate [math]\displaystyle{ E_1 }[/math] as [math]\displaystyle{ E_1(y) \approx -\ln [y e^\gamma] + O(y) }[/math] where [math]\displaystyle{ \gamma \approx 0.577 }[/math] is the Euler–Mascheroni constant. The leading, logarithmic term is frequently used, and resembles the Coulomb logarithm that occurs in other collisional plasma calculations. For [math]\displaystyle{ y \gt e^{-\gamma} }[/math] the log term is negative, and the approximation is clearly inadequate. Bekefi gives corrected expressions for the logarithmic term that match detailed binary-collision calculations.

The total emission power density, integrated over all frequencies, is [math]\displaystyle{ \begin{align} P_\mathrm{Br} &= \int_{\omega_\text{p}}^\infty d\omega \frac{dP_\mathrm{Br}}{d\omega} = \frac{16}{3} \left[ \frac{e^2}{4\pi\varepsilon_0} \right]^3 \frac{1}{m_e^2 c^3} Z_i^2 n_i n_e k_\text{max} G(y_\text{p}) \\[1ex] G(y_p) &= \frac{1}{2\sqrt{\pi}} \int_{y_\text{p}}^\infty dy \, y^{-{1}/{2}} \left[1 - {y_\text{p} \over y}\right]^{1/2} E_1(y) \\[1ex] y_\text{p} &= y({\omega\!=\!\omega_\text{p}}) \end{align} }[/math]

[math]\displaystyle{ G(y_\text{p}=0) = 1 }[/math] and decreases with [math]\displaystyle{ y_\text{p} }[/math]; it is always positive. For [math]\displaystyle{ k_\text{max} = 1/\lambda_\text{B} }[/math], we find

[math]\displaystyle{ P_\mathrm{Br} = {16 \over 3} {\left(\frac{e^2}{4\pi\varepsilon_0}\right)^3 \over (m_e c^2)^\frac{3}{2}\hbar} Z_i^2 n_i n_e (k_{\rm B} T_e)^\frac{1}{2} G(y_{\rm p}) }[/math]

Note the appearance of [math]\displaystyle{ \hbar }[/math] due to the quantum nature of [math]\displaystyle{ \lambda_{\rm B} }[/math]. In practical units, a commonly used version of this formula for [math]\displaystyle{ G=1 }[/math] is [math]\displaystyle{ P_\mathrm{Br} [\mathrm{W/m^3}] = {Z_i^2 n_i n_e \over \left[7.69 \times 10^{18} \mathrm{m^{-3}}\right]^2} T_e[\mathrm{eV}]^\frac{1}{2}. }[/math]

This formula is 1.59 times the one given above, with the difference due to details of binary collisions. Such ambiguity is often expressed by introducing Gaunt factor [math]\displaystyle{ g_{\rm B} }[/math], e.g. in one finds [math]\displaystyle{ \varepsilon_\text{ff} = 1.4\times 10^{-27} T^\frac{1}{2} n_e n_i Z^2 g_\text{B},\, }[/math] where everything is expressed in the CGS units.

Relativistic corrections

Relativistic corrections to the emission of a 30-keV photon by an electron impacting on a proton.

For very high temperatures there are relativistic corrections to this formula, that is, additional terms of the order of [math]\displaystyle{ k_\text{B} T_e/m_e c^2 }[/math].

Bremsstrahlung cooling

If the plasma is optically thin, the bremsstrahlung radiation leaves the plasma, carrying part of the internal plasma energy. This effect is known as the bremsstrahlung cooling. It is a type of radiative cooling. The energy carried away by bremsstrahlung is called bremsstrahlung losses and represents a type of radiative losses. One generally uses the term bremsstrahlung losses in the context when the plasma cooling is undesired, as e.g. in fusion plasmas.

Polarizational bremsstrahlung

Polarizational bremsstrahlung (sometimes referred to as "atomic bremsstrahlung") is the radiation emitted by the target's atomic electrons as the target atom is polarized by the Coulomb field of the incident charged particle. Polarizational bremsstrahlung contributions to the total bremsstrahlung spectrum have been observed in experiments involving relatively massive incident particles, resonance processes, and free atoms. However, there is still some debate as to whether or not there are significant polarizational bremsstrahlung contributions in experiments involving fast electrons incident on solid targets.

It is worth noting that the term "polarizational" is not meant to imply that the emitted bremsstrahlung is polarized. Also, the angular distribution of polarizational bremsstrahlung is theoretically quite different than ordinary bremsstrahlung.

Sources

X-ray tube

Spectrum of the X-rays emitted by an X-ray tube with a rhodium target, operated at 60 kV. The continuous curve is due to bremsstrahlung, and the spikes are characteristic K lines for rhodium. The curve goes to zero at 21 pm in agreement with the Duane–Hunt law, as described in the text.

In an X-ray tube, electrons are accelerated in a vacuum by an electric field towards a piece of metal called the "target". X-rays are emitted as the electrons slow down (decelerate) in the metal. The output spectrum consists of a continuous spectrum of X-rays, with additional sharp peaks at certain energies. The continuous spectrum is due to bremsstrahlung, while the sharp peaks are characteristic X-rays associated with the atoms in the target. For this reason, bremsstrahlung in this context is also called continuous X-rays.

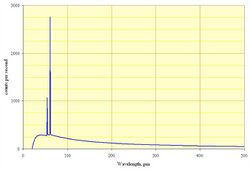
The shape of this continuum spectrum is approximately described by Kramers' law.

The formula for Kramers' law is usually given as the distribution of intensity (photon count) [math]\displaystyle{ I }[/math] against the wavelength [math]\displaystyle{ \lambda }[/math] of the emitted radiation: [math]\displaystyle{ I(\lambda) \, d\lambda = K \left( \frac{\lambda}{\lambda_{\min}} - 1 \right)\frac{d\lambda}{\lambda^2} }[/math]

The constant K is proportional to the atomic number of the target element, and [math]\displaystyle{ \lambda_{\min} }[/math] is the minimum wavelength given by the Duane–Hunt law.

The spectrum has a sharp cutoff at [math]\displaystyle{ \lambda_{\min} }[/math], which is due to the limited energy of the incoming electrons. For example, if an electron in the tube is accelerated through 60 kV, then it will acquire a kinetic energy of 60 keV, and when it strikes the target it can create X-rays with energy of at most 60 keV, by conservation of energy. (This upper limit corresponds to the electron coming to a stop by emitting just one X-ray photon. Usually the electron emits many photons, and each has an energy less than 60 keV.) A photon with energy of at most 60 keV has wavelength of at least 21 pm, so the continuous X-ray spectrum has exactly that cutoff, as seen in the graph. More generally the formula for the low-wavelength cutoff, the Duane–Hunt law, is: [math]\displaystyle{ \lambda_\min = \frac{h c}{e V} \approx \frac{1239.8}{V}\,\mathrm{pm/kV} }[/math] where h is Planck's constant, c is the speed of light, V is the voltage that the electrons are accelerated through, e is the elementary charge, and pm is picometres.

Beta decay

Beta particle-emitting substances sometimes exhibit a weak radiation with continuous spectrum that is due to bremsstrahlung (see the "outer bremsstrahlung" below). In this context, bremsstrahlung is a type of "secondary radiation", in that it is produced as a result of stopping (or slowing) the primary radiation (beta particles). It is very similar to X-rays produced by bombarding metal targets with electrons in X-ray generators (as above) except that it is produced by high-speed electrons from beta radiation.

Inner and outer bremsstrahlung

The "inner" bremsstrahlung (also known as "internal bremsstrahlung") arises from the creation of the electron and its loss of energy (due to the strong electric field in the region of the nucleus undergoing decay) as it leaves the nucleus. Such radiation is a feature of beta decay in nuclei, but it is occasionally (less commonly) seen in the beta decay of free neutrons to protons, where it is created as the beta electron leaves the proton.

In electron and positron emission by beta decay the photon's energy comes from the electron-nucleon pair, with the spectrum of the bremsstrahlung decreasing continuously with increasing energy of the beta particle. In electron capture, the energy comes at the expense of the neutrino, and the spectrum is greatest at about one third of the normal neutrino energy, decreasing to zero electromagnetic energy at normal neutrino energy. Note that in the case of electron capture, bremsstrahlung is emitted even though no charged particle is emitted. Instead, the bremsstrahlung radiation may be thought of as being created as the captured electron is accelerated toward being absorbed. Such radiation may be at frequencies that are the same as soft gamma radiation, but it exhibits none of the sharp spectral lines of gamma decay, and thus is not technically gamma radiation.

The internal process is to be contrasted with the "outer" bremsstrahlung due to the impingement on the nucleus of electrons coming from the outside (i.e., emitted by another nucleus), as discussed above.

Radiation safety

In some cases, such as the decay of ³²P, the bremsstrahlung produced by shielding the beta radiation with the normally used dense materials (e.g. lead) is itself dangerous; in such cases, shielding must be accomplished with low density materials, such as Plexiglas (Lucite), plastic, wood, or water; as the atomic number is lower for these materials, the intensity of bremsstrahlung is significantly reduced, but a larger thickness of shielding is required to stop the electrons (beta radiation).

In astrophysics

The dominant luminous component in a cluster of galaxies is the 10⁷ to 10⁸ kelvin intracluster medium. The emission from the intracluster medium is characterized by thermal bremsstrahlung. This radiation is in the energy range of X-rays and can be easily observed with space-based telescopes such as Chandra X-ray Observatory, XMM-Newton, ROSAT, ASCA, EXOSAT, Suzaku, RHESSI and future missions like IXO [1] and Astro-H [2].

Bremsstrahlung is also the dominant emission mechanism for H II regions at radio wavelengths.

In electric discharges

In electric discharges, for example as laboratory discharges between two electrodes or as lightning discharges between cloud and ground or within clouds, electrons produce Bremsstrahlung photons while scattering off air molecules. These photons become manifest in terrestrial gamma-ray flashes and are the source for beams of electrons, positrons, neutrons and protons. The appearance of Bremsstrahlung photons also influences the propagation and morphology of discharges in nitrogen-oxygen mixtures with low percentages of oxygen.

Quantum mechanical description

The complete quantum mechanical description was first performed by Bethe and Heitler. They assumed plane waves for electrons which scatter at the nucleus of an atom, and derived a cross section which relates the complete geometry of that process to the frequency of the emitted photon. The quadruply differential cross section, which shows a quantum mechanical symmetry to pair production, is

[math]\displaystyle{ \begin{align} d^4\sigma ={} &\frac{Z^2 \alpha_\text{fine}^3 \hbar^2}{(2\pi)^2}\frac{\left|\mathbf{p}_f\right|}{\left|\mathbf{p}_i\right|} \frac{d\omega}{\omega}\frac{d\Omega_i \, d\Omega_f \, d\Phi}{\left|\mathbf{q}\right|^4} \\ &{}\times \left[ \frac{\mathbf{p}_f^2\sin^2\Theta_f}{\left(E_f - c\left|\mathbf{p}_f\right| \cos\Theta_f\right)^2}\left(4E_i^2 - c^2\mathbf{q}^2\right) + \frac{\mathbf{p}_i^2\sin^2\Theta_i}{\left(E_i - c\left|\mathbf{p}_i\right| \cos\Theta_i\right)^2}\left(4E_f^2 - c^2\mathbf{q}^2\right) \right. \\ & {} \qquad+ 2\hbar^2\omega^2 \frac {\mathbf{p}_i^2 \sin^2\Theta_i + \mathbf{p}_f^2 \sin^2\Theta_f} {(E_f - c\left|\mathbf{p}_f\right| \cos\Theta_f)\left(E_i - c\left|\mathbf{p}_i\right| \cos\Theta_i\right)} \\ & {} \qquad- 2\left. \frac {\left|\mathbf{p}_i\right| \left|\mathbf{p}_f\right| \sin\Theta_i \sin\Theta_f \cos\Phi} {\left(E_f - c\left|\mathbf{p}_f\right| \cos\Theta_f\right)\left(E_i - c\left|\mathbf{p}_i\right| c1\cos\Theta_i\right)} \left(2E_i^2 + 2E_f^2 - c^2\mathbf{q}^2\right) \right], \end{align} }[/math]

where [math]\displaystyle{ Z }[/math] is the atomic number, [math]\displaystyle{ \alpha_\text{fine}\approx 1/137 }[/math] the fine-structure constant, [math]\displaystyle{ \hbar }[/math] the reduced Planck's constant and [math]\displaystyle{ c }[/math] the speed of light. The kinetic energy [math]\displaystyle{ E_{\text{kin},i/f} }[/math] of the electron in the initial and final state is connected to its total energy [math]\displaystyle{ E_{i,f} }[/math] or its momenta [math]\displaystyle{ \mathbf{p}_{i,f} }[/math] via [math]\displaystyle{ E_{i, f} = E_{\text{kin}, i/f} + m_e c^2 = \sqrt{m_e^2 c^4 + \mathbf{p}_{i, f}^2 c^2}, }[/math] where [math]\displaystyle{ m_e }[/math] is the mass of an electron. Conservation of energy gives [math]\displaystyle{ E_f = E_i - \hbar\omega, }[/math] where [math]\displaystyle{ \hbar\omega }[/math] is the photon energy. The directions of the emitted photon and the scattered electron are given by [math]\displaystyle{ \begin{align} \Theta_i &= \sphericalangle(\mathbf{p}_i, \mathbf{k}),\\ \Theta_f &= \sphericalangle(\mathbf{p}_f, \mathbf{k}),\\ \Phi &= \text{Angle between the planes } (\mathbf{p}_i, \mathbf{k}) \text{ and } (\mathbf{p}_f, \mathbf{k}), \end{align} }[/math] where [math]\displaystyle{ \mathbf{k} }[/math] is the momentum of the photon.

The differentials are given as [math]\displaystyle{ \begin{align} d\Omega_i &= \sin\Theta_i\ d\Theta_i,\\ d\Omega_f &= \sin\Theta_f\ d\Theta_f. \end{align} }[/math]

The absolute value of the virtual photon between the nucleus and electron is

[math]\displaystyle{ \begin{align} -\mathbf{q}^2 ={} & -\left|\mathbf{p}_i\right|^2 - \left|\mathbf{p}_f\right|^2 - \left(\frac{\hbar}{c}\omega\right)^2 + 2\left|\mathbf{p}_i\right|\frac{\hbar}{c} \omega\cos\Theta_i - 2\left|\mathbf{p}_f\right|\frac{\hbar}{c} \omega\cos\Theta_f \\ & {} + 2\left|\mathbf{p}_i\right| \left|\mathbf{p}_f\right| \left(\cos\Theta_f\cos\Theta_i + \sin\Theta_f\sin\Theta_i\cos\Phi\right). \end{align} }[/math]

The range of validity is given by the Born approximation [math]\displaystyle{ v \gg \frac{Zc}{137} }[/math] where this relation has to be fulfilled for the velocity [math]\displaystyle{ v }[/math] of the electron in the initial and final state.

For practical applications (e.g. in Monte Carlo codes) it can be interesting to focus on the relation between the frequency [math]\displaystyle{ \omega }[/math] of the emitted photon and the angle between this photon and the incident electron. Köhn and Ebert integrated the quadruply differential cross section by Bethe and Heitler over [math]\displaystyle{ \Phi }[/math] and [math]\displaystyle{ \Theta_f }[/math] and obtained: [math]\displaystyle{ \frac{d^2\sigma (E_i, \omega, \Theta_i)}{d\omega \, d\Omega_i} = \sum\limits_{j=1}^6 I_j }[/math]

with

[math]\displaystyle{ \begin{align} I_1 ={} &\frac{2\pi A}{\sqrt{\Delta_2^2 + 4p_i^2 p_f^2 \sin^2\Theta_i}} \ln\left(\frac { \Delta_2^2 + 4p_i^2p_f^2\sin^2\Theta_i - \sqrt{\Delta_2^2 + 4p_i^2p_f^2\sin^2\Theta_i}\left(\Delta_1 + \Delta_2\right) + \Delta_1\Delta_2} {-\Delta_2^2 - 4p_i^2p_f^2\sin^2\Theta_i - \sqrt{\Delta_2^2 + 4p_i^2p_f^2\sin^2\Theta_i}\left(\Delta_1 - \Delta_2\right) + \Delta_1\Delta_2} \right) \\ & {} \times\left[ 1 + \frac{c\Delta_2}{p_f\left(E_i - cp_i\cos\Theta_i\right)} - \frac{p_i^2 c^2 \sin^2\Theta_i}{\left(E_i - cp_i\cos\Theta_i\right)^2} - \frac{2\hbar^2\omega^2 p_f \Delta_2}{c\left(E_i - cp_i\cos\Theta_i\right)\left(\Delta_2^2 + 4p_i^2 p_f^2 \sin^2\Theta_i\right)} \right], \\ I_2 ={} &-\frac{2\pi Ac}{p_f\left(E_i - cp_i\cos\Theta_i\right)}\ln\left(\frac{E_f + p_fc}{E_f - p_fc}\right), \\ I_3 = {} & \frac{2\pi A}{\sqrt{\left(\Delta_2E_f + \Delta_1 p_f c\right)^4 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i}} \times \ln\left[\left(\left[E_f + p_fc\right]\right.\right. \\ & \left.\left[4p_i^2 p_f^2 \sin^2\Theta_i\left(E_f - p_f c\right) + \left(\Delta_1 + \Delta_2\right)\left(\left[\Delta_2 E_f + \Delta_1 p_f c\right] - \sqrt{\left[\Delta_2 E_f + \Delta_1 p_f c\right]^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i}\right)\right]\right) \\ &\left[\left(E_f - p_f c\right)\left(4p_i^2 p_f^2 \sin^2\Theta_i\left[-E_f - p_f c\right]\right.\right. \\ & {} + \left.\left.\left(\Delta_1 - \Delta_2\right)\left(\left[\Delta_2 E_f + \Delta_1 p_f c\right] - \sqrt{\left(\Delta_2 E_f + \Delta_1 p_f c\right)^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i}\right]\right)\right]^{-1} \\ & {} \times \left[-\frac{ \left(\Delta_2^2 + 4p_i^2 p_f^2 \sin^2\Theta_i\right)\left(E_f^3 + E_f p_f^2 c^2\right) + p_f c\left(2\left[\Delta_1^2 - 4p_i^2 p_f^2 \sin^2\Theta_i\right]E_f p_f c + \Delta_1 \Delta_2\left[3E_f^2 + p_f^2 c^2\right]\right) } {\left(\Delta_2E_f + \Delta_1 p_f c\right)^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i} \right.\\ & {} -\frac{c\left(\Delta_2 E_f + \Delta_1 p_f c\right)}{p_f\left(E_i - cp_i \cos\Theta_i\right)} - \frac{ 4E_i^2 p_f^2 \left(2\left[\Delta_2 E_f + \Delta_1 p_f c\right]^2 - 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i\right)\left(\Delta_1 E_f + \Delta_2 p_f c\right) } {\left(\left[\Delta_2 E_f + \Delta_1 p_f c\right]^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i\right)^2} \\ & {} + \left.\frac{ 8p_i^2 p_f^2 m^2 c^4 \sin^2\Theta_i\left(E_i^2 + E_f^2\right) - 2\hbar^2\omega^2 p_i^2 \sin^2\Theta_i p_f c\left(\Delta_2 E_f + \Delta_1 p_f c\right) + 2\hbar^2 \omega^2 p_f m^2 c^3\left(\Delta_2 E_f + \Delta_1 p_f c\right) } {\left(E_i - cp_i\cos\Theta_i\right)\left(\left[\Delta_2 E_f + \Delta_1 p_f c\right]^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i\right)}\right], \\ I_4 ={} & {} -\frac {4\pi A p_f c\left(\Delta_2 E_f + \Delta_1 p_f c\right)} {\left(\Delta_2E_f + \Delta_1 p_f c\right)^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i} - \frac {16\pi E_i^2 p_f^2 A\left(\Delta_2E_f + \Delta_1 p_f c\right)^2} {\left(\left[\Delta_2 E_f + \Delta_1 p_f c\right]^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i\right)^2}, \\ I_5 ={} & \frac {4\pi A} { \left(-\Delta_2^2 + \Delta_1^2 - 4 p_i^2 p_f^2 \sin^2\Theta_i\right) \left(\left[\Delta_2 E_f + \Delta_1 p_f c\right]^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i\right) } \\ & {} \times\left[\frac{\hbar^2 \omega^2 p_f^2}{E_i - cp_i\cos\Theta_i}\right.\\ & {} \times\frac{ E_f\left(2\Delta_2^2\left[\Delta_2^2 - \Delta_1^2\right] + 8p_i^2 p_f^2 \sin^2\Theta_i\left[\Delta_2^2 + \Delta_1^2\right]\right) + p_f c\left(2\Delta_1\Delta_2\left[\Delta_2^2 - \Delta_1^2\right] + 16\Delta_1\Delta_2 p_i^2 p_f^2 \sin^2\Theta_i\right) } {\Delta_2^2 + 4p_i^2 p_f^2 \sin^2\Theta_i} \\ & {} + \frac {2\hbar^2 \omega^2 p_i^2 \sin^2\Theta_i \left(2\Delta_1\Delta_2 p_f c + 2\Delta_2^2 E_f + 8p_i^2 p_f^2 \sin^2\Theta_i E_f\right)} {E_i - cp_i\cos\Theta_i} \\ & {} + \frac {2E_i^2 p_f^2 \left( 2\left[\Delta_2^2 - \Delta_1^2\right]\left[\Delta_2 E_f + \Delta_1 p_f c\right]^2 + 8p_i^2 p_f^2 \sin^2\Theta_i\left[\left(\Delta_1^2 + \Delta_2^2\right)\left(E_f^2 + p_f^2 c^2\right) + 4\Delta_1\Delta_2 E_f p_f c\right] \right) } {\left(\Delta_2 E_f + \Delta_1 p_f c\right)^2 + 4m^2 c^4 p_i^2 p_f^2 \sin^2\Theta_i} \\ & {} + \left.\frac{8p_i^2 p_f^2 \sin^2\Theta_i\left(E_i^2 + E_f^2\right)\left(\Delta_2p_fc + \Delta_1 E_f\right)}{E_i - cp_i\cos\Theta_i}\right], \\ I_6 ={} & \frac{16\pi E_f^2 p_i^2 \sin^2\Theta_i A}{\left(E_i - cp_i\cos\Theta_i\right)^2 \left(-\Delta_2^2 + \Delta_1^2 - 4p_i^2 p_f^2 \sin^2\Theta_i\right)}, \end{align} }[/math]

and

[math]\displaystyle{ \begin{align} A &= \frac{Z^2\alpha_\text{fine}^3}{(2\pi)^2} \frac{\left|\mathbf{p}_f\right|}{\left|\mathbf{p}_i\right|} \frac{\hbar^2}{\omega} \\ \Delta_1 &= -\mathbf{p}_i^2 - \mathbf{p}_f^2 - \left(\frac{\hbar}{c}\omega\right)^2 + 2\frac{\hbar}{c} \omega\left|\mathbf{p}_i\right|\cos\Theta_i, \\ \Delta_2 &= -2\frac{\hbar}{c}\omega\left|\mathbf{p}_f\right| + 2\left|\mathbf{p}_i\right|\left|\mathbf{p}_f\right|\cos\Theta_i. \end{align} }[/math]

However, a much simpler expression for the same integral can be found in (Eq. 2BN) and in (Eq. 4.1).

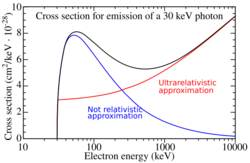
An analysis of the doubly differential cross section above shows that electrons whose kinetic energy is larger than the rest energy (511 keV) emit photons in forward direction while electrons with a small energy emit photons isotropically.

Electron–electron bremsstrahlung

One mechanism, considered important for small atomic numbers [math]\displaystyle{ Z }[/math], is the scattering of a free electron at the shell electrons of an atom or molecule. Since electron–electron bremsstrahlung is a function of [math]\displaystyle{ Z }[/math] and the usual electron-nucleus bremsstrahlung is a function of [math]\displaystyle{ Z^2 }[/math], electron–electron bremsstrahlung is negligible for metals. For air, however, it plays an important role in the production of terrestrial gamma-ray flashes.

See also

• Beamstrahlung
• Cyclotron radiation
• Wiggler (synchrotron)
• Free-electron laser
• History of X-rays
• Landau–Pomeranchuk–Migdal effect
• Nuclear fusion: bremsstrahlung losses
• Radiation length characterising energy loss by bremsstrahlung by high energy electrons in matter
• Synchrotron light source

Further reading

• Eberhard Haug; Werner Nakel (2004). The elementary process of bremsstrahlung. Scientific Lecture Notes in Physics. 73. River Edge, NJ: World Scientific. ISBN 978-981-238-578-9. https://books.google.com/books?id=v4FMtIwTri8C. 

External links

• Index of Early Bremsstrahlung Articles