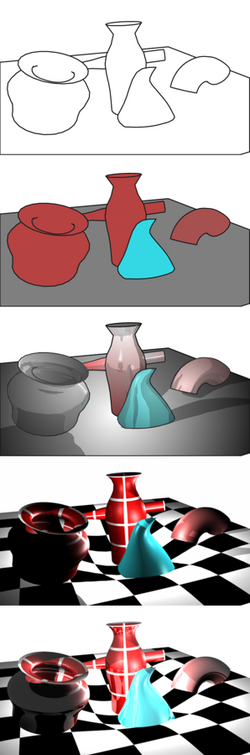
Rendering (computer graphics)

From HandWiki
Revision as of 22:18, 6 February 2024 by John Marlo (talk | contribs) (simplify)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Process of generating an image from a model
A variety of rendering techniques applied to a single 3D scene
An image created by using POV-Ray 3.6

Rendering or image synthesis is the process of generating a photorealistic or non-photorealistic image from a 2D or 3D model by means of a computer program.[citation needed] The resulting image is referred to as the render. Multiple models can be defined in a scene file containing objects in a strictly defined language or data structure. The scene file contains geometry, viewpoint, texture, lighting, and shading information describing the virtual scene. The data contained in the scene file is then passed to a rendering program to be processed and output to a digital image or raster graphics image file. The term "rendering" is analogous to the concept of an artist's impression of a scene. The term "rendering" is also used to describe the process of calculating effects in a video editing program to produce the final video output.

Rendering is one of the major sub-topics of 3D computer graphics, and in practice it is always connected to the others. It is the last major step in the graphics pipeline, giving models and animation their final appearance. With the increasing sophistication of computer graphics since the 1970s, it has become a more distinct subject.

Rendering has uses in architecture, video games, simulators, movie and TV visual effects, and design visualization, each employing a different balance of features and techniques. A wide variety of renderers are available for use. Some are integrated into larger modeling and animation packages, some are stand-alone, and some are free open-source projects. On the inside, a renderer is a carefully engineered program based on multiple disciplines, including light physics, visual perception, mathematics, and software development.

Though the technical details of rendering methods vary, the general challenges to overcome in producing a 2D image on a screen from a 3D representation stored in a scene file are handled by the graphics pipeline in a rendering device such as a GPU. A GPU is a purpose-built device that assists a CPU in performing complex rendering calculations. If a scene is to look relatively realistic and predictable under virtual lighting, the rendering software must solve the rendering equation. The rendering equation does not account for all lighting phenomena, but instead acts as a general lighting model for computer-generated imagery.

In the case of 3D graphics, scenes can be pre-rendered or generated in realtime. Pre-rendering is a slow, computationally intensive process that is typically used for movie creation, where scenes can be generated ahead of time, while real-time rendering is often done for 3D video games and other applications that must dynamically create scenes. 3D hardware accelerators can improve realtime rendering performance.

Usage

When the pre-image (a wireframe sketch usually) is complete, rendering is used, which adds in bitmap textures or procedural textures, lights, bump mapping and relative position to other objects. The result is a completed image the consumer or intended viewer sees.

For movie animations, several images (frames) must be rendered, and stitched together in a program capable of making an animation of this sort. Most 3D image editing programs can do this.

Features

A rendered image can be understood in terms of a number of visible features. Rendering research and development has been largely motivated by finding ways to simulate these efficiently. Some relate directly to particular algorithms and techniques, while others are produced together.

  • Shading – how the color and brightness of a surface varies with lighting
  • Texture-mapping – a method of applying detail to surfaces
  • Bump-mapping – a method of simulating small-scale bumpiness on surfaces
  • Fogging/participating medium – how light dims when passing through non-clear atmosphere or air
  • Shadows – the effect of obstructing light
  • Soft shadows – varying darkness caused by partially obscured light sources
  • Reflection – mirror-like or highly glossy reflection
  • Transparency (optics), transparency (graphic) or opacity – sharp transmission of light through solid objects
  • Translucency – highly scattered transmission of light through solid objects
  • Refraction – bending of light associated with transparency
  • Diffraction – bending, spreading, and interference of light passing by an object or aperture that disrupts the ray
  • Indirect illumination – surfaces illuminated by light reflected off other surfaces, rather than directly from a light source (also known as global illumination)
  • Caustics (a form of indirect illumination) – reflection of light off a shiny object, or focusing of light through a transparent object, to produce bright highlights on another object
  • Depth of field – objects appear blurry or out of focus when too far in front of or behind the object in focus
  • Motion blur – objects appear blurry due to high-speed motion, or the motion of the camera
  • Non-photorealistic rendering – rendering of scenes in an artistic style, intended to look like a painting or drawing

Techniques

Many rendering algorithms have been researched, and software used for rendering may employ a number of different techniques to obtain a final image.

Choosing how to render a scene usually involves a trade-off between speed and realism (although realism is not always desired). The techniques developed over the years follow a loose progression, with more advanced methods becoming practical as computing power and memory capacity increased.

An important distinction is between image order algorithms, which iterate over pixels of the image plane, and object order algorithms, which iterate over objects in the scene. For simple scenes, object order is usually more efficient, as there are fewer objects than pixels.

Rasterization (including scanline rendering)
Geometrically projects objects in the scene to an image plane. Different realistic or stylized effects can be obtained by coloring the pixels covered by the objects in different ways. Surfaces are typically divided into meshes of triangles before being rasterized. Rasterization is usually synonymous with "object order" rendering (as described above).
Ray casting
Uses geometric formulas to compute the first object that a ray intersects.[1]:8 It can be used to implement "image order" rendering by casting a ray for each pixel, and finding a corresponding point in the scene. Ray casting is a fundamental operation used for both graphical and non-graphical purposes,[1]:6 e.g. determining whether a point is in shadow, or checking what an enemy can see in a game.
Ray tracing
Simulates the bouncing paths of light caused by specular reflection and refraction, requiring a varying number of ray casting operations for each path. Advanced forms use Monte Carlo techniques to render effects such as area lights, depth of field, blurry reflections, and soft shadows, but computing global illumination is usually in the domain of path tracing.[1]:9-13[2]
Path tracing
Uses Monte Carlo integration with a simplified form of ray tracing, computing the average brightness of a sample of the possible paths that a photon could take when traveling from a light source to the camera (for some images, thousands of paths need to be sampled per pixel[1]:8). It was introduced as a statistically unbiased way to solve the rendering equation, giving ray tracing a rigorous mathematical foundation.[3][1]:11-13
Radiosity
A finite element analysis approach that breaks surfaces in the scene into pieces, and estimates the amount of light that each piece receives from light sources, or indirectly from other surfaces. Once the irradiance of each surface is known, the scene can be rendered using rasterization or ray tracing.[4]:888-890, 1044-1045

Each of the above approaches has many variations, and there is some overlap. Path tracing may be considered either a distinct technique or a particular type of ray tracing.[4]:846, 1021 Note that the usage of terminology related to ray tracing and path tracing has changed significantly over time.[1]:7

Rendering of a fractal terrain by ray marching

Ray marching is a family of algorithms, used by ray casting, for finding intersections between a ray and a complex object, such as a volumetric dataset or a surface defined by a signed distance function. It is not, by itself, a rendering method, but it can be incorporated into ray tracing and path tracing, and is used by rasterization to implement screen-space reflection and other effects.[1]:13

A technique called photon mapping or photon tracing uses forward ray tracing (also called particle tracing), tracing paths of photons from a light source to an object, rather than backward from the camera. The additional data collected by this process is used together with conventional backward ray tracing or path tracing.[4]:1037-1039 Rendering a scene using only forward ray tracing is impractical, even though it corresponds more closely to reality, because a huge number of photons would need to be simulated, only a tiny fraction of which actually hit the camera.[5]:7-9

Real-time rendering, including video game graphics, typically uses rasterization, but increasingly combines it with ray tracing and path tracing.[6]:2 To enable realistic global illumination, real-time rendering often relies on pre-rendered ("baked") lighting for stationary objects. For moving objects, it may use a technique called light probes, in which lighting is recorded by rendering omnidirectional views of the scene at chosen points in space (often points on a grid to allow easier interpolation). These are similar to environment maps, but typically use a very low resolution or an approximation such as spherical harmonics.[7] (Note: Blender uses the term 'light probes' for a more general class of pre-recorded lighting data, including reflection maps.[8])

Examples comparing different rendering techniques
  • 3D rendered image showing three copies of a cartoon cow. The one on the left has a mirror surface, and the one on the right uses a transparent glass material. The shadows of the cows are blocky (like blurry pixels) due to low quality settings in the renderer.

    A low quality rasterized image, rendered by Blender's EEVEE renderer with low shadow map resolution and a low-resolution mesh.

  • 3D rendered image showing three copies of a cartoon cow. The one on the left has a mirror surface, and the one on the right uses a transparent glass material. The image is speckled with many white dots, especially in the shadowed areas, due to low quality settings in the renderer. The reflection, transparency, and lighting are realistic, but the speckles distract from this.

    A low quality path traced image, rendered by Blender's Cycles renderer with only 16 sampled paths per pixel and a low-resolution mesh.

  • 3D rendered image showing three copies of a cartoon cow. The one on the left has a mirror surface, and the one on the right uses a transparent glass material. The outlines are angular and there are some defects (due to the low-resolution mesh of the models), and the transparent cow has no shadow.

    A ray traced image, using the POV-Ray program (using only its ray-tracing features) with a low-resolution mesh.

  • 3D rendered image showing three copies of a cartoon cow. The one on the left has a mirror surface, and the one on the right uses a transparent glass material. The outlines of the cows and the shadows are smooth with no blockiness or angular defects, and the reflection looks quite realistic, but the transparency does not look convincing, and the lighting in the shadowed areas of the cows is not quite realistic.

    A higher quality rasterized image, using Blender's EEVEE renderer with light probes.

  • 3D rendered image showing three copies of a cartoon cow. The one on the left has a mirror surface, and the one on the right uses a transparent glass material. The outlines of the cows and the shadows are smooth with no blockiness or angular defects. There are a few speckles of white pixels, but far fewer than in the low-quality image. The reflection, transparency, and lighting look realistic.

    A higher quality path traced image, using Blender's Cycles renderer with 2000 sampled paths per pixel.

  • 3D rendered image showing three copies of a cartoon cow. The one on the left has a mirror surface, and the one on the right uses a transparent glass material. The outlines of the cows and the shadows are smooth with no blockiness or angular defects. The lighting is realistic, including in the shadowed areas. The base surface is illuminated by bright spots and lines ("caustics") caused by light being focused by the reflective and transparent cows.

    An image rendered using POV-Ray's ray tracing, radiosity and photon mapping features.

  • 3D rendered image showing three copies of a cartoon cow. The one on the left has a metalic surface, and the one on the right uses a transparent glass material. The cow in the center appears made of glazed porcelain. The cows are standing on a wooden table. Lights and other background details from a cafe environment are reflected in the slightly glossy table and the cows.

    A more realistic path traced image, using Blender's Cycles renderer with image-based lighting.

Scanline rendering and rasterization

Rendering of the Extremely Large Telescope

A high-level representation of an image necessarily contains elements in a different domain from pixels. These elements are referred to as primitives. In a schematic drawing, for instance, line segments and curves might be primitives. In a graphical user interface, windows and buttons might be the primitives. In rendering of 3D models, triangles and polygons in space might be primitives.

If a pixel-by-pixel (image order) approach to rendering is impractical or too slow for some task, then a primitive-by-primitive (object order) approach to rendering may prove useful. Here, one loop through each of the primitives, determines which pixels in the image it affects, and modifies those pixels accordingly. This is called rasterization, and is the rendering method used by all current graphics cards.

Rasterization is frequently faster than pixel-by-pixel rendering. First, large areas of the image may be empty of primitives; rasterization will ignore these areas, but pixel-by-pixel rendering must pass through them. Second, rasterization can improve cache coherency and reduce redundant work by taking advantage of the fact that the pixels occupied by a single primitive tend to be contiguous in the image. For these reasons, rasterization is usually the approach of choice when interactive rendering is required; however, the pixel-by-pixel approach can often produce higher-quality images and is more versatile because it does not depend on as many assumptions about the image as rasterization.

The older form of rasterization is characterized by rendering an entire face (primitive) as a single color. Alternatively, rasterization can be done in a more complicated manner by first rendering the vertices of a face and then rendering the pixels of that face as a blending of the vertex colors. This version of rasterization has overtaken the old method as it allows the graphics to flow without complicated textures (a rasterized image when used face by face tends to have a very block-like effect if not covered in complex textures; the faces are not smooth because there is no gradual color change from one primitive to the next). This newer method of rasterization utilizes the graphics card's more taxing shading functions and still achieves better performance because the simpler textures stored in memory use less space. Sometimes designers will use one rasterization method on some faces and the other method on others based on the angle at which that face meets other joined faces, thus increasing speed and not hurting the overall effect.

Ray casting

Main page: Ray casting

In ray casting the geometry which has been modeled is parsed pixel by pixel, line by line, from the point of view outward, as if casting rays out from the point of view. Where an object is intersected, the color value at the point may be evaluated using several methods. In the simplest, the color value of the object at the point of intersection becomes the value of that pixel. The color may be determined from a texture-map. A more sophisticated method is to modify the color value by an illumination factor, but without calculating the relationship to a simulated light source. To reduce artifacts, a number of rays in slightly different directions may be averaged.

Ray casting involves calculating the "view direction" (from camera position), and incrementally following along that "ray cast" through "solid 3d objects" in the scene, while accumulating the resulting value from each point in 3D space. This is related and similar to "ray tracing" except that the raycast is usually not "bounced" off surfaces (where the "ray tracing" indicates that it is tracing out the lights path including bounces). "Ray casting" implies that the light ray is following a straight path (which may include traveling through semi-transparent objects). The ray cast is a vector that can originate from the camera or from the scene endpoint ("back to front", or "front to back"). Sometimes the final light value is derived from a "transfer function" and sometimes it's used directly.

Rough simulations of optical properties may be additionally employed: a simple calculation of the ray from the object to the point of view is made. Another calculation is made of the angle of incidence of light rays from the light source(s), and from these as well as the specified intensities of the light sources, the value of the pixel is calculated. Another simulation uses illumination plotted from a radiosity algorithm, or a combination of these two.

Ray tracing

Spiral Sphere and Julia, Detail, a computer-generated image created by visual artist Robert W. McGregor using only POV-Ray 3.6 and its built-in scene description language
Main page: Ray tracing (graphics)

Ray tracing aims to simulate the natural flow of light, interpreted as particles. Often, ray tracing methods are utilized to approximate the solution to the rendering equation by applying Monte Carlo methods to it. Some of the most used methods are path tracing, bidirectional path tracing, or Metropolis light transport, but also semi realistic methods are in use, like Whitted Style Ray Tracing, or hybrids. While most implementations let light propagate on straight lines, applications exist to simulate relativistic spacetime effects.[9]

In a final, production quality rendering of a ray traced work, multiple rays are generally shot for each pixel, and traced not just to the first object of intersection, but rather, through a number of sequential 'bounces', using the known laws of optics such as "angle of incidence equals angle of reflection" and more advanced laws that deal with refraction and surface roughness.

Once the ray either encounters a light source, or more probably once a set limiting number of bounces has been evaluated, then the surface illumination at that final point is evaluated using techniques described above, and the changes along the way through the various bounces evaluated to estimate a value observed at the point of view. This is all repeated for each sample, for each pixel.

In distribution ray tracing, at each point of intersection, multiple rays may be spawned. In path tracing, however, only a single ray or none is fired at each intersection, utilizing the statistical nature of Monte Carlo experiments.

As part of the approach known as physically based rendering, path tracing has become the dominant technique for rendering realistic scenes, including effects for movies.[10] For example, the popular open source 3D software Blender uses path tracing in its Cycles renderer.[11] Images produced using path tracing for global illumination are generally noisier than when using radiosity (the main competing algorithm), but radiosity can be difficult to apply to complex scenes and is prone to artifacts that arise from using a tessellated representation of irradiance.[10][4]:975-976, 1045

Path tracing's relative simplicity and its nature as a Monte Carlo method (sampling hundreds or thousands of paths per pixel) make it attractive to implement on a GPU, especially on recent GPUs that support ray tracing acceleration technology such as Nvidia's RTX and OptiX.[12] Many techniques have been developed to denoise the output of path tracing, reducing the number of paths required to achieve acceptable quality, at the risk of losing some detail or introducing small-scale artifacts that are more objectionable than noise;[13][14] neural networks are now widely used for this purpose.[15][16][17]

Advances in GPU technology have made real-time ray tracing possible in games, although it is currently almost always used in combination with rasterization.[6]:2 This enables visual effects that are difficult with only rasterization, including reflection from curved surfaces and interreflective objects,[18]:305 and shadows that are accurate over a wide range of distances and surface orientations.[1]:159-160 Ray tracing support is included in recent versions of the graphics APIs used by games, such as DirectX, Metal, and Vulkan.[19]

Neural rendering

Neural rendering is a rendering method using artificial neural networks.[20][21] Neural rendering includes image-based rendering methods that are used to reconstruct 3D models from 2-dimensional images.[20]One of these methods are photogrammetry, which is a method in which a collection of images from multiple angles of an object are turned into a 3D model. There have also been recent developments in generating and rendering 3D models from text and coarse paintings by notably Nvidia, Google and various other companies.


Radiosity

Main page: Radiosity (computer graphics)

Radiosity is a method which attempts to simulate the way in which directly illuminated surfaces act as indirect light sources that illuminate other surfaces. This produces more realistic shading and seems to better capture the 'ambience' of an indoor scene. A classic example is a way that shadows 'hug' the corners of rooms.

The optical basis of the simulation is that some diffused light from a given point on a given surface is reflected in a large spectrum of directions and illuminates the area around it.

The simulation technique may vary in complexity. Many renderings have a very rough estimate of radiosity, simply illuminating an entire scene very slightly with a factor known as ambiance. However, when advanced radiosity estimation is coupled with a high quality ray tracing algorithm, images may exhibit convincing realism, particularly for indoor scenes.

In advanced radiosity simulation, recursive, finite-element algorithms 'bounce' light back and forth between surfaces in the model, until some recursion limit is reached. The colouring of one surface in this way influences the colouring of a neighbouring surface, and vice versa. The resulting values of illumination throughout the model (sometimes including for empty spaces) are stored and used as additional inputs when performing calculations in a ray-casting or ray-tracing model.

Due to the iterative/recursive nature of the technique, complex objects are particularly slow to emulate. Prior to the standardization of rapid radiosity calculation, some digital artists used a technique referred to loosely as false radiosity by darkening areas of texture maps corresponding to corners, joints and recesses, and applying them via self-illumination or diffuse mapping for scanline rendering. Even now, advanced radiosity calculations may be reserved for calculating the ambiance of the room, from the light reflecting off walls, floor and ceiling, without examining the contribution that complex objects make to the radiosity – or complex objects may be replaced in the radiosity calculation with simpler objects of similar size and texture.

Radiosity calculations are viewpoint independent which increases the computations involved, but makes them useful for all viewpoints. If there is little rearrangement of radiosity objects in the scene, the same radiosity data may be reused for a number of frames, making radiosity an effective way to improve on the flatness of ray casting, without seriously impacting the overall rendering time-per-frame.

Because of this, radiosity is a prime component of leading real-time rendering methods, and has been used from beginning-to-end to create a large number of well-known recent feature-length animated 3D-cartoon films.

Sampling and filtering

One problem that any rendering system must deal with, no matter which approach it takes, is the sampling problem. Essentially, the rendering process tries to depict a continuous function from image space to colors by using a finite number of pixels. As a consequence of the Nyquist–Shannon sampling theorem (or Kotelnikov theorem), any spatial waveform that can be displayed must consist of at least two pixels, which is proportional to image resolution. In simpler terms, this expresses the idea that an image cannot display details, peaks or troughs in color or intensity, that are smaller than one pixel.

If a naive rendering algorithm is used without any filtering, high frequencies in the image function will cause ugly aliasing to be present in the final image. Aliasing typically manifests itself as jaggies, or jagged edges on objects where the pixel grid is visible. In order to remove aliasing, all rendering algorithms (if they are to produce good-looking images) must use some kind of low-pass filter on the image function to remove high frequencies, a process called antialiasing.

Optimization

Due to the large number of calculations, a work in progress is usually only rendered in detail appropriate to the portion of the work being developed at a given time, so in the initial stages of modeling, wireframe and ray casting may be used, even where the target output is ray tracing with radiosity. It is also common to render only parts of the scene at high detail, and to remove objects that are not important to what is currently being developed.

For real-time, it is appropriate to simplify one or more common approximations, and tune to the exact parameters of the scenery in question, which is also tuned to the agreed parameters to get the most 'bang for the buck'.

Academic core

Main page: Unbiased rendering

The implementation of a realistic renderer always has some basic element of physical simulation or emulation – some computation which resembles or abstracts a real physical process.

The term "physically based" indicates the use of physical models and approximations that are more general and widely accepted outside rendering. A particular set of related techniques have gradually become established in the rendering community.

The basic concepts are moderately straightforward, but intractable to calculate; and a single elegant algorithm or approach has been elusive for more general purpose renderers. In order to meet demands of robustness, accuracy and practicality, an implementation will be a complex combination of different techniques.

Rendering research is concerned with both the adaptation of scientific models and their efficient application.

The rendering equation

Main page: Rendering equation

This is the key academic/theoretical concept in rendering. It serves as the most abstract formal expression of the non-perceptual aspect of rendering. All more complete algorithms can be seen as solutions to particular formulations of this equation.

[math]\displaystyle{ L_o(x, \omega) = L_e(x, \omega) + \int_\Omega L_i(x, \omega') f_r(x, \omega', \omega) (\omega' \cdot n) \, \mathrm d \omega' }[/math]

Meaning: at a particular position and direction, the outgoing light (Lo) is the sum of the emitted light (Le) and the reflected light. The reflected light being the sum of the incoming light (Li) from all directions, multiplied by the surface reflection and incoming angle. By connecting outward light to inward light, via an interaction point, this equation stands for the whole 'light transport' – all the movement of light – in a scene.

The bidirectional reflectance distribution function

The bidirectional reflectance distribution function (BRDF) expresses a simple model of light interaction with a surface as follows:

[math]\displaystyle{ f_r(x, \omega', \omega) = \frac{\mathrm d L_r(x, \omega)}{L_i(x, \omega')(\omega' \cdot \vec n) \mathrm d \omega'} }[/math]

Light interaction is often approximated by the even simpler models: diffuse reflection and specular reflection, although both can ALSO be BRDFs.

Geometric optics

Rendering is practically exclusively concerned with the particle aspect of light physics – known as geometrical optics. Treating light, at its basic level, as particles bouncing around is a simplification, but appropriate: the wave aspects of light are negligible in most scenes, and are significantly more difficult to simulate. Notable wave aspect phenomena include diffraction (as seen in the colours of CDs and DVDs) and polarisation (as seen in LCDs). Both types of effect, if needed, are made by appearance-oriented adjustment of the reflection model.

Visual perception

Though it receives less attention, an understanding of human visual perception is valuable to rendering. This is mainly because image displays and human perception have restricted ranges. A renderer can simulate a wide range of light brightness and color, but current displays – movie screen, computer monitor, etc. – cannot handle so much, and something must be discarded or compressed. Human perception also has limits, and so does not need to be given large-range images to create realism. This can help solve the problem of fitting images into displays, and, furthermore, suggest what short-cuts could be used in the rendering simulation, since certain subtleties will not be noticeable. This related subject is tone mapping.

Mathematics used in rendering includes: linear algebra, calculus, numerical mathematics, signal processing, and Monte Carlo methods.

Rendering for movies often takes place on a network of tightly connected computers known as a render farm.

The current[when?] state of the art in 3-D image description for movie creation is the Mental Ray scene description language designed at Mental Images and RenderMan Shading Language designed at Pixar[22] (compare with simpler 3D fileformats such as VRML or APIs such as OpenGL and DirectX tailored for 3D hardware accelerators).

Other renderers (including proprietary ones) can and are sometimes used, but most other renderers tend to miss one or more of the often needed features like good texture filtering, texture caching, programmable shaders, highend geometry types like hair, subdivision or nurbs surfaces with tesselation on demand, geometry caching, raytracing with geometry caching, high quality shadow mapping, speed or patent-free implementations. Other highly sought features these days may include interactive photorealistic rendering (IPR) and hardware rendering/shading.

Chronology of important published ideas

Rendering of an ESTCube-1 satellite



See also


References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Cite error: Invalid <ref> tag; no text was provided for refs named {{{1}}}
  2. ↑ Cook, Robert L. (April 11, 2019). "5. Stochastic Sampling and Distributed Ray Tracing". in Glassner, Andrew S.. An Introduction to Ray Tracing. ACADEMIC PRESS. ISBN 0-12-286160-4. https://www.realtimerendering.com/raytracing/An-Introduction-to-Ray-Tracing-The-Morgan-Kaufmann-Series-in-Computer-Graphics-.pdf. 
  3. ↑ Kajiya, James T. (August 1986). "The Rendering Equation". SIGGRAPH Comput. Graph. 20 (4): 143–150. doi:10.1145/15886.15902. https://doi.org/10.1145/15886.15902. Retrieved 27 January 2024. 
  4. ↑ 4.0 4.1 4.2 4.3 Glassner, Andrew S. (2011). Principles of digital image synthesis. Morgan Kaufmann Publishers, Inc.. ISBN 1-55860-276-3. https://www.realtimerendering.com/Principles_of_Digital_Image_Synthesis_v1.0.1.pdf. 
  5. ↑ Glassner, Andrew S. (April 11, 2019). "1. An Overview of Ray Tracing". An Introduction to Ray Tracing. ACADEMIC PRESS. ISBN 0-12-286160-4. https://www.realtimerendering.com/raytracing/An-Introduction-to-Ray-Tracing-The-Morgan-Kaufmann-Series-in-Computer-Graphics-.pdf. 
  6. ↑ 6.0 6.1 Akenine-Möller, Tomas; Haines, Eric; Hoffman, Naty; Pesce, Angelo; Iwanicki, Michał; Hillaire, Sébastien (August 6, 2018). "Online chapter 26. Real-Time Ray Tracing". Real-Time Rendering (4th ed.). Boca Raton, FL: A K Peters/CRC Press. ISBN 978-1138627000. 
  7. ↑ "Unity Manual:Light Probes: Introduction". https://docs.unity3d.com/540/Documentation/Manual/LightProbes.html. 
  8. ↑ "Blender Manual: Rendering: EEVEE: Light Probes: Introduction". The Blender Foundation. https://docs.blender.org/manual/en/latest/render/eevee/light_probes/introduction.html. 
  9. ↑ Relativistic Ray-Tracing: Simulating the Visual Appearance of Rapidly Moving Objects. 1995. 
  10. ↑ 10.0 10.1 Pharr, Matt; Jakob, Wenzel; Humphreys, Greg (March 28, 2023). Physically Based Rendering: From Theory to Implementation (4th ed.). Cambridge, Massachusetts: The MIT Press. ISBN 978-0262048026. https://pbr-book.org/4ed/contents. 
  11. ↑ "Blender Manual: Rendering: Cycles: Introduction". The Blender Foundation. https://docs.blender.org/manual/en/4.0/render/cycles/introduction.html. 
  12. ↑ Pharr, Matt; Jakob, Wenzel; Humphreys, Greg (March 28, 2023). "15. Wavefront Rendering on GPUs". Physically Based Rendering: From Theory to Implementation (4th ed.). Cambridge, Massachusetts: The MIT Press. ISBN 978-0262048026. https://pbr-book.org/4ed/contents. 
  13. ↑ Pharr, Matt; Jakob, Wenzel; Humphreys, Greg (March 28, 2023). Physically Based Rendering: From Theory to Implementation (4th ed.). Cambridge, Massachusetts: The MIT Press. ISBN 978-0262048026. https://pbr-book.org/4ed/contents. 
  14. ↑ "Blender Manual: Rendering: Cycles: Optimizing Renders: Reducing Noise". The Blender Foundation. https://docs.blender.org/manual/en/4.0/render/cycles/optimizations/reducing_noise.html. 
  15. ↑ "Blender Manual: Rendering: Cycles: Render Settings: Sampling". The Blender Foundation. https://docs.blender.org/manual/en/4.0/render/cycles/render_settings/sampling.html#render-cycles-settings-viewport-denoising. 
  16. ↑ "Intel® Open Image Denoise: High-Performance Denoising Library for Ray Tracing". Intel Corporation. https://www.openimagedenoise.org/. 
  17. ↑ "NVIDIA OptiX™ AI-Accelerated Denoiser". NVIDIA Corporation. https://developer.nvidia.com/optix-denoiser. 
  18. ↑ Liu, Edward; Llamas, Ignacio; Cañada, Juan; Kelly, Patrick (February 25, 2019). "19: Cinematic Rendering in UE4 with Real-Time Ray Tracing and Denoising". Ray Tracing Gems: High-Quality and Real-Time Rendering with DXR and Other APIs. Berkeley, CA: Apress. ISBN 978-1-4842-4427-2. https://link.springer.com/book/10.1007/978-1-4842-4427-2. 
  19. ↑ "Khronos Blog: Ray Tracing In Vulkan". The Khronos® Group Inc. December 15, 2020. https://www.khronos.org/blog/ray-tracing-in-vulkan. 
  20. ↑ 20.0 20.1 Tewari, A.; Fried, O.; Thies, J.; Sitzmann, V.; Lombardi, S.; Sunkavalli, K.; Martin-Brualla, R.; Simon, T. et al. (2020). "State of the Art on Neural Rendering". Computer Graphics Forum 39 (2): 701–727. doi:10.1111/cgf.14022. https://onlinelibrary.wiley.com/doi/am-pdf/10.1111/cgf.14022. 
  21. ↑ Knight, Will. "A New Trick Lets Artificial Intelligence See in 3D" (in en-US). Wired. ISSN 1059-1028. https://www.wired.com/story/new-way-ai-see-3d/. Retrieved 2022-02-08. 
  22. ↑ Raghavachary, Saty (30 July 2006). "A brief introduction to RenderMan". ACM SIGGRAPH 2006 Courses on - SIGGRAPH '06. ACM. pp. 2. doi:10.1145/1185657.1185817. ISBN 978-1595933645. http://dl.acm.org/citation.cfm?id=1185657.1185817. Retrieved 7 May 2018. 
  23. ↑ Appel, A. (1968). "Some techniques for shading machine renderings of solids". 32. pp. 37–49. http://graphics.stanford.edu/courses/Appel.pdf. 
  24. ↑ Bouknight, W. J. (1970). "A procedure for generation of three-dimensional half-tone computer graphics presentations". Communications of the ACM 13 (9): 527–536. doi:10.1145/362736.362739. 
  25. ↑ Gouraud, H. (1971). "Continuous shading of curved surfaces". IEEE Transactions on Computers 20 (6): 623–629. doi:10.1109/t-c.1971.223313. http://www.cs.uiowa.edu/~cwyman/classes/spring05-22C251/papers/ContinuousShadingOfCurvedSurfaces.pdf. 
  26. ↑ 26.0 26.1 26.2 26.3 "History | School of Computing" (in en-US). https://www.cs.utah.edu/about/history/. 
  27. ↑ Phong, B-T (1975). "Illumination for computer generated pictures". Communications of the ACM 18 (6): 311–316. doi:10.1145/360825.360839. http://jesper.kalliope.org/blog/library/p311-phong.pdf. 
  28. ↑ Bui Tuong Phong, Illumination for computer generated pictures , Communications of ACM 18 (1975), no. 6, 311–317.
  29. ↑ 29.0 29.1 Putas. "The way to home 3d". http://vintage3d.org/history.php. 
  30. ↑ 30.0 30.1 Catmull, E. (1974). A subdivision algorithm for computer display of curved surfaces (PDF) (PhD thesis). University of Utah. Archived from the original (PDF) on 2014-11-14. Retrieved 2011-07-15.
  31. ↑ Blinn, J.F.; Newell, M.E. (1976). "Texture and reflection in computer generated images". Communications of the ACM 19 (10): 542–546. doi:10.1145/360349.360353. 
  32. ↑ Blinn, James F. (20 July 1977). "Models of light reflection for computer synthesized pictures". ACM SIGGRAPH Computer Graphics 11 (2): 192–198. doi:10.1145/965141.563893. 
  33. ↑ "Bomber - Videogame by Sega". http://www.arcade-museum.com/game_detail.php?game_id=12797. 
  34. ↑ Crow, F.C. (1977). "Shadow algorithms for computer graphics". 11. pp. 242–248. http://design.osu.edu/carlson/history/PDFs/crow-shadows.pdf. Retrieved 2011-07-15. 
  35. ↑ Williams, L. (1978). "Casting curved shadows on curved surfaces". 12. pp. 270–274. 
  36. ↑ Blinn, J.F. (1978). "Simulation of wrinkled surfaces". Computer Graphics (Proceedings of SIGGRAPH 1978). 12. pp. 286–292. http://research.microsoft.com/pubs/73939/p286-blinn.pdf. 
  37. ↑ Wolf, Mark J. P. (15 June 2012). Before the Crash: Early Video Game History. Wayne State University Press. ISBN 978-0814337226. https://books.google.com/books?id=oK3D4i5ldKgC&pg=PA173. Retrieved 7 May 2018. 
  38. ↑ Fuchs, H.; Kedem, Z.M.; Naylor, B.F. (1980). "On visible surface generation by a priori tree structures". Computer Graphics (Proceedings of SIGGRAPH 1980). 14. pp. 124–133. 
  39. ↑ Whitted, T. (1980). "An improved illumination model for shaded display". Communications of the ACM 23 (6): 343–349. doi:10.1145/358876.358882. 
  40. ↑ Purcaru, Bogdan Ion (13 March 2014). "Games vs. Hardware. The History of PC video games: The 80's". Purcaru Ion Bogdan. https://books.google.com/books?id=lB4PAwAAQBAJ&pg=PA181. 
  41. ↑ "System 16 - Sega VCO Object Hardware (Sega)". http://www.system16.com/hardware.php?id=690. 
  42. ↑ Cook, R.L.; Torrance, K.E. (1981). "A reflectance model for computer graphics". Computer Graphics (Proceedings of SIGGRAPH 1981). 15. pp. 307–316. 
  43. ↑ Williams, L. (1983). "Pyramidal parametrics". Computer Graphics (Proceedings of SIGGRAPH 1983). 17. pp. 1–11. 
  44. ↑ Glassner, A.S. (1984). "Space subdivision for fast ray tracing". IEEE Computer Graphics & Applications 4 (10): 15–22. doi:10.1109/mcg.1984.6429331. 
  45. ↑ Porter, T.; Duff, T. (1984). "Compositing digital images". Computer Graphics (Proceedings of SIGGRAPH 1984). 18. pp. 253–259. http://keithp.com/~keithp/porterduff/p253-porter.pdf. 
  46. ↑ Cook, R.L.; Porter, T.; Carpenter, L. (1984). "Distributed ray tracing". Computer Graphics (Proceedings of SIGGRAPH 1984). 18. pp. 137–145. http://www.cs.rutgers.edu/~nealen/teaching/cs428_fall09/readings/cook84.pdf. [yes|permanent dead link|dead link}}]
  47. ↑ Goral, C.; Torrance, K.E.; Greenberg, D.P.; Battaile, B. (1984). "Modeling the interaction of light between diffuse surfaces". Computer Graphics (Proceedings of SIGGRAPH 1984). 18. pp. 213–222. 
  48. ↑ "Archived copy". http://cgfm2.emuviews.com/txt/s16tech.txt. 
  49. ↑ Cohen, M.F.; Greenberg, D.P. (1985). "The hemi-cube: a radiosity solution for complex environments". Computer Graphics (Proceedings of SIGGRAPH 1985). 19. pp. 31–40. doi:10.1145/325165.325171. http://www.arnetminer.org/dev.do?m=downloadpdf&url=http://arnetminer.org/pdf/PDFFiles2/--g---g-Index1255026826706/The%20hemi-cube%20%20a%20radiosity%20solution%20for%20complex%20environments1255058011060.pdf. Retrieved 2020-03-25. 
  50. ↑ Arvo, J. (1986). "Backward ray tracing". SIGGRAPH 1986 Developments in Ray Tracing course notes. 
  51. ↑ Kajiya, J. (1986). "The rendering equation". Computer Graphics (Proceedings of SIGGRAPH 1986). 20. pp. 143–150. 
  52. ↑ Cook, R.L.; Carpenter, L.; Catmull, E. (1987). "The Reyes image rendering architecture". Computer Graphics (Proceedings of SIGGRAPH 1987). 21. pp. 95–102. http://graphics.pixar.com/library/Reyes/paper.pdf. 
  53. ↑ 53.0 53.1 53.2 "MAME | SRC/Mame/Drivers/Namcos21.c". http://mamedev.org/source/src/mame/drivers/namcos21.c.html. 
  54. ↑ Wu, Xiaolin (July 1991). An efficient antialiasing technique. 25. 143–152. doi:10.1145/127719.122734. ISBN 978-0-89791-436-9. http://portal.acm.org/citation.cfm?id=122734. 
  55. ↑ Wu, Xiaolin (1991). "Fast Anti-Aliased Circle Generation". in James Arvo. Graphics Gems II. San Francisco: Morgan Kaufmann. pp. 446–450. ISBN 978-0-12-064480-3. 
  56. ↑ Hanrahan, P.; Salzman, D.; Aupperle, L. (1991). "A rapid hierarchical radiosity algorithm". Computer Graphics (Proceedings of SIGGRAPH 1991). 25. pp. 197–206. 
  57. ↑ "IGN Presents the History of SEGA". 21 April 2009. http://ign.com/articles/2009/04/21/ign-presents-the-history-of-sega?page=8. 
  58. ↑ "System 16 - Sega Model 2 Hardware (Sega)". http://www.system16.com/hardware.php?id=713. 
  59. ↑ 59.0 59.1 59.2 59.3 "System 16 - Namco Magic Edge Hornet Simulator Hardware (Namco)". http://www.system16.com/hardware.php?id=832. 
  60. ↑ M. Oren and S.K. Nayar, "Generalization of Lambert's Reflectance Model ". SIGGRAPH. pp.239-246, Jul, 1994
  61. ↑ Tumblin, J.; Rushmeier, H.E. (1993). "Tone reproduction for realistic computer generated images". IEEE Computer Graphics & Applications 13 (6): 42–48. doi:10.1109/38.252554. http://smartech.gatech.edu/bitstream/handle/1853/3686/92-31.pdf?sequence=1. 
  62. ↑ Hanrahan, P.; Krueger, W. (1993). "Reflection from layered surfaces due to subsurface scattering". Computer Graphics (Proceedings of SIGGRAPH 1993). 27. pp. 165–174. 
  63. ↑ Miller, Gavin (24 July 1994). "Efficient algorithms for local and global accessibility shading". Proceedings of the 21st annual conference on Computer graphics and interactive techniques - SIGGRAPH '94. ACM. pp. 319–326. doi:10.1145/192161.192244. ISBN 978-0897916677. http://dl.acm.org/citation.cfm?id=192161.192244. Retrieved 7 May 2018. 
  64. ↑ "Archived copy". http://www.hotchips.org/wp-content/uploads/hc_archives/hc07/3_Tue/HC7.S5/HC7.5.1.pdf. 
  65. ↑ Jensen, H.W.; Christensen, N.J. (1995). "Photon maps in bidirectional monte carlo ray tracing of complex objects". Computers & Graphics 19 (2): 215–224. doi:10.1016/0097-8493(94)00145-o. 
  66. ↑ "System 16 - Sega Model 3 Step 1.0 Hardware (Sega)". http://www.system16.com/hardware.php?id=717. 
  67. ↑ Veach, E.; Guibas, L. (1997). "Metropolis light transport". Computer Graphics (Proceedings of SIGGRAPH 1997). 16. pp. 65–76. 
  68. ↑ Keller, A. (1997). "Instant Radiosity". Computer Graphics (Proceedings of SIGGRAPH 1997). 24. pp. 49–56. 
  69. ↑ "Hardware Review: Neon 250 Specs & Features". http://www3.sharkyextreme.com/hardware/reviews/video/neon250/2.shtml. 
  70. ↑ Lewis, J. P.; Cordner, Matt; Fong, Nickson (1 July 2000). "Pose space deformation: A unified approach to shape interpolation and skeleton-driven deformation". Proceedings of the 27th annual conference on Computer graphics and interactive techniques - SIGGRAPH '00. ACM Press/Addison-Wesley Publishing Co.. pp. 165–172. doi:10.1145/344779.344862. ISBN 978-1581132083. 
  71. ↑ Sloan, P.; Kautz, J.; Snyder, J. (2002). "Precomputed Radiance Transfer for Real-Time Rendering in Dynamic, Low Frequency Lighting Environments". Computer Graphics (Proceedings of SIGGRAPH 2002). 29. pp. 527–536. http://www.mpi-inf.mpg.de/~jnkautz/projects/prt/prtSIG02.pdf. 

Cite error: <ref> tag with name "RayTracingGems_1" defined in <references> is not used in prior text.

Cite error: <ref> tag with name "RayTracingGems_13" defined in <references> is not used in prior text.

Further reading


External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Rendering_(computer_graphics)&oldid=3384255"