Modular group

Short description: Orientation-preserving mapping class group of the torus

In mathematics, the modular group is the projective special linear group [math]\displaystyle{ \operatorname{PSL}(2,\mathbb Z) }[/math] of 2 × 2 matrices with integer coefficients and determinant 1. The matrices $A$ and $- A$ are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic.

Definition

The modular group $Γ$ is the group of linear fractional transformations of the upper half of the complex plane, which have the form

[math]\displaystyle{ z\mapsto\frac{az+b}{cz+d} }[/math]

where $a$ , $b$ , $c$ , $d$ are integers, and $ad - bc = 1$ . The group operation is function composition.

This group of transformations is isomorphic to the projective special linear group $PSL(2, Z)$ , which is the quotient of the 2-dimensional special linear group $SL(2, Z)$ over the integers by its center ${I, - I}$ . In other words, $PSL(2, Z)$ consists of all matrices

[math]\displaystyle{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} }[/math]

where $a$ , $b$ , $c$ , $d$ are integers, $ad - bc = 1$ , and pairs of matrices $A$ and $- A$ are considered to be identical. The group operation is the usual multiplication of matrices.

Some authors define the modular group to be $PSL(2, Z)$ , and still others define the modular group to be the larger group $SL(2, Z)$ .

Some mathematical relations require the consideration of the group $GL(2, Z)$ of matrices with determinant plus or minus one. ( $SL(2, Z)$ is a subgroup of this group.) Similarly, $PGL(2, Z)$ is the quotient group $GL(2, Z)/{I, - I}$ . A 2 × 2 matrix with unit determinant is a symplectic matrix, and thus $SL(2, Z) = Sp(2, Z)$ , the symplectic group of 2 × 2 matrices.

Finding elements

To find an explicit matrix

[math]\displaystyle{ \begin{pmatrix} a & x \\ b & y \end{pmatrix} }[/math]

in $SL(2, Z)$ , begin with two coprime integers [math]\displaystyle{ a,b }[/math], and solve the determinant equation

[math]\displaystyle{ ay-bx = 1. }[/math]

(Notice the determinant equation forces [math]\displaystyle{ a,b }[/math] to be coprime since otherwise there would be a factor [math]\displaystyle{ c\gt 1 }[/math] such that [math]\displaystyle{ ca' = a }[/math], [math]\displaystyle{ cb' = b }[/math], hence

[math]\displaystyle{ c(a'y-b'x) = 1 }[/math]

would have no integer solutions.) For example, if [math]\displaystyle{ a = 7, \text{ } b =6 }[/math] then the determinant equation reads

[math]\displaystyle{ 7y-6x = 1 }[/math]

then taking [math]\displaystyle{ y = -5 }[/math] and [math]\displaystyle{ x = -6 }[/math] gives [math]\displaystyle{ -35 - (-36) = 1 }[/math], hence

[math]\displaystyle{ \begin{pmatrix} 7 & -6 \\ 6 & -5 \end{pmatrix} }[/math]

is a matrix. Then, using the projection, these matrices define elements in $PSL(2, Z)$ .

Number-theoretic properties

The unit determinant of

[math]\displaystyle{ \begin{pmatrix} a & b \\ c & d \end{pmatrix} }[/math]

implies that the fractions _{$a / b$}, _{$a / c$}, _{$c / d$}, _{$b / d$} are all irreducible, that is having no common factors (provided the denominators are non-zero, of course). More generally, if $p / q$ is an irreducible fraction, then

[math]\displaystyle{ \frac{ap+bq}{cp+dq} }[/math]

is also irreducible (again, provided the denominator be non-zero). Any pair of irreducible fractions can be connected in this way; that is, for any pair $p / q$ and $r / s$ of irreducible fractions, there exist elements

[math]\displaystyle{ \begin{pmatrix} a & b \\ c & d \end{pmatrix}\in\operatorname{SL}(2, \mathbb Z) }[/math]

such that

[math]\displaystyle{ r = ap+bq \quad \mbox{ and } \quad s=cp+dq. }[/math]

Elements of the modular group provide a symmetry on the two-dimensional lattice. Let $ω 1$ and $ω 2$ be two complex numbers whose ratio is not real. Then the set of points

[math]\displaystyle{ \Lambda (\omega_1, \omega_2)=\{ m\omega_1 +n\omega_2 : m,n\in \mathbb Z \} }[/math]

is a lattice of parallelograms on the plane. A different pair of vectors $α 1$ and $α 2$ will generate exactly the same lattice if and only if

[math]\displaystyle{ \begin{pmatrix}\alpha_1 \\ \alpha_2 \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} \omega_1 \\ \omega_2 \end{pmatrix} }[/math]

for some matrix in $GL(2, Z)$ . It is for this reason that doubly periodic functions, such as elliptic functions, possess a modular group symmetry.

The action of the modular group on the rational numbers can most easily be understood by envisioning a square grid, with grid point $(p, q)$ corresponding to the fraction $p / q$ (see Euclid's orchard). An irreducible fraction is one that is visible from the origin; the action of the modular group on a fraction never takes a visible (irreducible) to a hidden (reducible) one, and vice versa.

Note that any member of the modular group maps the projectively extended real line one-to-one to itself, and furthermore bijectively maps the projectively extended rational line (the rationals with infinity) to itself, the irrationals to the irrationals, the transcendental numbers to the transcendental numbers, the non-real numbers to the non-real numbers, the upper half-plane to the upper half-plane, et cetera.

If $p n -1 / q n -1$ and $p n / q n$ are two successive convergents of a continued fraction, then the matrix

[math]\displaystyle{ \begin{pmatrix} p_{n-1} & p_{n} \\ q_{n-1} & q_{n} \end{pmatrix} }[/math]

belongs to $GL(2, Z)$ . In particular, if $bc - ad = 1$ for positive integers $a$ , $b$ , $c$ , $d$ with $a < b$ and $c < d$ then $a / b$ and $c / d$ will be neighbours in the Farey sequence of order $max(b, d)$ . Important special cases of continued fraction convergents include the Fibonacci numbers and solutions to Pell's equation. In both cases, the numbers can be arranged to form a semigroup subset of the modular group.

Group-theoretic properties

Presentation

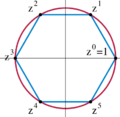
The modular group can be shown to be generated by the two transformations

[math]\displaystyle{ \begin{align} S &: z\mapsto -\frac1z \\ T &: z\mapsto z+1 \end{align} }[/math]

so that every element in the modular group can be represented (in a non-unique way) by the composition of powers of $S$ and $T$ . Geometrically, $S$ represents inversion in the unit circle followed by reflection with respect to the imaginary axis, while $T$ represents a unit translation to the right.

The generators $S$ and $T$ obey the relations $S 2 = 1$ and $(ST) 3 = 1$ . It can be shown ^[1] that these are a complete set of relations, so the modular group has the presentation:

[math]\displaystyle{ \Gamma \cong \left\langle S, T \mid S^2=I, \left(ST\right)^3=I \right\rangle }[/math]

This presentation describes the modular group as the rotational triangle group $D(2, 3, \infty)$ (infinity as there is no relation on $T$ ), and it thus maps onto all triangle groups $(2, 3, n)$ by adding the relation $T n = 1$ , which occurs for instance in the congruence subgroup $Γ(n)$ .

Using the generators $S$ and $ST$ instead of $S$ and $T$ , this shows that the modular group is isomorphic to the free product of the cyclic groups $C 2$ and $C 3$ :

[math]\displaystyle{ \Gamma \cong C_2 * C_3 }[/math]

The action of $T : z \mapsto z + 1$ on $H$
The action of $S : z \mapsto - 1 / z$ on $H$

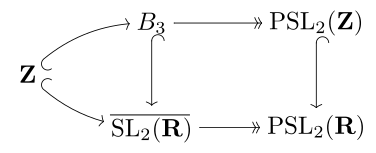
Braid group

The braid group

B 3

is the universal central extension of the modular group.

The braid group $B 3$ is the universal central extension of the modular group, with these sitting as lattices inside the (topological) universal covering group $SL 2 (R) \to PSL 2 (R)$ . Further, the modular group has a trivial center, and thus the modular group is isomorphic to the quotient group of $B 3$ modulo its center; equivalently, to the group of inner automorphisms of $B 3$ .

The braid group $B 3$ in turn is isomorphic to the knot group of the trefoil knot.

Quotients

The quotients by congruence subgroups are of significant interest.

Other important quotients are the $(2, 3, n)$ triangle groups, which correspond geometrically to descending to a cylinder, quotienting the $x$ coordinate modulo $n$ , as $T n = (z \mapsto z + n)$ . $(2, 3, 5)$ is the group of icosahedral symmetry, and the $(2, 3, 7)$ triangle group (and associated tiling) is the cover for all Hurwitz surfaces.

Presenting as a matrix group

The group [math]\displaystyle{ \text{SL}_2(\mathbb{Z}) }[/math] can be generated by the two matrices^[2]

[math]\displaystyle{ S = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}, \text{ } T = \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} }[/math]

since

[math]\displaystyle{ S^2 = -I_2, \text{ } (ST)^3 = \begin{pmatrix} 0 & -1 \\ 1 & 1 \end{pmatrix}^3 = -I_2 }[/math]

The projection [math]\displaystyle{ \text{SL}_2(\mathbb{Z}) \to \text{PSL}_2(\mathbb{Z}) }[/math] turns these matrices into generators of [math]\displaystyle{ \text{PSL}_2(\mathbb{Z}) }[/math], with relations similar to the group presentation.

Relationship to hyperbolic geometry

See also: PSL2(R)

The modular group is important because it forms a subgroup of the group of isometries of the hyperbolic plane. If we consider the upper half-plane model $H$ of hyperbolic plane geometry, then the group of all orientation-preserving isometries of $H$ consists of all Möbius transformations of the form

[math]\displaystyle{ z\mapsto \frac{az + b}{cz + d} }[/math]

where $a$ , $b$ , $c$ , $d$ are real numbers. In terms of projective coordinates, the group $PSL(2, R)$ acts on the upper half-plane $H$ by projectivity:

[math]\displaystyle{ [z,\ 1]\begin{pmatrix} a & c \\ b & d \end{pmatrix} \,= \, [az + b,\ cz +d] \,\thicksim\, \left[\frac{az + b}{cz + d}, \ 1\right]. }[/math]

This action is faithful. Since $PSL(2, Z)$ is a subgroup of $PSL(2, R)$ , the modular group is a subgroup of the group of orientation-preserving isometries of $H$ .^[3]

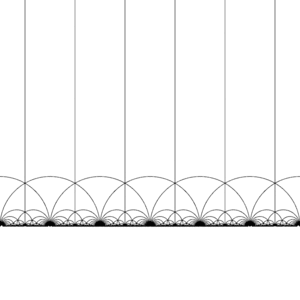
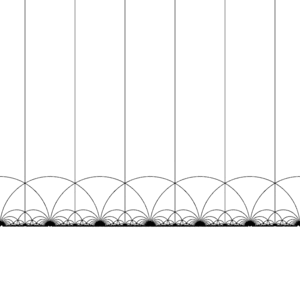
Tessellation of the hyperbolic plane

A typical fundamental domain for the action of

Γ

on the upper half-plane.

The modular group $Γ$ acts on [math]\displaystyle{ \mathbb H }[/math] as a discrete subgroup of [math]\displaystyle{ \operatorname{PSL}(2,\mathbb R) }[/math], that is, for each $z$ in [math]\displaystyle{ \mathbb H }[/math] we can find a neighbourhood of $z$ which does not contain any other element of the orbit of $z$ . This also means that we can construct fundamental domains, which (roughly) contain exactly one representative from the orbit of every $z$ in $H$ . (Care is needed on the boundary of the domain.)

There are many ways of constructing a fundamental domain, but a common choice is the region

[math]\displaystyle{ R = \left\{ z \in \mathbb H \colon \left| z \right| \gt 1,\, \left| \operatorname{Re}(z) \right| \lt \tfrac12 \right\} }[/math]

bounded by the vertical lines $Re(z) = 1 / 2$ and $Re(z) = - 1 / 2$ , and the circle $| z | = 1$ . This region is a hyperbolic triangle. It has vertices at $1 / 2 + i \sqrt 3 / 2$ and $- 1 / 2 + i \sqrt 3 / 2$ , where the angle between its sides is $π / 3$ , and a third vertex at infinity, where the angle between its sides is 0.

There is a strong connection between the modular group and elliptic curves. Each point [math]\displaystyle{ z }[/math] in the upper half-plane gives an elliptic curve, namely the quotient of [math]\displaystyle{ \mathbb{C} }[/math] by the lattice generated by 1 and [math]\displaystyle{ z }[/math]. Two points in the upper half-plane give isomorphic elliptic curves if and only if they are related by a transformation in the modular group. Thus, the quotient of the upper half-plane by the action of the modular group is the so-called moduli space of elliptic curves: a space whose points describe isomorphism classes of elliptic curves. This is often visualized as the fundamental domain described above, with some points on its boundary identified.

The modular group and its subgroups are also a source of interesting tilings of the hyperbolic plane. By transforming this fundamental domain in turn by each of the elements of the modular group, a regular tessellation of the hyperbolic plane by congruent hyperbolic triangles known as the V6.6.∞ Infinite-order triangular tiling is created. Note that each such triangle has one vertex either at infinity or on the real axis $Im(z) = 0$ .

This tiling can be extended to the Poincaré disk, where every hyperbolic triangle has one vertex on the boundary of the disk. The tiling of the Poincaré disk is given in a natural way by the $J$ -invariant, which is invariant under the modular group, and attains every complex number once in each triangle of these regions.

This tessellation can be refined slightly, dividing each region into two halves (conventionally colored black and white), by adding an orientation-reversing map; the colors then correspond to orientation of the domain. Adding in $(x, y) \mapsto (- x, y)$ and taking the right half of the region $R$ (where $Re(z) \geq 0$ ) yields the usual tessellation. This tessellation first appears in print in (Klein 1878/79a),^[4] where it is credited to Richard Dedekind, in reference to (Dedekind 1877).^[4]^[5]

Visualization of the map

(2, 3, \infty) \to (2, 3, 7)

by morphing the associated tilings.^[6]

The map of groups $(2, 3, \infty) \to (2, 3, n)$ (from modular group to triangle group) can be visualized in terms of this tiling (yielding a tiling on the modular curve), as depicted in the video at right.

Congruence subgroups

Main page: Congruence subgroup

Important subgroups of the modular group $Γ$ , called congruence subgroups, are given by imposing congruence relations on the associated matrices.

There is a natural homomorphism $SL(2, Z) \to SL(2, Z / N Z)$ given by reducing the entries modulo $N$ . This induces a homomorphism on the modular group $PSL(2, Z) \to PSL(2, Z / N Z)$ . The kernel of this homomorphism is called the principal congruence subgroup of level $N$ , denoted $Γ(N)$ . We have the following short exact sequence:

[math]\displaystyle{ 1\to\Gamma(N)\to\Gamma\to\operatorname{PSL}(2, \mathbb Z/N\mathbb Z) \to 1. }[/math]

Being the kernel of a homomorphism $Γ(N)$ is a normal subgroup of the modular group $Γ$ . The group $Γ(N)$ is given as the set of all modular transformations

[math]\displaystyle{ z\mapsto\frac{az+b}{cz+d} }[/math]

for which $a \equiv d \equiv \pm1 (mod N)$ and $b \equiv c \equiv 0 (mod N)$ .

It is easy to show that the trace of a matrix representing an element of $Γ(N)$ cannot be −1, 0, or 1, so these subgroups are torsion-free groups. (There are other torsion-free subgroups.)

The principal congruence subgroup of level 2, $Γ(2)$ , is also called the modular group $Λ$ . Since $PSL(2, Z /2 Z)$ is isomorphic to $S 3$ , $Λ$ is a subgroup of index 6. The group $Λ$ consists of all modular transformations for which $a$ and $d$ are odd and $b$ and $c$ are even.

Another important family of congruence subgroups are the modular group $Γ 0 (N)$ defined as the set of all modular transformations for which $c \equiv 0 (mod N)$ , or equivalently, as the subgroup whose matrices become upper triangular upon reduction modulo $N$ . Note that $Γ(N)$ is a subgroup of $Γ 0 (N)$ . The modular curves associated with these groups are an aspect of monstrous moonshine – for a prime number $p$ , the modular curve of the normalizer is genus zero if and only if $p$ divides the order of the monster group, or equivalently, if $p$ is a supersingular prime.

Dyadic monoid

One important subset of the modular group is the dyadic monoid, which is the monoid of all strings of the form $ST k ST m ST n ...$ for positive integers $k, m, n,...$ . This monoid occurs naturally in the study of fractal curves, and describes the self-similarity symmetries of the Cantor function, Minkowski's question mark function, and the Koch snowflake, each being a special case of the general de Rham curve. The monoid also has higher-dimensional linear representations; for example, the $N = 3$ representation can be understood to describe the self-symmetry of the blancmange curve.

Maps of the torus

The group $GL(2, Z)$ is the linear maps preserving the standard lattice $Z 2$ , and $SL(2, Z)$ is the orientation-preserving maps preserving this lattice; they thus descend to self-homeomorphisms of the torus (SL mapping to orientation-preserving maps), and in fact map isomorphically to the (extended) mapping class group of the torus, meaning that every self-homeomorphism of the torus is isotopic to a map of this form. The algebraic properties of a matrix as an element of $GL(2, Z)$ correspond to the dynamics of the induced map of the torus.

Hecke groups

The modular group can be generalized to the Hecke groups, named for Erich Hecke, and defined as follows.^[7]

The Hecke group $H q$ with $q \geq 3$ , is the discrete group generated by

[math]\displaystyle{ \begin{align} z &\mapsto -\frac1z \\ z &\mapsto z + \lambda_q, \end{align} }[/math]

where $λ q = 2 cos π / q$ . For small values of $q \geq 3$ , one has:

[math]\displaystyle{ \begin{align} \lambda_3 &= 1, \\ \lambda_4 &= \sqrt{2}, \\ \lambda_5 &= \frac{1+\sqrt{5}}{2}, \\ \lambda_6 &= \sqrt{3}, \\ \lambda_8 &= \sqrt{2+\sqrt{2}}. \end{align} }[/math]

The modular group $Γ$ is isomorphic to $H 3$ and they share properties and applications – for example, just as one has the free product of cyclic groups

[math]\displaystyle{ \Gamma \cong C_2 * C_3, }[/math]

more generally one has

[math]\displaystyle{ H_q \cong C_2 * C_q, }[/math]

which corresponds to the triangle group $(2, q, \infty)$ . There is similarly a notion of principal congruence subgroups associated to principal ideals in $Z [λ]$ .

History

The modular group and its subgroups were first studied in detail by Richard Dedekind and by Felix Klein as part of his Erlangen programme in the 1870s. However, the closely related elliptic functions were studied by Joseph Louis Lagrange in 1785, and further results on elliptic functions were published by Carl Gustav Jakob Jacobi and Niels Henrik Abel in 1827.

References

↑ Alperin, Roger C. (April 1993). " $PSL 2 (Z) = Z 2 * Z 3$ ". Amer. Math. Monthly 100 (4): 385–386. doi:10.2307/2324963.
↑ Conrad, Keith. "SL(2,Z)". https://kconrad.math.uconn.edu/blurbs/grouptheory/SL(2,Z).pdf.
↑ McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian. "The Modular Group". The Mathematica Journal 9 (3). https://www.mathematica-journal.com/issue/v9i3/contents/ModularGroup/ModularGroup.pdf.
↑ ^4.0 ^4.1 Le Bruyn, Lieven (22 April 2008), Dedekind or Klein?, http://www.neverendingbooks.org/dedekind-or-klein
↑ Stillwell, John (January 2001). "Modular Miracles". The American Mathematical Monthly 108 (1): 70–76. doi:10.2307/2695682. ISSN 0002-9890.
↑ Westendorp, Gerard. "Platonic tessellations of Riemann surfaces". http://www.xs4all.nl/~westy31/Geometry/Geometry.html#Modular.
↑ Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis (2006). Combinatorial Group Theory, Discrete Groups, and Number Theory. p. 65. ISBN 9780821839850. https://books.google.com/books?id=5Unmxs7yeHwC&pg=PA65.

Apostol, Tom M. (1990). Modular Functions and Dirichlet Series in Number Theory (2nd ed.). New York: Springer. ch. 2. ISBN 0-387-97127-0.
Klein, Felix (1878–1879), "Über die Transformation der elliptischen Funktionen und die Auflösung der Gleichungen fünften Grades (On the transformation of elliptic functions and ...)", Math. Annalen 14: 13–75, doi:10.1007/BF02297507, http://mathdoc.emath.fr/cgi-bin/oetoc?id=OE_KLEIN__3, retrieved 3 June 2010
Dedekind, Richard (September 1877), "Schreiben an Herrn Borchardt über die Theorie der elliptische Modul-Functionen", Crelle's Journal 83: 265–292 .

0.00

(0 votes)

Original source: https://en.wikipedia.org/wiki/Modular group. Read more

[1] Alperin, Roger C. (April 1993). " $PSL 2 (Z) = Z 2 * Z 3$ ". Amer. Math. Monthly 100 (4): 385–386. doi:10.2307/2324963.

[2] Conrad, Keith. "SL(2,Z)". https://kconrad.math.uconn.edu/blurbs/grouptheory/SL(2,Z).pdf.

[3] McCreary, Paul R.; Murphy, Teri Jo; Carter, Christian. "The Modular Group". The Mathematica Journal 9 (3). https://www.mathematica-journal.com/issue/v9i3/contents/ModularGroup/ModularGroup.pdf.

[lebruyn-4] 4.0 ^4.1 Le Bruyn, Lieven (22 April 2008), Dedekind or Klein?, http://www.neverendingbooks.org/dedekind-or-klein

[5] Stillwell, John (January 2001). "Modular Miracles". The American Mathematical Monthly 108 (1): 70–76. doi:10.2307/2695682. ISSN 0002-9890.

[westendorp-6] Westendorp, Gerard. "Platonic tessellations of Riemann surfaces". http://www.xs4all.nl/~westy31/Geometry/Geometry.html#Modular.

[7] Rosenberger, Gerhard; Fine, Benjamin; Gaglione, Anthony M.; Spellman, Dennis (2006). Combinatorial Group Theory, Discrete Groups, and Number Theory. p. 65. ISBN 9780821839850. https://books.google.com/books?id=5Unmxs7yeHwC&pg=PA65.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Anonymous

Search

Modular group

Namespaces

More

Page actions

Contents