Infinite-order triangular tiling
From HandWiki
Short description: Concept in geometry
| Infinite-order triangular tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
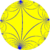
| Vertex configuration | 3∞ |
| Schläfli symbol | {3,∞} |
| Wythoff symbol | ∞ | 3 2 |
| Coxeter diagram |       
|
| Symmetry group | [∞,3], (*∞32) |
| Dual | Order-3 apeirogonal tiling |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
In geometry, the infinite-order triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,∞}. All vertices are ideal, located at "infinity" and seen on the boundary of the Poincaré hyperbolic disk projection.
Symmetry
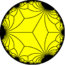
A lower symmetry form has alternating colors, and represented by cyclic symbol {(3,∞,3)}, 
. The tiling also represents the fundamental domains of the *∞∞∞ symmetry, which can be seen with 3 colors of lines representing 3 mirrors of the construction.
| 150px Alternated colored tiling |
150px *∞∞∞ symmetry |
150px Apollonian gasket with *∞∞∞ symmetry |
Related polyhedra and tiling
This tiling is topologically related as part of a sequence of regular polyhedra with Schläfli symbol {3,p}.
| *n32 symmetry mutation of regular tilings: {3,n} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclid. | Compact hyper. | Paraco. | Noncompact hyperbolic | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
| 3.3 | 33 | 34 | 35 | 36 | 37 | 38 | 3∞ | 312i | 39i | 36i | 33i |
| Paracompact uniform tilings in [∞,3] family | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [∞,3], (*∞32) | [∞,3]+ (∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
 = 
|
=
|
=
|
|
= or 
|
= or
|
= 
| ||||
|
|
|
|
|
|
|
|
|
| |
| {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | h2{∞,3} | s{3,∞} |
| Uniform duals | ||||||||||
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
||
| V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
| Paracompact hyperbolic uniform tilings in [(∞,3,3)] family | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(∞,3,3)], (*∞33) | [(∞,3,3)]+, (∞33) | ||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
| (∞,∞,3) | t0,1(∞,3,3) | t1(∞,3,3) | t1,2(∞,3,3) | t2(∞,3,3) | t0,2(∞,3,3) | t0,1,2(∞,3,3) | s(∞,3,3) | ||||
| Dual tilings | |||||||||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
||||||||||
| V(3.∞)3 | V3.∞.3.∞ | V(3.∞)3 | V3.6.∞.6 | V(3.3)∞ | V3.6.∞.6 | V6.6.∞ | V3.3.3.3.3.∞ | ||||
Other infinite-order triangular tilings
A nonregular infinite-order triangular tiling can be generated by a recursive process from a central triangle as shown here:
- 240px
See also
- Infinite-order tetrahedral honeycomb
- List of regular polytopes
- List of uniform planar tilings
- Tilings of regular polygons
- Triangular tiling
- Uniform tilings in hyperbolic plane
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8.
External links
- Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html.
- Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html.
 |  |
