Bernoulli's principle

Short description: Principle relating to fluid dynamics

A flow of air through a venturi meter. The kinetic energy increases at the expense of the fluid pressure, as shown by the difference in height of the two columns of water.

File:Venturi Tube en.webm

Bernoulli's principle is a key concept in fluid dynamics that relates pressure, speed and height. Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or the fluid's potential energy. The principle is named after the Swiss mathematician and physicist Daniel Bernoulli, who published it in his book Hydrodynamica in 1738. Although Bernoulli deduced that pressure decreases when the flow speed increases, it was Leonhard Euler in 1752 who derived Bernoulli's equation in its usual form.

Bernoulli's principle can be derived from the principle of conservation of energy. This states that, in a steady flow, the sum of all forms of energy in a fluid is the same at all points that are free of viscous forces. This requires that the sum of kinetic energy, potential energy and internal energy remains constant. Thus an increase in the speed of the fluid—implying an increase in its kinetic energy—occurs with a simultaneous decrease in (the sum of) its potential energy (including the static pressure) and internal energy. If the fluid is flowing out of a reservoir, the sum of all forms of energy is the same because in a reservoir the energy per unit volume (the sum of pressure and gravitational potential ρ g h) is the same everywhere.

Bernoulli's principle can also be derived directly from Isaac Newton's second Law of Motion. If a small volume of fluid is flowing horizontally from a region of high pressure to a region of low pressure, then there is more pressure behind than in front. This gives a net force on the volume, accelerating it along the streamline.

Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.

Bernoulli's principle is only applicable for isentropic flows: when the effects of irreversible processes (like turbulence) and non-adiabatic processes (e.g. thermal radiation) are small and can be neglected. However, the principle can be applied to various types of flow within these bounds, resulting in various forms of Bernoulli's equation. The simple form of Bernoulli's equation is valid for incompressible flows (e.g. most liquid flows and gases moving at low Mach number). More advanced forms may be applied to compressible flows at higher Mach numbers.

Incompressible flow equation

In most flows of liquids, and of gases at low Mach number, the density of a fluid parcel can be considered to be constant, regardless of pressure variations in the flow. Therefore, the fluid can be considered to be incompressible, and these flows are called incompressible flows. Bernoulli performed his experiments on liquids, so his equation in its original form is valid only for incompressible flow.

A common form of Bernoulli's equation is:

[math]\displaystyle{ \frac{v^2}{2} + gz + \frac{p}{\rho} = \text{constant} }[/math]

(A)

where:

• [math]\displaystyle{ v }[/math] is the fluid flow speed at a point,
• [math]\displaystyle{ g }[/math] is the acceleration due to gravity,
• [math]\displaystyle{ z }[/math] is the elevation of the point above a reference plane, with the positive [math]\displaystyle{ z }[/math]-direction pointing upward—so in the direction opposite to the gravitational acceleration,
• [math]\displaystyle{ p }[/math] is the pressure at the chosen point, and
• [math]\displaystyle{ \rho }[/math] is the density of the fluid at all points in the fluid.

Bernoulli's equation and the Bernoulli constant are applicable throughout any region of flow where the energy per unit mass is uniform. Because the energy per unit mass of liquid in a well-mixed reservoir is uniform throughout, Bernoulli's equation can be used to analyze the fluid flow everywhere in that reservoir (including pipes or flow fields that the reservoir feeds) except where viscous forces dominate and erode the energy per unit mass.

The following assumptions must be met for this Bernoulli equation to apply:

• the flow must be steady, that is, the flow parameters (velocity, density, etc.) at any point cannot change with time,
• the flow must be incompressible—even though pressure varies, the density must remain constant along a streamline;
• friction by viscous forces must be negligible.

For conservative force fields (not limited to the gravitational field), Bernoulli's equation can be generalized as: [math]\displaystyle{ \frac{v^2}{2} + \Psi + \frac{p}{\rho} = \text{constant} }[/math] where Ψ is the force potential at the point considered. For example, for the Earth's gravity Ψ = gz.

By multiplying with the fluid density ρ, equation (A) can be rewritten as: [math]\displaystyle{ \tfrac{1}{2} \rho v^2 + \rho g z + p = \text{constant} }[/math] or: [math]\displaystyle{ q + \rho g h = p_0 + \rho g z = \text{constant} }[/math] where

• q = 1/2ρv² is dynamic pressure,
• h = z + p/ρg is the piezometric head or hydraulic head (the sum of the elevation z and the pressure head) and
• p₀ = p + q is the stagnation pressure (the sum of the static pressure p and dynamic pressure q).

The constant in the Bernoulli equation can be normalized. A common approach is in terms of total head or energy head H: [math]\displaystyle{ H = z + \frac{p}{\rho g} + \frac{v^2}{2g} = h + \frac{v^2}{2g}, }[/math]

The above equations suggest there is a flow speed at which pressure is zero, and at even higher speeds the pressure is negative. Most often, gases and liquids are not capable of negative absolute pressure, or even zero pressure, so clearly Bernoulli's equation ceases to be valid before zero pressure is reached. In liquids—when the pressure becomes too low—cavitation occurs. The above equations use a linear relationship between flow speed squared and pressure. At higher flow speeds in gases, or for sound waves in liquid, the changes in mass density become significant so that the assumption of constant density is invalid.

Simplified form

In many applications of Bernoulli's equation, the change in the ρgz term is so small compared with the other terms that it can be ignored. For example, in the case of aircraft in flight, the change in height z is so small the ρgz term can be omitted. This allows the above equation to be presented in the following simplified form: [math]\displaystyle{ p + q = p_0 }[/math] where p₀ is called total pressure, and q is dynamic pressure. Many authors refer to the pressure p as static pressure to distinguish it from total pressure p₀ and dynamic pressure q. In Aerodynamics, L.J. Clancy writes: "To distinguish it from the total and dynamic pressures, the actual pressure of the fluid, which is associated not with its motion but with its state, is often referred to as the static pressure, but where the term pressure alone is used it refers to this static pressure."

The simplified form of Bernoulli's equation can be summarized in the following memorable word equation:

static pressure + dynamic pressure = total pressure

Every point in a steadily flowing fluid, regardless of the fluid speed at that point, has its own unique static pressure p and dynamic pressure q. Their sum p + q is defined to be the total pressure p₀. The significance of Bernoulli's principle can now be summarized as "total pressure is constant in any region free of viscous forces". If the fluid flow is brought to rest at some point, this point is called a stagnation point, and at this point the static pressure is equal to the stagnation pressure.

If the fluid flow is irrotational, the total pressure is uniform and Bernoulli's principle can be summarized as "total pressure is constant everywhere in the fluid flow". It is reasonable to assume that irrotational flow exists in any situation where a large body of fluid is flowing past a solid body. Examples are aircraft in flight and ships moving in open bodies of water. However, Bernoulli's principle importantly does not apply in the boundary layer such as in flow through long pipes.

Unsteady potential flow

The Bernoulli equation for unsteady potential flow is used in the theory of ocean surface waves and acoustics. For an irrotational flow, the flow velocity can be described as the gradient ∇φ of a velocity potential φ. In that case, and for a constant density ρ, the momentum equations of the Euler equations can be integrated to:[math]\displaystyle{ \frac{\partial \varphi}{\partial t} + \tfrac12 v^2 + \frac{p}{\rho} + gz = f(t), }[/math]

which is a Bernoulli equation valid also for unsteady—or time dependent—flows. Here ∂φ/∂t denotes the partial derivative of the velocity potential φ with respect to time t, and v = |∇φ| is the flow speed. The function f(t) depends only on time and not on position in the fluid. As a result, the Bernoulli equation at some moment t applies in the whole fluid domain. This is also true for the special case of a steady irrotational flow, in which case f and ∂φ/∂t are constants so equation (A) can be applied in every point of the fluid domain. Further f(t) can be made equal to zero by incorporating it into the velocity potential using the transformation:[math]\displaystyle{ \Phi = \varphi - \int_{t_0}^t f(\tau)\, \mathrm{d}\tau, }[/math] resulting in: [math]\displaystyle{ \frac{\partial \Phi}{\partial t} + \tfrac12 v^2 + \frac{p}{\rho} + gz = 0. }[/math]

Note that the relation of the potential to the flow velocity is unaffected by this transformation: ∇Φ = ∇φ.

The Bernoulli equation for unsteady potential flow also appears to play a central role in Luke's variational principle, a variational description of free-surface flows using the Lagrangian mechanics.

Compressible flow equation

Bernoulli developed his principle from observations on liquids, and Bernoulli's equation is valid for ideal fluids: those that are incompressible, irrotational, inviscid, and subjected to conservative forces. It is sometimes valid for the flow of gases: provided that there is no transfer of kinetic or potential energy from the gas flow to the compression or expansion of the gas. If both the gas pressure and volume change simultaneously, then work will be done on or by the gas. In this case, Bernoulli's equation—in its incompressible flow form—cannot be assumed to be valid. However, if the gas process is entirely isobaric, or isochoric, then no work is done on or by the gas (so the simple energy balance is not upset). According to the gas law, an isobaric or isochoric process is ordinarily the only way to ensure constant density in a gas. Also the gas density will be proportional to the ratio of pressure and absolute temperature; however, this ratio will vary upon compression or expansion, no matter what non-zero quantity of heat is added or removed. The only exception is if the net heat transfer is zero, as in a complete thermodynamic cycle or in an individual isentropic (frictionless adiabatic) process, and even then this reversible process must be reversed, to restore the gas to the original pressure and specific volume, and thus density. Only then is the original, unmodified Bernoulli equation applicable. In this case the equation can be used if the flow speed of the gas is sufficiently below the speed of sound, such that the variation in density of the gas (due to this effect) along each streamline can be ignored. Adiabatic flow at less than Mach 0.3 is generally considered to be slow enough.

It is possible to use the fundamental principles of physics to develop similar equations applicable to compressible fluids. There are numerous equations, each tailored for a particular application, but all are analogous to Bernoulli's equation and all rely on nothing more than the fundamental principles of physics such as Newton's laws of motion or the first law of thermodynamics.

Compressible flow in fluid dynamics

For a compressible fluid, with a barotropic equation of state, and under the action of conservative forces, [math]\displaystyle{ \frac {v^2}{2}+ \int_{p_1}^p \frac {\mathrm{d}\tilde{p}}{\rho\left(\tilde{p}\right)} + \Psi = \text{constant (along a streamline)} }[/math] where:

• p is the pressure
• ρ is the density and ρ(p) indicates that it is a function of pressure
• v is the flow speed
• Ψ is the potential associated with the conservative force field, often the gravitational potential

In engineering situations, elevations are generally small compared to the size of the Earth, and the time scales of fluid flow are small enough to consider the equation of state as adiabatic. In this case, the above equation for an ideal gas becomes: [math]\displaystyle{ \frac {v^2}{2}+ gz + \left(\frac {\gamma}{\gamma-1}\right) \frac {p}{\rho} = \text{constant (along a streamline)} }[/math] where, in addition to the terms listed above:

• γ is the ratio of the specific heats of the fluid
• g is the acceleration due to gravity
• z is the elevation of the point above a reference plane

In many applications of compressible flow, changes in elevation are negligible compared to the other terms, so the term gz can be omitted. A very useful form of the equation is then: [math]\displaystyle{ \frac {v^2}{2}+\left( \frac {\gamma}{\gamma-1}\right)\frac {p}{\rho} = \left(\frac {\gamma}{\gamma-1}\right)\frac {p_0}{\rho_0} }[/math]

where:

• p₀ is the total pressure
• ρ₀ is the total density

Compressible flow in thermodynamics

The most general form of the equation, suitable for use in thermodynamics in case of (quasi) steady flow, is:

[math]\displaystyle{ \frac{v^2}{2} + \Psi + w = \text{constant}. }[/math]

Here w is the enthalpy per unit mass (also known as specific enthalpy), which is also often written as h (not to be confused with "head" or "height").

Note that [math]\displaystyle{ w =e + \frac{p}{\rho} ~~~\left(= \frac{\gamma}{\gamma-1} \frac{p}{\rho}\right) }[/math] where e is the thermodynamic energy per unit mass, also known as the specific internal energy. So, for constant internal energy [math]\displaystyle{ e }[/math] the equation reduces to the incompressible-flow form.

The constant on the right-hand side is often called the Bernoulli constant and denoted b. For steady inviscid adiabatic flow with no additional sources or sinks of energy, b is constant along any given streamline. More generally, when b may vary along streamlines, it still proves a useful parameter, related to the "head" of the fluid (see below).

When the change in Ψ can be ignored, a very useful form of this equation is: [math]\displaystyle{ \frac{v^2}{2} + w = w_0 }[/math] where w₀ is total enthalpy. For a calorically perfect gas such as an ideal gas, the enthalpy is directly proportional to the temperature, and this leads to the concept of the total (or stagnation) temperature.

When shock waves are present, in a reference frame in which the shock is stationary and the flow is steady, many of the parameters in the Bernoulli equation suffer abrupt changes in passing through the shock. The Bernoulli parameter remains unaffected. An exception to this rule is radiative shocks, which violate the assumptions leading to the Bernoulli equation, namely the lack of additional sinks or sources of energy.

Unsteady potential flow

For a compressible fluid, with a barotropic equation of state, the unsteady momentum conservation equation [math]\displaystyle{ \frac{\partial \vec{v}}{\partial t} + \left(\vec{v}\cdot \nabla\right)\vec{v} = -\vec{g} - \frac{\nabla p}{\rho} }[/math]

With the irrotational assumption, namely, the flow velocity can be described as the gradient ∇φ of a velocity potential φ. The unsteady momentum conservation equation becomes [math]\displaystyle{ \frac{\partial \nabla \phi}{\partial t} + \nabla \left(\frac{\nabla \phi \cdot \nabla \phi}{2}\right) = -\nabla \Psi - \nabla \int_{p_1}^{p}\frac{d \tilde{p}}{\rho(\tilde{p})} }[/math] which leads to [math]\displaystyle{ \frac{\partial \phi}{\partial t} + \frac{\nabla \phi \cdot \nabla \phi}{2} + \Psi + \int_{p_1}^{p}\frac{d \tilde{p}}{\rho(\tilde{p})} = \text{constant} }[/math]

In this case, the above equation for isentropic flow becomes: [math]\displaystyle{ \frac{\partial \phi}{\partial t} + \frac{\nabla \phi \cdot \nabla \phi}{2} + \Psi + \frac{\gamma}{\gamma-1}\frac{p}{\rho} = \text{constant} }[/math]

Derivations

Bernoulli equation for incompressible fluids

The Bernoulli equation for incompressible fluids can be derived by either integrating Newton's second law of motion or by applying the law of conservation of energy, ignoring viscosity, compressibility, and thermal effects.

Derivation through integrating Newton's Second Law of Motion

The simplest derivation is to first ignore gravity and consider constrictions and expansions in pipes that are otherwise straight, as seen in Venturi effect. Let the x axis be directed down the axis of the pipe.

Define a parcel of fluid moving through a pipe with cross-sectional area A, the length of the parcel is dx, and the volume of the parcel A dx. If mass density is ρ, the mass of the parcel is density multiplied by its volume m = ρA dx. The change in pressure over distance dx is dp and flow velocity v = dx/dt.

Apply Newton's second law of motion (force = mass × acceleration) and recognizing that the effective force on the parcel of fluid is −A dp. If the pressure decreases along the length of the pipe, dp is negative but the force resulting in flow is positive along the x axis.

[math]\displaystyle{ \begin{align} m \frac{\mathrm{d}v}{\mathrm{d}t}&= F \\ \rho A \mathrm{d}x \frac{\mathrm{d}v}{\mathrm{d}t} &= -A \mathrm{d}p \\ \rho \frac{\mathrm{d}v}{\mathrm{d}t} &= -\frac{\mathrm{d}p}{\mathrm{d}x} \end{align} }[/math]

In steady flow the velocity field is constant with respect to time, v = v(x) = v(x(t)), so v itself is not directly a function of time t. It is only when the parcel moves through x that the cross sectional area changes: v depends on t only through the cross-sectional position x(t). [math]\displaystyle{ \frac{\mathrm{d}v}{\mathrm{d}t} = \frac{\mathrm{d}v}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}t} = \frac{\mathrm{d}v}{\mathrm{d}x}v = \frac{\mathrm{d}}{\mathrm{d}x} \left( \frac{v^2}{2} \right). }[/math]

With density ρ constant, the equation of motion can be written as [math]\displaystyle{ \frac{\mathrm{d}}{\mathrm{d}x} \left( \rho \frac{v^2}{2} + p \right) =0 }[/math] by integrating with respect to x [math]\displaystyle{ \frac{v^2}{2} + \frac{p}{\rho}= C }[/math] where C is a constant, sometimes referred to as the Bernoulli constant. It is not a universal constant, but rather a constant of a particular fluid system. The deduction is: where the speed is large, pressure is low and vice versa.

In the above derivation, no external work–energy principle is invoked. Rather, Bernoulli's principle was derived by a simple manipulation of Newton's second law.

A streamtube of fluid moving to the right. Indicated are pressure, elevation, flow speed, distance (s), and cross-sectional area. Note that in this figure elevation is denoted as h, contrary to the text where it is given by z.

Derivation by using conservation of energy

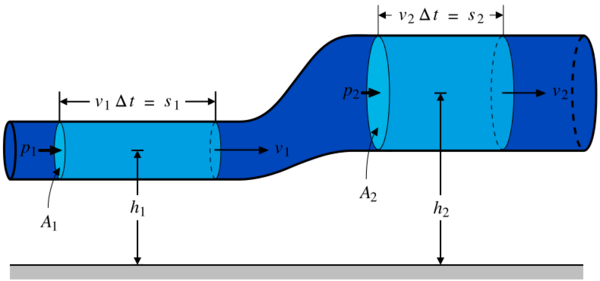
Another way to derive Bernoulli's principle for an incompressible flow is by applying conservation of energy. In the form of the work-energy theorem, stating that

the change in the kinetic energy E_kin of the system equals the net work W done on the system; [math]\displaystyle{ W = \Delta E_\text{kin}. }[/math]

Therefore,

the work done by the forces in the fluid equals increase in kinetic energy.

The system consists of the volume of fluid, initially between the cross-sections A₁ and A₂. In the time interval Δt fluid elements initially at the inflow cross-section A₁ move over a distance s₁ = v₁ Δt, while at the outflow cross-section the fluid moves away from cross-section A₂ over a distance s₂ = v₂ Δt. The displaced fluid volumes at the inflow and outflow are respectively A₁s₁ and A₂s₂. The associated displaced fluid masses are – when ρ is the fluid's mass density – equal to density times volume, so ρA₁s₁ and ρA₂s₂. By mass conservation, these two masses displaced in the time interval Δt have to be equal, and this displaced mass is denoted by Δm: [math]\displaystyle{ \begin{align} \rho A_1 s_1 &= \rho A_1 v_1 \Delta t = \Delta m, \\ \rho A_2 s_2 &= \rho A_2 v_2 \Delta t = \Delta m. \end{align} }[/math]

The work done by the forces consists of two parts:

• The work done by the pressure acting on the areas A₁ and A₂ [math]\displaystyle{ W_\text{pressure}=F_{1,\text{pressure}} s_{1} - F_{2,\text{pressure}} s_2 =p_1 A_1 s_1 - p_2 A_2 s_2 = \Delta m \frac{p_1}{\rho} - \Delta m \frac{p_2}{\rho}. }[/math]
• The work done by gravity: the gravitational potential energy in the volume A₁s₁ is lost, and at the outflow in the volume A₂s₂ is gained. So, the change in gravitational potential energy ΔE_pot,gravity in the time interval Δt is

[math]\displaystyle{ \Delta E_\text{pot,gravity} = \Delta m\, g z_2 - \Delta m\, g z_1. }[/math] Now, the work by the force of gravity is opposite to the change in potential energy, W_gravity = −ΔE_pot,gravity: while the force of gravity is in the negative z-direction, the work—gravity force times change in elevation—will be negative for a positive elevation change Δz = z₂ − z₁, while the corresponding potential energy change is positive. So: [math]\displaystyle{ W_\text{gravity} = -\Delta E_\text{pot,gravity} = \Delta m\, g z_1 - \Delta m\, g z_2. }[/math] And therefore the total work done in this time interval Δt is [math]\displaystyle{ W = W_\text{pressure} + W_\text{gravity}. }[/math] The increase in kinetic energy is [math]\displaystyle{ \Delta E_\text{kin} = \tfrac12 \Delta m\, v_2^2-\tfrac12 \Delta m\, v_1^2. }[/math] Putting these together, the work-kinetic energy theorem W = ΔE_kin gives: [math]\displaystyle{ \Delta m \frac{p_1}{\rho} - \Delta m \frac{p_2}{\rho} + \Delta m\, g z_1 - \Delta m\, g z_2 = \tfrac12 \Delta m\, v_2^2 - \tfrac12 \Delta m\, v_1^2 }[/math] or [math]\displaystyle{ \tfrac12 \Delta m\, v_1^2 + \Delta m\, g z_1 + \Delta m \frac{p_1}{\rho} = \tfrac12 \Delta m\, v_2^2 + \Delta m\, g z_2 + \Delta m \frac{p_2}{\rho}. }[/math] After dividing by the mass Δm = ρA₁v₁ Δt = ρA₂v₂ Δt the result is: [math]\displaystyle{ \tfrac12 v_1^2 +g z_1 + \frac{p_1}{\rho}=\tfrac12 v_2^2 +g z_2 + \frac{p_2}{\rho} }[/math] or, as stated in the first paragraph:

[math]\displaystyle{ \frac{v^2}{2}+g z+\frac{p}{\rho} = C }[/math]

(Eqn. 1, Which is also Equation (A))

Further division by g produces the following equation. Note that each term can be described in the length dimension (such as meters). This is the head equation derived from Bernoulli's principle:

[math]\displaystyle{ \frac{v^2}{2 g}+z+\frac{p}{\rho g}=C }[/math]

(Eqn. 2a)

The middle term, z, represents the potential energy of the fluid due to its elevation with respect to a reference plane. Now, z is called the elevation head and given the designation z_elevation.

A free falling mass from an elevation z > 0 (in a vacuum) will reach a speed [math]\displaystyle{ v = \sqrt{ {2 g}{z} }, }[/math] when arriving at elevation z = 0. Or when rearranged as head: [math]\displaystyle{ h_v =\frac{v^2}{2 g} }[/math] The term v²/2g is called the velocity head, expressed as a length measurement. It represents the internal energy of the fluid due to its motion.

The hydrostatic pressure p is defined as [math]\displaystyle{ p = p_0 - \rho g z , }[/math] with p₀ some reference pressure, or when rearranged as head: [math]\displaystyle{ \psi = \frac{p}{\rho g}. }[/math] The term p/ρg is also called the pressure head, expressed as a length measurement. It represents the internal energy of the fluid due to the pressure exerted on the container. The head due to the flow speed and the head due to static pressure combined with the elevation above a reference plane, a simple relationship useful for incompressible fluids using the velocity head, elevation head, and pressure head is obtained.

[math]\displaystyle{ h_{v} + z_\text{elevation} + \psi = C }[/math]

(Eqn. 2b)

If Eqn. 1 is multiplied by the density of the fluid, an equation with three pressure terms is obtained:

[math]\displaystyle{ \frac{\rho v^2}{2}+ \rho g z + p = C }[/math]

(Eqn. 3)

Note that the pressure of the system is constant in this form of the Bernoulli equation. If the static pressure of the system (the third term) increases, and if the pressure due to elevation (the middle term) is constant, then the dynamic pressure (the first term) must have decreased. In other words, if the speed of a fluid decreases and it is not due to an elevation difference, it must be due to an increase in the static pressure that is resisting the flow.

All three equations are merely simplified versions of an energy balance on a system.

Bernoulli equation for compressible fluids

The derivation for compressible fluids is similar. Again, the derivation depends upon (1) conservation of mass, and (2) conservation of energy. Conservation of mass implies that in the above figure, in the interval of time Δt, the amount of mass passing through the boundary defined by the area A₁ is equal to the amount of mass passing outwards through the boundary defined by the area A₂: [math]\displaystyle{ 0= \Delta M_1 - \Delta M_2 = \rho_1 A_1 v_1 \, \Delta t - \rho_2 A_2 v_2 \, \Delta t. }[/math] Conservation of energy is applied in a similar manner: It is assumed that the change in energy of the volume of the streamtube bounded by A₁ and A₂ is due entirely to energy entering or leaving through one or the other of these two boundaries. Clearly, in a more complicated situation such as a fluid flow coupled with radiation, such conditions are not met. Nevertheless, assuming this to be the case and assuming the flow is steady so that the net change in the energy is zero, [math]\displaystyle{ \Delta E_1 - \Delta E_2 = 0 }[/math] where ΔE₁ and ΔE₂ are the energy entering through A₁ and leaving through A₂, respectively. The energy entering through A₁ is the sum of the kinetic energy entering, the energy entering in the form of potential gravitational energy of the fluid, the fluid thermodynamic internal energy per unit of mass (ε₁) entering, and the energy entering in the form of mechanical p dV work: [math]\displaystyle{ \Delta E_1 = \left(\tfrac12 \rho_1 v_1^2 + \Psi_1 \rho_1 + \varepsilon_1 \rho_1 + p_1 \right) A_1 v_1 \, \Delta t }[/math] where Ψ = gz is a force potential due to the Earth's gravity, g is acceleration due to gravity, and z is elevation above a reference plane. A similar expression for ΔE₂ may easily be constructed. So now setting 0 = ΔE₁ − ΔE₂: [math]\displaystyle{ 0 = \left(\tfrac12 \rho_1 v_1^2+ \Psi_1 \rho_1 + \varepsilon_1 \rho_1 + p_1 \right) A_1 v_1 \, \Delta t - \left(\tfrac12 \rho_2 v_2^2 + \Psi_2 \rho_2 + \varepsilon_2 \rho_2 + p_2 \right) A_2 v_2 \, \Delta t }[/math] which can be rewritten as: [math]\displaystyle{ 0 = \left(\tfrac12 v_1^2 + \Psi_1 + \varepsilon_1 + \frac{p_1}{\rho_1} \right) \rho_1 A_1 v_1 \, \Delta t - \left(\tfrac12 v_2^2 + \Psi_2 + \varepsilon_2 + \frac{p_2}{\rho_2} \right) \rho_2 A_2 v_2 \, \Delta t }[/math] Now, using the previously-obtained result from conservation of mass, this may be simplified to obtain [math]\displaystyle{ \tfrac12 v^2 + \Psi + \varepsilon + \frac{p}{\rho} = \text{constant} \equiv b }[/math] which is the Bernoulli equation for compressible flow.

An equivalent expression can be written in terms of fluid enthalpy (h): [math]\displaystyle{ \tfrac{1}{2} v^2 + \Psi + h = \text{constant} \equiv b }[/math]

Applications

Condensation visible over the upper surface of an Airbus A340 wing caused by the fall in temperature accompanying the fall in pressure.

In modern everyday life there are many observations that can be successfully explained by application of Bernoulli's principle, even though no real fluid is entirely inviscid, and a small viscosity often has a large effect on the flow.

• Bernoulli's principle can be used to calculate the lift force on an airfoil, if the behaviour of the fluid flow in the vicinity of the foil is known. For example, if the air flowing past the top surface of an aircraft wing is moving faster than the air flowing past the bottom surface, then Bernoulli's principle implies that the pressure on the surfaces of the wing will be lower above than below. This pressure difference results in an upwards lifting force. Whenever the distribution of speed past the top and bottom surfaces of a wing is known, the lift forces can be calculated (to a good approximation) using Bernoulli's equations, which were established by Bernoulli over a century before the first man-made wings were used for the purpose of flight.

• The carburetor used in many reciprocating engines contains a venturi to create a region of low pressure to draw fuel into the carburetor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli's principle; in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.
• An injector on a steam locomotive or a static boiler.
• The pitot tube and static port on an aircraft are used to determine the airspeed of the aircraft. These two devices are connected to the airspeed indicator, which determines the dynamic pressure of the airflow past the aircraft. Bernoulli's principle is used to calibrate the airspeed indicator so that it displays the indicated airspeed appropriate to the dynamic pressure.
• A De Laval nozzle utilizes Bernoulli's principle to create a force by turning pressure energy generated by the combustion of propellants into velocity. This then generates thrust by way of Newton's third law of motion.
• The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate, which can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, the continuity equation shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid flow speed. Subsequently, Bernoulli's principle then shows that there must be a decrease in the pressure in the reduced diameter region. This phenomenon is known as the Venturi effect.
• The maximum possible drain rate for a tank with a hole or tap at the base can be calculated directly from Bernoulli's equation and is found to be proportional to the square root of the height of the fluid in the tank. This is Torricelli's law, which is compatible with Bernoulli's principle. Increased viscosity lowers this drain rate; this is reflected in the discharge coefficient, which is a function of the Reynolds number and the shape of the orifice.

• The Bernoulli grip relies on this principle to create a non-contact adhesive force between a surface and the gripper.
• During a cricket match, bowlers continually polish one side of the ball. After some time, one side is quite rough and the other is still smooth. Hence, when the ball is bowled and passes through air, the speed on one side of the ball is faster than on the other, and this results in a pressure difference between the sides; this leads to the ball rotating ("swinging") while travelling through the air, giving advantage to the bowlers.

Misconceptions

Airfoil lift

An illustration of the incorrect equal transit-time explanation of airfoil lift.

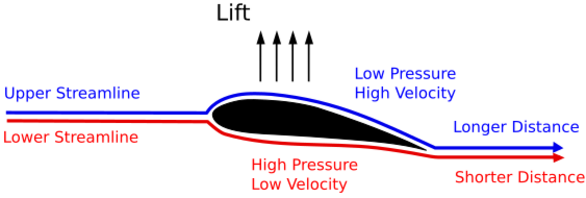
One of the most common erroneous explanations of aerodynamic lift asserts that the air must traverse the upper and lower surfaces of a wing in the same amount of time, implying that since the upper surface presents a longer path the air must be moving over the top of the wing faster than over the bottom. Bernoulli's principle is then cited to conclude that the pressure on top of the wing must be lower than on the bottom.

However, there is no physical principle that requires the air to traverse the upper and lower surfaces in the same amount of time. In fact, theory predicts and experiments confirm that the air traverses the top surface in a shorter time than it traverses the bottom surface, and this explanation based on equal transit time is false. While this explanation is false, it is not the Bernoulli principle that is false, because this principle is well established; Bernoulli's equation is used correctly in common mathematical treatments of aerodynamic lift.

Common classroom demonstrations

There are several common classroom demonstrations that are sometimes incorrectly explained using Bernoulli's principle. One involves holding a piece of paper horizontally so that it droops downward and then blowing over the top of it. As the demonstrator blows over the paper, the paper rises. It is then asserted that this is because "faster moving air has lower pressure".

One problem with this explanation can be seen by blowing along the bottom of the paper: if the deflection was caused by faster moving air, then the paper should deflect downward; but the paper deflects upward regardless of whether the faster moving air is on the top or the bottom. Another problem is that when the air leaves the demonstrator's mouth it has the same pressure as the surrounding air; the air does not have lower pressure just because it is moving; in the demonstration, the static pressure of the air leaving the demonstrator's mouth is equal to the pressure of the surrounding air. A third problem is that it is false to make a connection between the flow on the two sides of the paper using Bernoulli's equation since the air above and below are different flow fields and Bernoulli's principle only applies within a flow field.

As the wording of the principle can change its implications, stating the principle correctly is important. What Bernoulli's principle actually says is that within a flow of constant energy, when fluid flows through a region of lower pressure it speeds up and vice versa. Thus, Bernoulli's principle concerns itself with changes in speed and changes in pressure within a flow field. It cannot be used to compare different flow fields.

A correct explanation of why the paper rises would observe that the plume follows the curve of the paper and that a curved streamline will develop a pressure gradient perpendicular to the direction of flow, with the lower pressure on the inside of the curve. Bernoulli's principle predicts that the decrease in pressure is associated with an increase in speed; in other words, as the air passes over the paper, it speeds up and moves faster than it was moving when it left the demonstrator's mouth. But this is not apparent from the demonstration.

Other common classroom demonstrations, such as blowing between two suspended spheres, inflating a large bag, or suspending a ball in an airstream are sometimes explained in a similarly misleading manner by saying "faster moving air has lower pressure".

See also

• Torricelli's law
• Coandă effect
• Euler equations – for the flow of an inviscid fluid
• Hydraulics – applied fluid mechanics for liquids
• Navier–Stokes equations – for the flow of a viscous fluid
• Teapot effect
• Terminology in fluid dynamics

External links

• The Flow of Dry Water - The Feynman Lectures on Physics
• Science 101 Q: Is It Really Caused by the Bernoulli Effect?
• Bernoulli equation calculator
• Millersville University – Applications of Euler's equation
• NASA – Beginner's guide to aerodynamics
• Misinterpretations of Bernoulli's equation – Weltner and Ingelman-Sundberg